
- •1.1. Атомно-молекулярная теория строения вещества
- •1.2. Масса и размеры молекул
- •1.3. Броуновское движение
- •2. Газовые законы. Идеальный и реальный газы
- •2.1. Законы Бойля-Мариотта, Гей-Люссака, Шарля
- •2.2. Уравнение состояния идеального газа
- •2.3. Плотность газов
- •2.4. Основное уравнение молекулярно-кинетической теории газов
- •2.5. Постоянная Больцмана
- •3.1. Длина свободного пробега молекул
- •3.2. Скорость газовых молекул
- •3.3. Распределение Максвелла
- •4.1. Предмет термодинамики. Постулаты термодинамики
- •4.2. Температурные шкалы. Абсолютная температура
- •4.3. Температура в молекулярно-кинетической теории
- •4.3. Температура в молекулярно-кинетической теории
- •4.4. Внутренняя энергия. Работа. Теплота
- •4.5. Первое начало термодинамики.Понятие теплоемкости
- •4.6. Применение первого начала термодинамики к описанию изопроцессов в идеальном газе
- •4.7. Первое начало термодинамики как принцип эквивалентности теплоты и работы
- •4.8. Невозможность вечного двигателя первого рода
- •4.9. Принципы работы тепловых машин
- •4.10. Цикл карно. Кпд тепловых двигателей
- •4.11. Обратимые и необратимые процессы
- •4.12. Второй закон термодинамики
- •4.13. Теорема карно
- •4.14. Энтропия. Неравенство клаузиуса. Математическое выражение второго начала термодинамики
- •4.15. Статистический смысл второго начала термодинамики
- •4.16. Энтропия и термодинамическая вероятность. Формула больцмана
- •4.17. Энтропия и беспорядок
- •4.18. О "тепловой смерти" вселенной
- •5.1. Кристаллическая решетка
- •5.2. Дефекты в кристаллах
- •5.3. Плавление и кристаллизация
- •5.4. Зависимость температуры плавления от давления
- •5.5. Испарение твердых тел (сублимация)
- •5.6. Механические свойства твердых тел
- •6.1. Силы взаимодействия между молекулами. Агрегатные состояния вещества
- •6.2. Особенности строения и теплового движения в жидкостях
- •6.3. Свойства жидкостей
- •6.4. Явления на границе жидкость–пар. Насыщенный пар
- •6.5. Кипение жидкости. Зависимость температуры кипения от давления
- •6.6. Равновесие двухфазного состояния жидкость-пар. Критическая температура
- •6.7. Водяной пар в атмосфере. Влажность
- •6.8. Поверхностное натяжение
- •6.9. Давление Лапласа под искривленной поверхностью жидкости
- •6.10. Капиллярные явления. Формула Жюрена
- •6.11. Смачивание и несмачивание на границе жидкость-жидкость и твердое тело-жидкость
- •6.12. Текучесть жидкости. Сверхтекучесть гелия
6.2. Особенности строения и теплового движения в жидкостях
По внутренней структуре жидкость занимает промежуточное место между газами и твердыми телами. Исследования, проведенные в последнее время, свидетельствуют, что жидкость по своему строению скорее ближе к кристаллу, чем к газу. На это указывает количественная близость плотностей, удельных теплоемкостей, коэффициентов объемного расширения жидкостей и кристаллов. Сравнение теплоты плавления и парообразования показывает, что последняя в 30-40 раз больше теплоты плавления.
На основании изучения рассеяния рентгеновских лучей, нейтронов и электронов установлено, что жидкость обладает своеобразной молекулярной структурой: ближайшие соседи каждой молекулы жидкости располагаются в определенном порядке, так что число ближайших соседей и их взаимное расположение в среднем для всех молекул одинаковы, то есть в жидкости существует так называемый ближний порядок. Таким образом, ближний порядок заключается в упорядоченном расположении около произвольно выбранной молекулы некоторого числа ее ближайших соседей.
Структура жидкости и ее физические свойства описываются набором функций распределения, устанавливающих вероятностную связь между взаимным расположением молекул. Наибольшее значение имеет радиальная функция распределения G(r). Эта функция определяет число частиц, находящихся в шаровом слое толщиной Δr на расстоянии r от произвольно выбранной (центральной) частицы. Число таких частиц определяется равенством
|
(6.2) |
|
|
|
|
|
Состояние жидкости, как и любой другой термодинамической системы, может быть описано уравнением состояния. Однако вид этого уравнения получен только для некоторых частных случаев, например, для простых жидкостей, состоящих из сферически симметричных молекул, в предположении, что взаимодействие между молекулами носит парный характер и осуществляется центральными силами. Вид уравнения состояния жидкостей зависит от вида функций G(r) и U(r) (потенциальная энергия взаимодействия молекул), для нахождения которых разработан ряд теоретических методов.
Многие особенности поведения жидкости обусловлены весьма сложным характером теплового движения ее молекул. Для жидкости характерно существование различных типов движения: поступательные перемещения молекул, вращения молекул, колебания молекул в поле соседних молекул, колебания атомов внутри отдельных молекул. Сложность заключается в том, что все эти типы движений нельзя, строго говоря, рассматривать порознь в "чистом виде", поскольку существует сильное взаимное влияние движений.
Существуют разные модели, в которых
делаются попытки совместить указанные
виды движений. К числу таких моделей
относится "модель диффузии скачком".
Согласно этой модели молекулы жидкости
совершают тепловые колебания около
положения равновесия со средней частотой
![]() ,
близкой к частотам колебания атомов в
кристаллах, и амплитудой, определяемой
свободным объемом, предоставляемом
молекуле ее соседями. Изредка по сравнению
с периодом колебания около положения
равновесия, по истечении времени
,
близкой к частотам колебания атомов в
кристаллах, и амплитудой, определяемой
свободным объемом, предоставляемом
молекуле ее соседями. Изредка по сравнению
с периодом колебания около положения
равновесия, по истечении времени
![]() ,
эти положения равновесия смещаются на
расстояние порядка 10-8 см. В
привычном нам масштабе времени за одну
секунду молекула в жидкости может менять
свое положение миллиарды раз.
,
эти положения равновесия смещаются на
расстояние порядка 10-8 см. В
привычном нам масштабе времени за одну
секунду молекула в жидкости может менять
свое положение миллиарды раз.
Перемещение молекулы из одного равновесного положения в другое совершается не непрерывно, а в виде активированных скачков с преодолением потенциального барьера высотой W (энергия активации). Эту энергию молекула может получить в процессе взаимодействия с другими молекулами. Установлено, что с повышением температуры продолжительность среднего (по совокупности большого числа молекул) времени оседлой жизни молекулы быстро уменьшается, подчиняясь экспоненциальному закону:
|
(6.3) |
где k – константа Больцмана.
Время
![]() является
характерным временем, связанным с
перемещением частиц жидкости на
расстояние δ, по порядку величины равное
среднему расстоянию между молекулами.
Экспериментально установлено, что
является
характерным временем, связанным с
перемещением частиц жидкости на
расстояние δ, по порядку величины равное
среднему расстоянию между молекулами.
Экспериментально установлено, что
|
(6.4) |
где μ – молекулярный вес жидкости, ρ –
ее плотность, NA – число
Авогадро. Для воды, например,
![]() .
.
Нетрудно видеть, что время
определяет
среднюю скорость
![]() теплового
движения молекул жидкости:
теплового
движения молекул жидкости:
|
(6.5) |
Существует также другая модель теплового движения в жидкости, согласно которой молекула ведет себя следующим образом: она совершает колебания в окружении своих соседей, а само это окружение плавно перемещается в пространстве ("плывет") и при этом постепенно деформируется. Такая модель теплового движения в жидкости называется "моделью непрерывной диффузии".

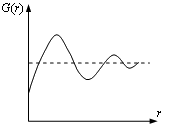 Рис.
6.2
Рис.
6.2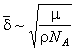 ,
,