1. Определение перпендикулярности прямой и плоскости

2. Признак перпендикулярности прямой и плоскости.

Определение. Прямая, пересекающая плоскость называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой лежащей на плоскости и проходящей через точку пересечения данной прямой и плоскости.

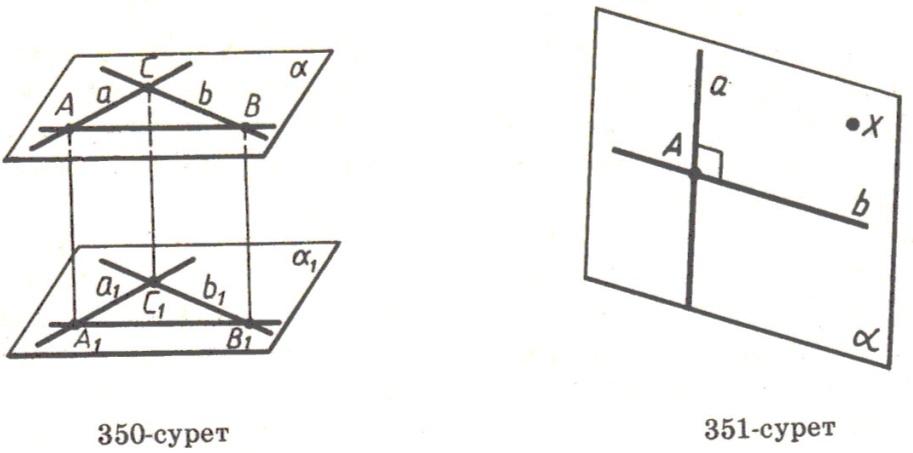
Признак перпендикулярности прямой и плоскости.

Теорема. Если прямая, пересекающая плоскость перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения, то она перпендикулярна плоскости.

Дано:

плоскость α

всα

ссα

ав ас

вηс=А Доказать: аα

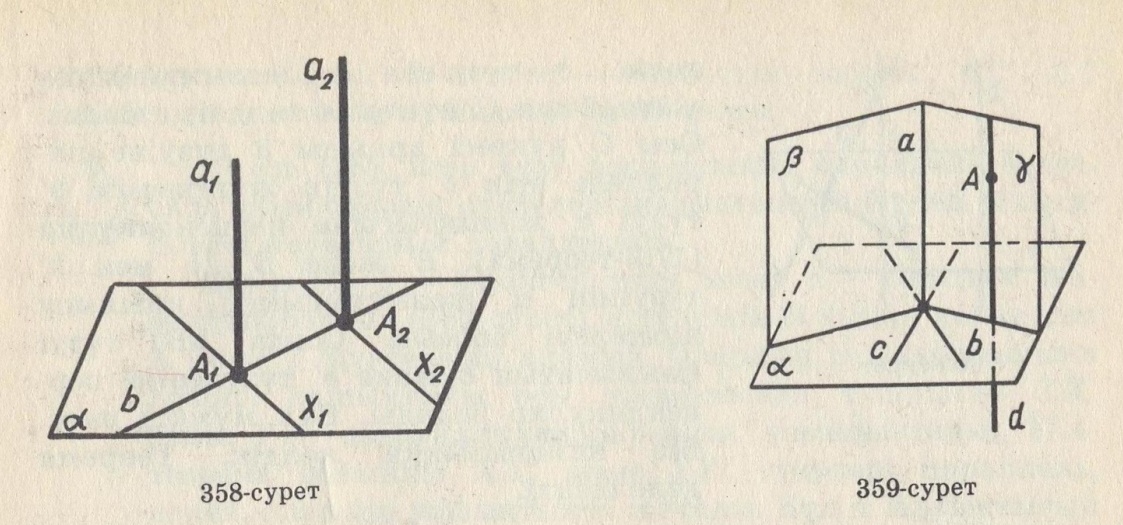
Доказательство:

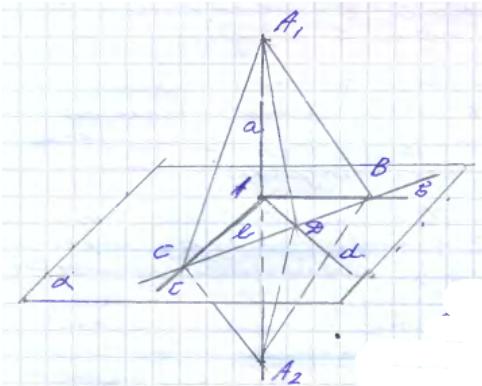
Проведем: АА₁=АА₂, dсαℓηс=С

ℓηв=βℓηd=D, если докажем аd, то аα.

Рассмотрим:

1) ∆А₁СА₂ – равнобедренный (АС-медиана, высота)→А₁С=А₂С

2) ∆А₁ВА – равнобедренный (АВ-медиана, высота)→ А₁В=А₂В

3) ∆А₁ВС=∆А₂ВС (по III признаку)→А₁ВС=А₂ВС

4) ∆А₁ВД=∆А₂ВД (по I признаку)→ А₁Д=А₂Д

5) ∆А₁ДА=∆А₂ДА (по III признаку)→А₁АД=А₂АД

но эти углы смежные →А₁АД=А₂АД=90⁰→А₁Аd→А₁Аα

Домашнее задание.

1) Выучит по конспекту доказательство признака перпендикулярности прямой и плоскости.

2) Задача. АВСД – ромб в плоскости α. О – точка пересечения диагоналей ромба. Прямая d перпендикулярна к плоскости α и проходит через точку О. Е – точка прямой d. Найти расстояние от точки Е до вершины ромба, если |ОЕ|=8см, |АВ|=12см, один из углов ромба равен 60⁰. (Ответ. 10см., )

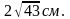3) Задача. ∆АВС – равносторонний |АВ|=3см. Из вершины А восстановлен перпендикуляр. |АО|=4см. Найти площадь ∆ОВС. (Ответ. )

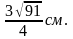Урок № 60. Тема 6.6: Перпендикуляр и наклонные. Угол между прямой и плоскостью. Теорема о трех перпендикулярах.

План занятия.

Признак параллельности прямой и плоскости.

Признак параллельности двух плоскостей.

Признаке перпендикулярности прямой и плоскости.

б) Дать определение угла между прямой и плоскостью

Задача. Из точки отстоящей от плоскости на расстоянии 12 см. проведены две наклонные образующие с плоскостью углы 30⁰, а между собой угол 90⁰. Определить расстояние между концами наклонных. (Ответ. )

в) Доказать теорему о трех перпендикулярах.

Теорема. Прямая проведенная на плоскости через основание наклонной перпендикулярной к проекции наклонной перпендикуляра к самой наклонной.

Д ано:

Плоскость α

АВ – наклонная

ВСα

аСα

аВС

Доказать: аАВ

Доказательство:

ВСа или аВС (1) АСа или аАС (2)

из условий (1) и (2)→аβ→аАВ

Обратная теорема. Прямая проведенная на плоскости через основание наклонной перпендикулярно наклонной, перпендикулярна проекции наклонной.

Задача. Из вершины А прямоугольника АВСД к его плоскости проведен перпендикуляр АК конец которого отстает от других вершин на расстоянии 6 см, 7см, 9 см. Найти |АК|.

(Ответ. 2 см.).

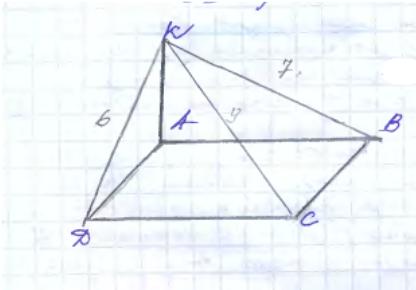∆ КВС:|ВС|=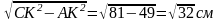

АД=ВС=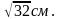

∆АДК:|АК|=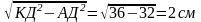

|АК|=2см.

Домашнее задание

1) Доказать теорему о 3-х перпендикулярах.

2) Задача. Из точки отстоящей от плоскости на расстояние 10 см проведены две наклонные образующие с плоскостью углы в 45⁰, а между собой угол в 60⁰. Определить расстояние между концами наклонных. (Ответ. ).

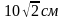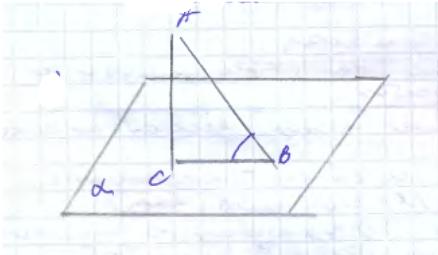
Дано:

АВ – наклонная равна 20 см.

α=30⁰, 45⁰, 60⁰

Найти ВС. (3 случая).

Занятие 62.