
- •Формулы нахождения производных показательной функции.
- •Решение упражнений.
- •Решение упражнений
- •Определение максимума
- •Определение минимума.
- •Признаки максимума и минимума.
- •1.Наибольшее, наименьшее значения функции на промежутке.
- •2.Задачи на максимум, минимум функции.
- •1.Дифференциал функции и его геометрический смысл.
- •2. Применения дифференциала в приближенных вычислениях.
- •Решение упражнений.
- •Решение упражнений.
- •Контрольная работа.
- •Домашняя работа.
- •Раздел VI. Прямые и плоскости в пространстве.
- •Определение перпендикулярности прямой и плоскости
- •Признак перпендикулярности прямой и плоскости.
- •Тема 6.7. : Двугранный угол. Перпендикулярность двух плоскостей.
- •1. Организация занятия.
- •2. Проверка домашнего задания.
- •Разложение вектора по координатным осям
- •Прямоугольные координаты на плоскости и пространстве.
- •Действия над векторами, заданными своими координатами.
- •Длина вектора, угол между векторами.
- •Неопределенный интеграл
- •Свойства неопределенного интеграла.
- •Непосредственное интегрирование.
- •Площадь криволинейной трапеции.
- •Определенный интеграл
- •Свойства определенного интеграла.
- •Вычисление определенного интеграла.
- •Тема 9.4.: Решение задач.
- •3. Решение задачи
- •Тема 9.6.: Осевые сечения цилиндра, конуса, усеченного конуса.
- •Осевые сечения цилиндра.
- •Осевые сечения конуса.
- •Осевые сечения усеченного конуса.
- •Тема 9.7.: Шар, сфера. Поверхность сферы.
- •Тема 10.1.: Объем призмы.
- •Тема 10.2: Объем пирамиды, объем усеченной пирамиды.
- •Тема 10.3.: Решение задач.
- •Тема 10.4.: Объем цилиндра.
- •Тема 10.6: Объем конуса, усеченного конуса.
- •Формула нахождения объема конуса, усеченного конуса.
- •Решение задач на применение формул.
- •Формула нахождения объема шара.
- •Решение задач
- •2.Элементы комбинаторики
- •Теоремы сложения и умножения вероятностей
- •Решение задач.
- •Случайные величины
- •Закон распределения дискретной случайной величины
- •Биноминальное распределение
- •Закон распределения дискретной случайной величины
- •Биноминальное распределение
- •Числовые характеристики дискретных случайных величин
- •Определение дисперсии.
- •2. Свойства математического ожидания
- •Вычисление дисперсии
- •Свойства дисперсии
- •Среднее квадратическое отклонение
Урок № 41. Тема 5.6. Производная сложной функции.
План.
Вывод формулы нахождения производной сложной функции.
Решение примеров.
Рассмотрим функцию
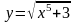 тогда
тогда
В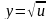 озьмем
еще функцию
озьмем
еще функцию
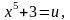
О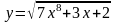
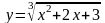
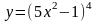
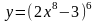
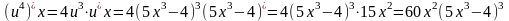
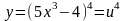
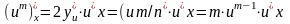
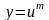
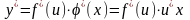
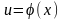
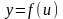 бозначим
тогда - сложная функция
бозначим
тогда - сложная функция
Пусть
Производная данной функции находится по формуле:
Рассмотрим сложную степенную функцию
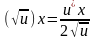
Р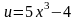 ассмотрим
ассмотрим
1)
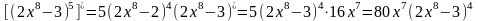
2)
u
Решить :
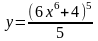
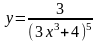
1) 2) 3)
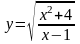
4) 5) 6)
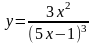
7)
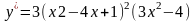
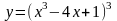 Домашнее
задание
Домашнее
задание
1)
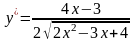
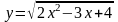
2)
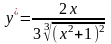
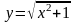
3)
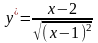
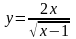
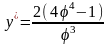
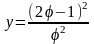
4)
5)
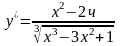
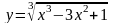
6)
Урок 43. Тема 5.7. Производная степенной функции с натуральным показателем. Производная синуса и косинуса.
План.
Производная степенной функции с натуральным показателем.
Производная тригонометрических функций.
Вывести формулы производных
у=С, у=х,…у=хn n – любое рациональное.
Найти производные функций
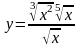
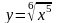
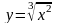
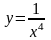
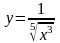 ;
2) 3) 4) 5)
;
2) 3) 4) 5)
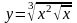
6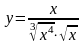 )
7)
)
7)
Найти производные функций
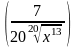
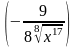
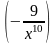
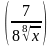
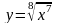
1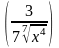 )
2)
)
2)
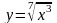
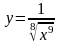
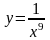
3) 4)
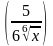
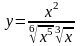
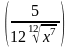
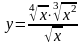
5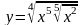 )
6)
)
6)
7)
Определение производной, последовательность нахождения ее.
Найти (sin x)/
1)
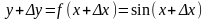
2)
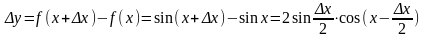
3)
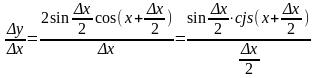
4)
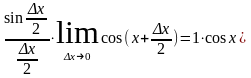
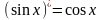
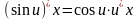
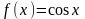
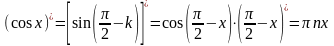
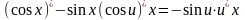
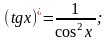
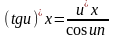
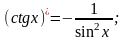
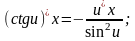
Решение упражнений:
Найти у/, если:
1.
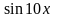 7.
7.
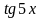 13.
13.
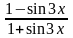
2.
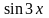 8.
8.
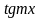 14.
14.
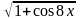
3.
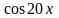 9.
9.
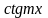 15.
15.
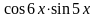
4.
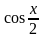 10.
10.
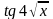 16.
16.
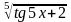
5.
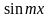 11.
11.
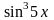
6.
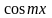 12.
12.
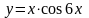
Контрольные вопросы:
Какая функция называется степенной?
По какой формуле находится производная степенной функции?
Какие тригонометрические функции вы знаете?
По какой формуле находится производная синуса и косинуса?
Нахождение производной называется?
Урок № 44. Тема 5.8. Производная показательной функции.
План.
Формулы нахождения производных показательной функции.
Решение упражнений.
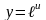
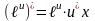
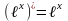
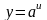
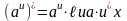
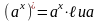
Найти производные функций
1)
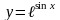 5)
5)
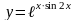 8)
8)
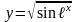
2)
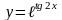 6)
6)
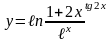 9)
9)
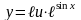
3)
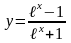 7)
7)
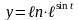
4)
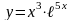
Домашнее задание
Найти у/, если:
1)
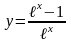
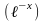
2)
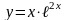
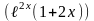
3)
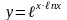
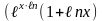
4)
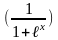
5)
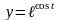
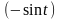
6)
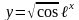
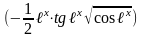
7)
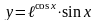
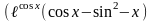
8)
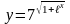
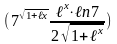
Урок № 45 .Тема 5.9. Производная логарифмических функций.
План.
Повторение определение логарифма, свойств.
Формулы нахождения производной логарифма.
Решение упражнений.
Рассмотрим
предел вычисления
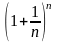 при
n→∞. Предел
при
n→∞ равный приближенно 2,718, принято
обозначать буквой ℓ и это записывается
при
n→∞. Предел
при
n→∞ равный приближенно 2,718, принято
обозначать буквой ℓ и это записывается
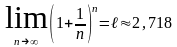
Определение: Логарифмы по основанию ℓ называются натуральными.
Натуральный логарифм числа N обозначается ℓnN. Между десятичным и натуральным логарифмами числа N существуют зависимости:
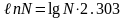
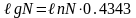
Рассмотрим формулы дифференцирования логарифмических функций
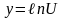
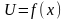
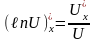
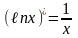
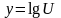
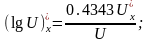
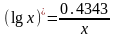
Решить примеры:
1)
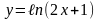 2)
2)
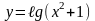
3)
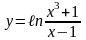 4)
4)
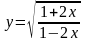
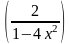
5)
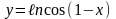 6)
6)
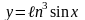 7)
7)
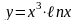
Домашнее задание
Найти у/, если:
1)
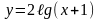
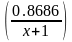
2)
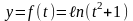
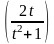
3)
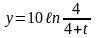
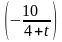
4)
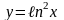
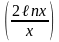
5)
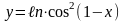
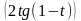
6)
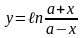
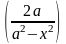
7)
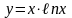
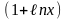
8)
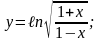
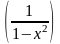
Контрольные вопросы:
Какая функция называется логарифмической функцией?
Какими свойствами обладает логарифмическая функция?
По какой формуле находится производная логарифмической функции?
По какой формуле находится производная натурального логарифма?
По какой формуле находится производная десятичного логарифма?
Урок № 46 (2) Тема 5.10. Производные обратных тригонометрических функций.
План.
Формулы нахождения производных обратно тригонометрических функций.
Решение упражнений
Формулы нахождения производных обратно тригонометрических функций.
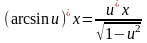
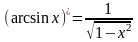

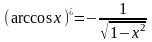
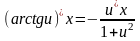
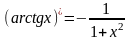

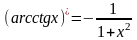
Решить упражнения:
1)
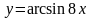 6)
6)
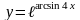
2)
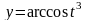 7)
7)
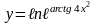
3)
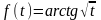 8)
8)
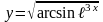
4)
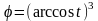 9)
9)
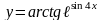
5)
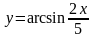
Домашнее задание
а) Повторить все формулы дифференцирования.
б) Найти у/, если:
1)
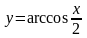
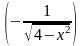
2)
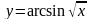
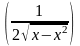
3)
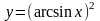
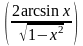
4)
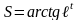
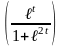
5)
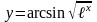
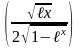
6)
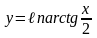
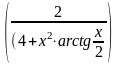
7)
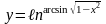
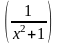
Урок № 48. Тема 5.11. Вторая производная и ее физический смысл.
План.
1.Определение второй производной функции.
2. Механический смысл производной II порядка.
Рассмотрим
функцию
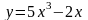
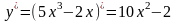 -
I
производная или производная нового
порядка
-
I
производная или производная нового
порядка
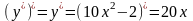 -
II производная или производная второго
порядка
-
II производная или производная второго
порядка
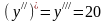 -
III производная или производная третьего
порядка
-
III производная или производная третьего
порядка
Определение: Производная от первой производной, если она существует, называется второй производной или производной II порядка.
Определение: Производная от второй производной, если она существует, называется третьей производной или производной III порядка.
Производная n порядка обозначается у(n)
Механический смысл производной II порядка.
Пусть
тело движется прямолинейно по закону
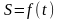 .
Скорость тела в данный момент времени
t определяется как производная пути по
времени
.
Скорость тела в данный момент времени
t определяется как производная пути по
времени
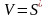 .
.
Если
тело движется неравномерно, то скорость
V c течением времени изменяется и за
промежуток времени ∆t
получает приращение ∆V.
В этом случае отношение
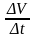 называется
средним
ускорением
в промежутке времени от t
до t+∆t.
называется
средним
ускорением
в промежутке времени от t
до t+∆t.
Положим, что ∆t→0, тогда t+∆t→t а среднее ускорение стремится к величине, которая называется ускорением в данный момент времени t и обозначается j.
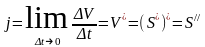
Определение: Ускорением прямолинейного движения тела в данный момент равно второй производной пути по времени, вычисленной для данного момента времени.
Таков механический смысл второй производной.
Задача. Точка движения по закону (прямолинейно)
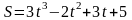 Найти
V и j в момент t=5.
Найти
V и j в момент t=5.
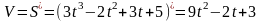

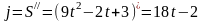
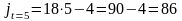
Домашнее задание:
Найти вторые производные функций
1)
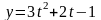 (6)
(6)
2)
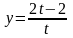
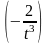
3)
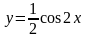
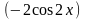
4)
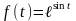
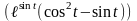
5)
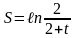
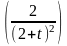
Урок № 49. Тема 5.12. Признаки возрастания, убывания функций.
План.
Признаки возрастания и убывания функции.
Алгоритм определения промежутков возрастания и убывания функции.
Р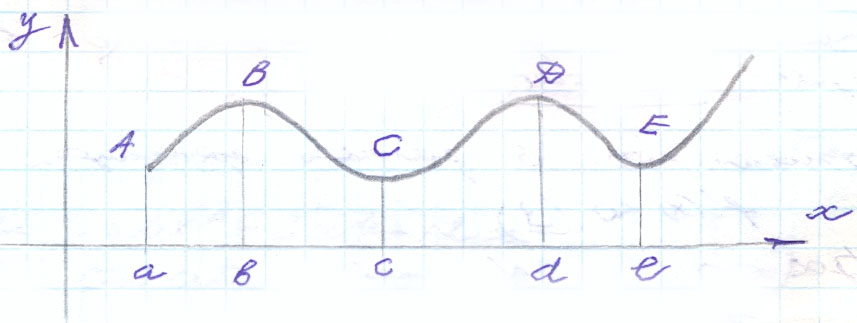 ассмотрим
функцию
ассмотрим
функцию
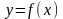 ,
построим ее график
,
построим ее график
В промежутках (α;в), (с;d) функция возрастает, в промежутках (в;с), (d;e) функция убывает.
Признаки возрастания и убывания функции
Теорема. Если производная функции в данном промежутке значений х положительна, то функция возрастает в этом промежутке, если производная отрицательна, то функция убывает.
Поясним данную теорему геометрически.
I Пусть в данном промежутке значений х
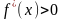 (1)
(1)
то
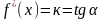 (2)
(2)
где
к – угловой коэффициент касательной
проведенной к графику функции
,
α – угол наклона этой касательной к
положительно направлению оси ох из
равенства (2) следует, что если
то
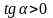 ,
откуда α – острый угол. Отсюда получаем
следующий график функции
,
откуда α – острый угол. Отсюда получаем
следующий график функции
П о
чертежам видно график направлен вверх
и функция возрастает.
о
чертежам видно график направлен вверх
и функция возрастает.
II Предположим, что в данном промежутке
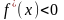 (3)
(3)
тогда
 и α – тупой угол
и α – тупой угол
Получим
П о
чертежам видно что касательные образуют
тупые углы с положительным направлением
ох и график направлен вниз и функция
убывает.
о
чертежам видно что касательные образуют
тупые углы с положительным направлением
ох и график направлен вниз и функция
убывает.
Найти промежутки возрастания, убывания функции
1) Найти область определения функции.
2) Вычислить производную функции.
3) Решить неравенство или .
4) Используя утверждение теоремы найти промежутки возрастания или убывания функции.
Найти промежутки возрастания и убывания функций
1.
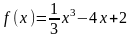
1) D(f)=(-∞;∞)
2)
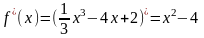
3)
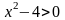
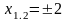

4) Функция на промежутках (-∞; -2] и (2; ∞] – на промежутке [-2; 2] возрастает
[-2; 2] убывает
2.
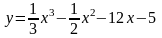
Ответ: (-∞; -3] и (4; ∞] - возрастает
(-3; 4] убывает
Домашнее задание:
Найти промежутки возрастания, убывания функций
1)
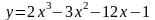
Ответ: (-∞; -1] и (2; ∞] - возрастает
[-1; 2] убывает
2)
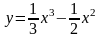
Ответ: (-∞; 0] и (2; +∞] - возрастает
[0; 1] убывает
Контрольные вопросы:
Дать определение возрастающей, убюывающей функции.
Сформулировать условия убывания, возрастания функции.
Сформулировать правила нахождения интервалов монотонности.
Какими точками отделяются промежутки возрастания от промежутков убывания.
Определить интервалы возрастания, убывания функции
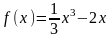
Урок № 50 Тема 5.12. Экстремум функций. Исследование функций на экстремум по первой производной.
План.
