
- •Өзіндік жұмыстар материалдары
- •Жеке тапсырма №1. Тақырыбы: «сызықтық теңдеулер жүйесі ».
- •Бақылау жұмысы №2. Тақырыбы: «векторлық алгебра және аналитикалық геометрия»
- •Жеке тапсырма №4 Тақырыбы: «шектер»
- •Жеке тапсырма №5 Тақырыбы: «функцияның туындысы»
- •Жеке тапсырма №6 Тақырыбы: «бірнеше айнымалылы функция».
- •Жеке тапсырма №7
- •1) Тікелей интегралдау және айнымалыны алмастыру әдісі.
- •2) Интеграл түрі: ;
- •4) Тригонометриялық алмастыруларды келесі мысалға қолдану:
- •5) Рационал бөлшектерді интегралдау:
- •2) Интеграл түрі: ;
- •5) Рационал бөлшектерді интегралдау:
- •2) Интеграл түрі: ;
- •5) Рационал бөлшектерді интегралдау:
- •2) Интеграл түрі: ;
- •5) Рационал бөлшектерді интегралдау:
- •5) Рационал бөлшғктерді интегралдау:
- •2) Интеграл түрі: ;
- •4) Тригонометриялық алмастыруларды келесі мысалға қолдану:
- •5) Рационал бөлшектерді интегралдау:
- •2) Интеграл түрі: ;
- •5) Рационал бөлшектерді интегралдау:
- •2) Интеграл түрі: ;
- •5) Рационал бөлшектерді интегралдау:
- •2) Интеграл түрі: ;
- •5) Рационал бөлшектерді интегралдау:
- •2) Интеграл түрі: ;
- •5) Рационал бөлшектерді интегралдау:
- •Бақылау жұмысы №4 Тақырыбы: «дифференциалдық теңдеулер»
- •Бақылау жұмысы №5 Тақырыбы: «қатарлар».
Жеке тапсырма №5 Тақырыбы: «функцияның туындысы»
Мақсаты: Ақырсыз кіші» және «ақырсыз үлкен шамалар анықтамасын, олардың қасиеттерін оқу.
Тапсырма: Функцияның туындысын табыңыз.
Нұсқа №1, 11




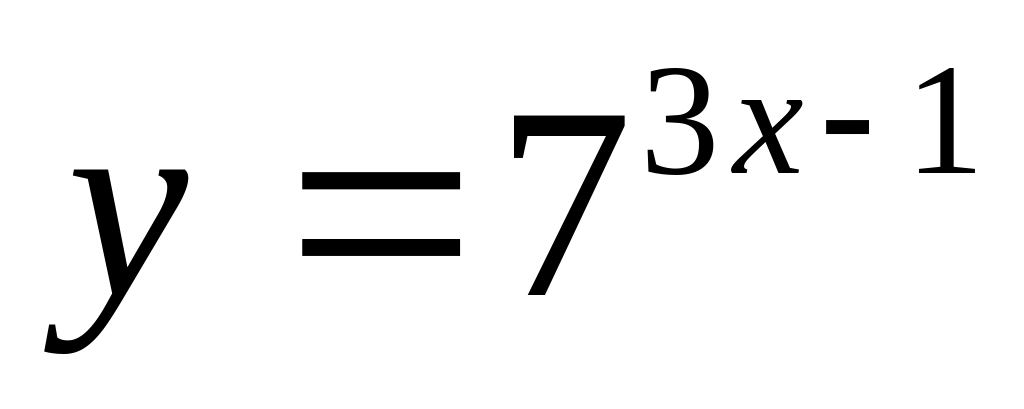


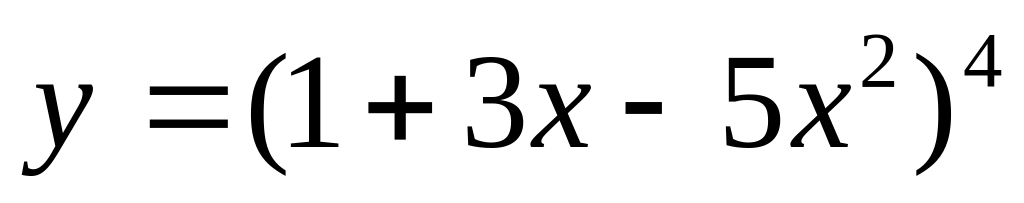
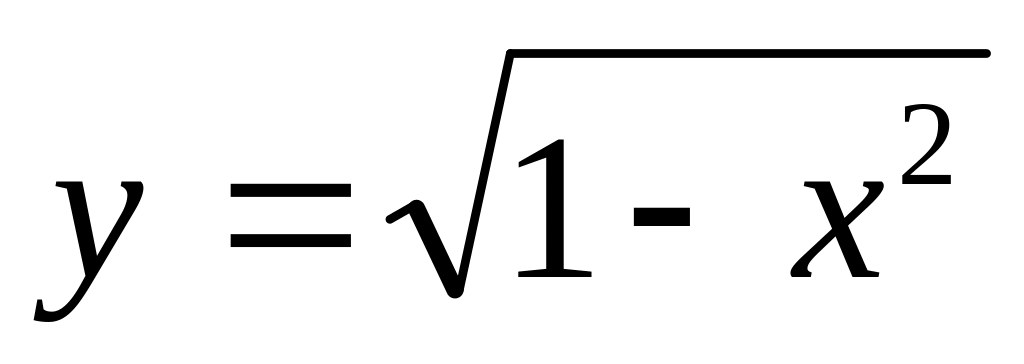



Есептеңіз
 :
: 
Есептеңіз
 :
: 
Есептеңіз
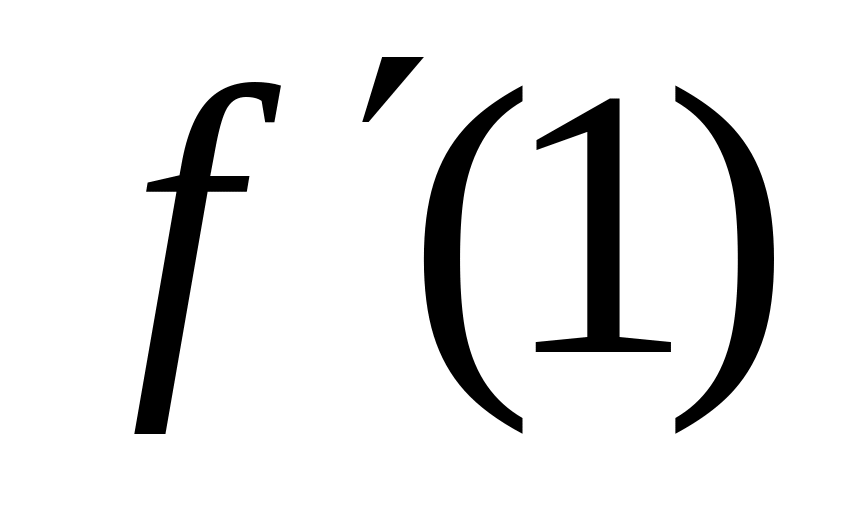 :
: 
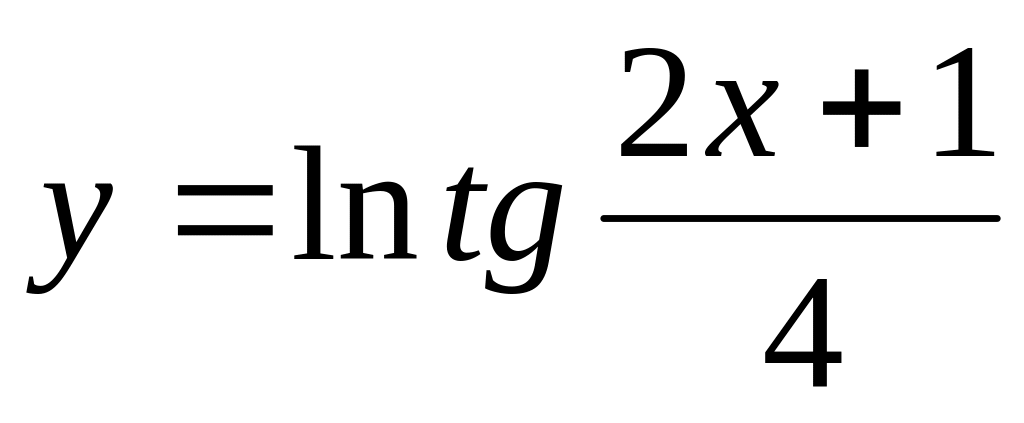


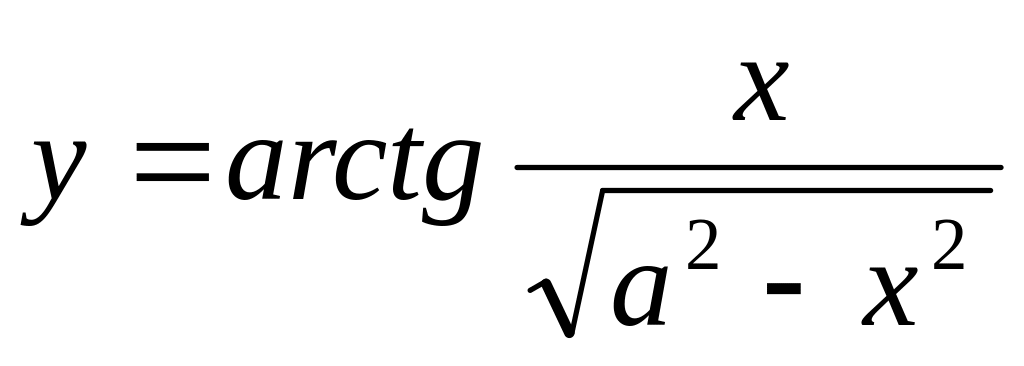
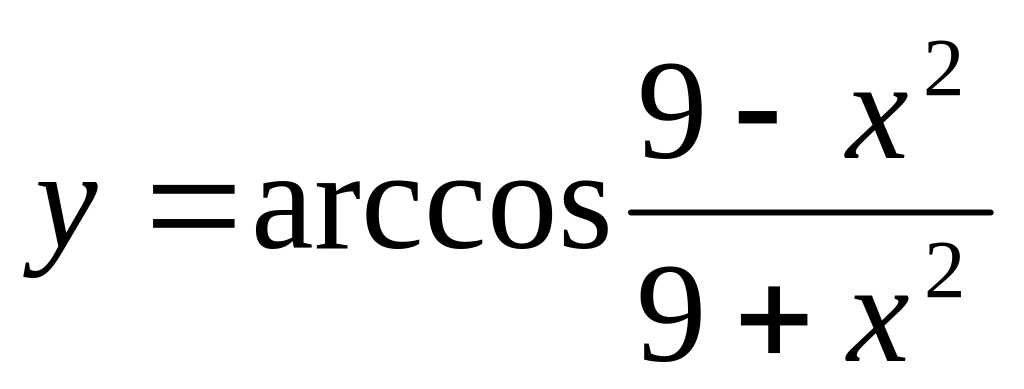
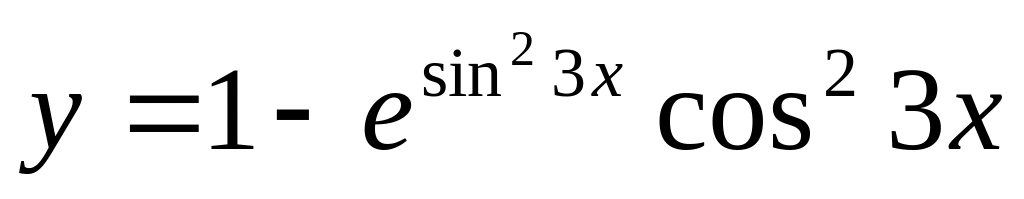
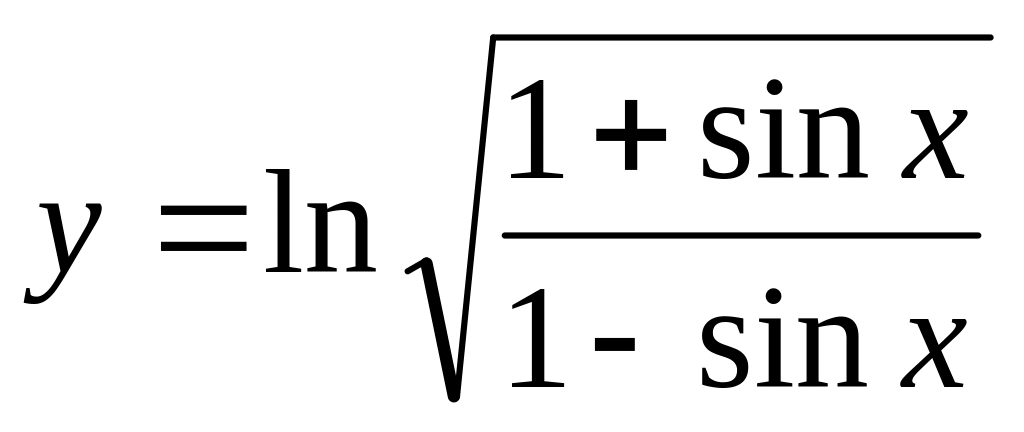



Нұсқа №2, 12


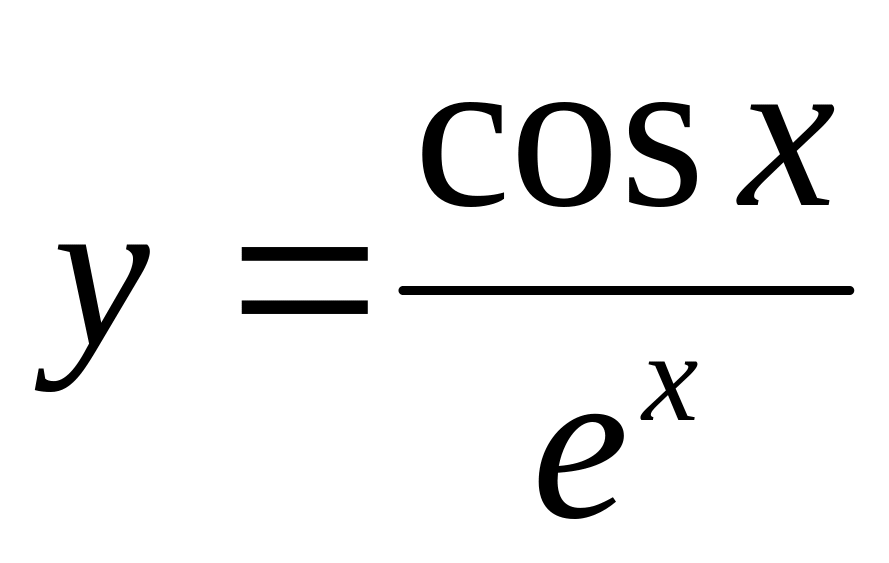
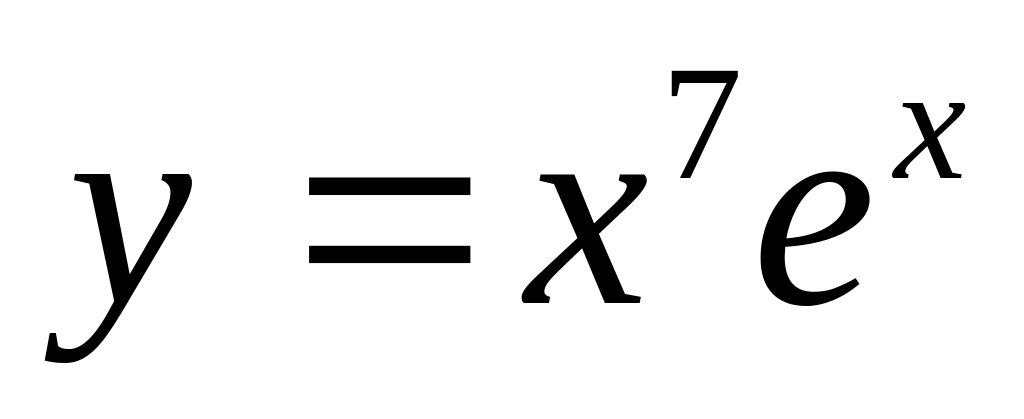





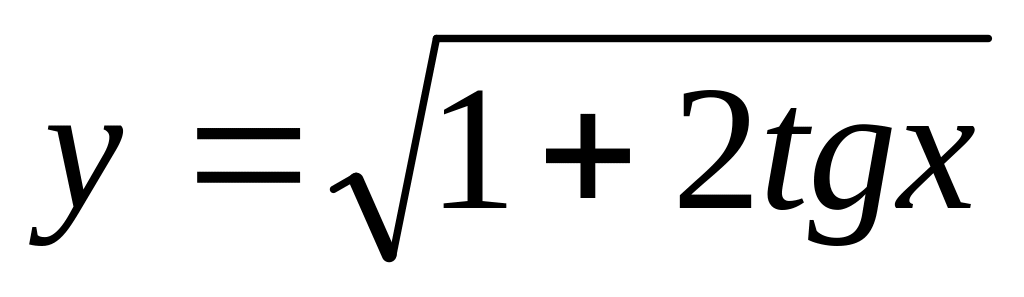
Есептеңіз :
Есептеңіз
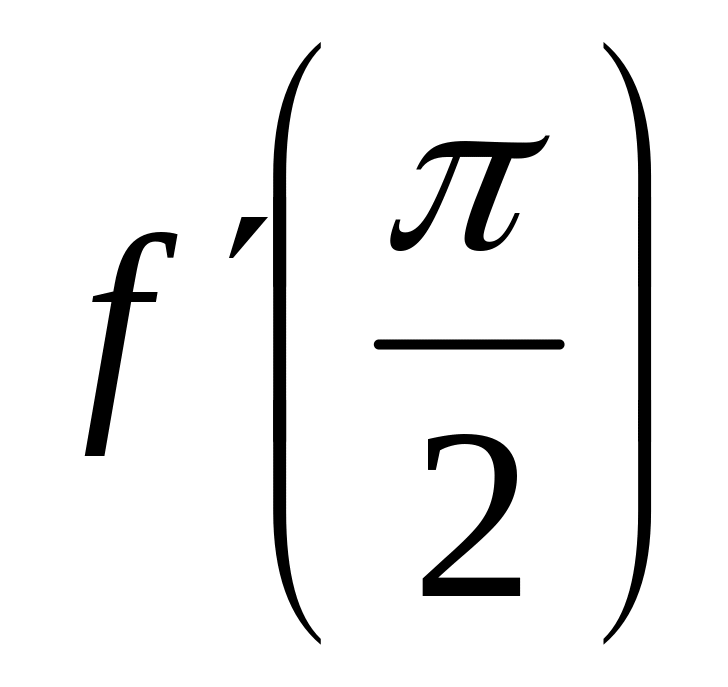 :
: 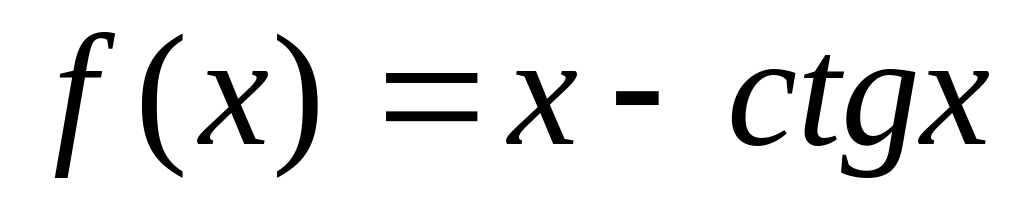
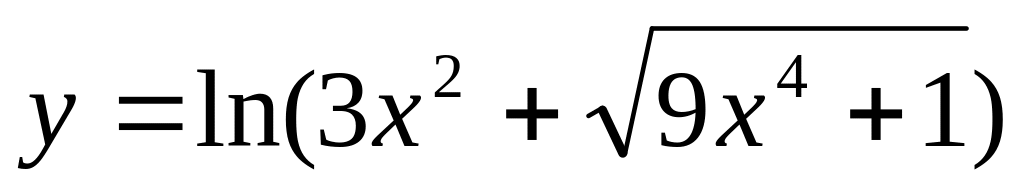
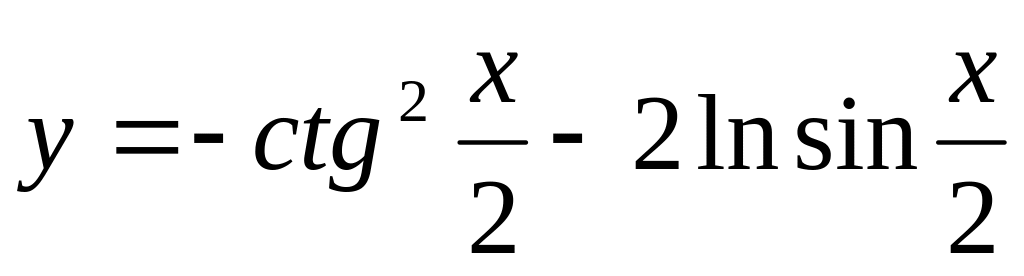






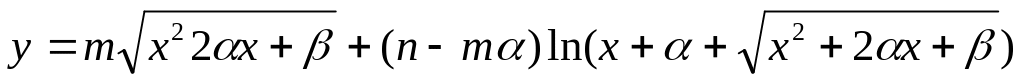
Нұсқа №3, 13







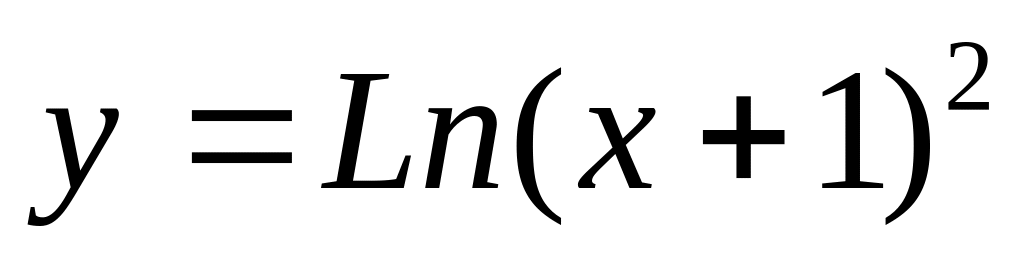

Есептеңіз
 :
: 
Есептеңіз
 :
: 
 ;
;

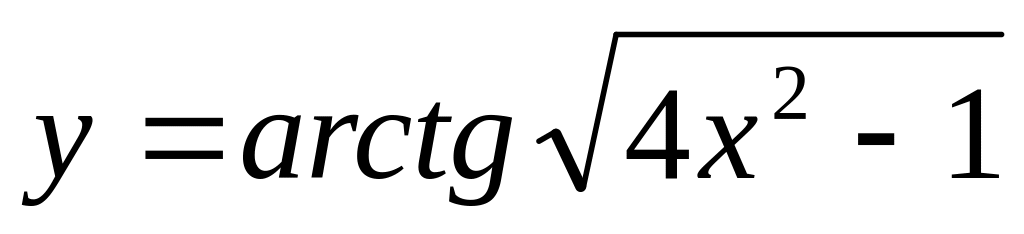

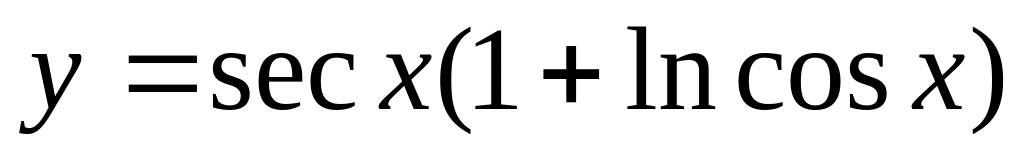 ;
;
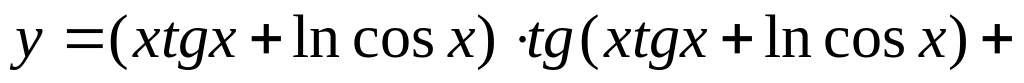
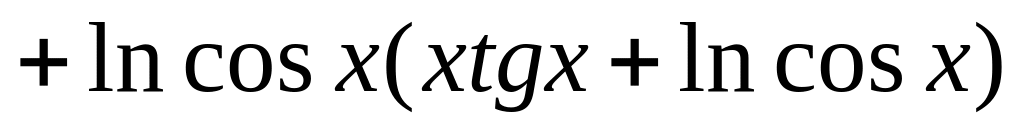
Нұсқа №4, 14



Есептеңіз :
Есептеңіз :


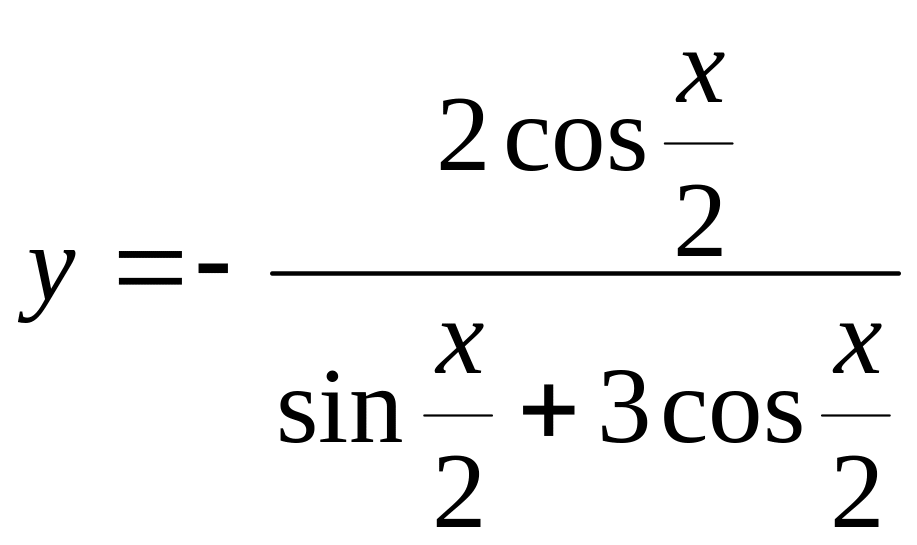

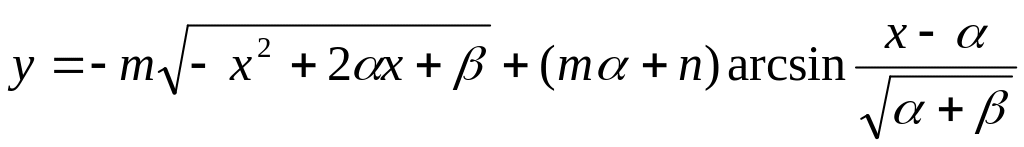
Нұсқа №5, 15




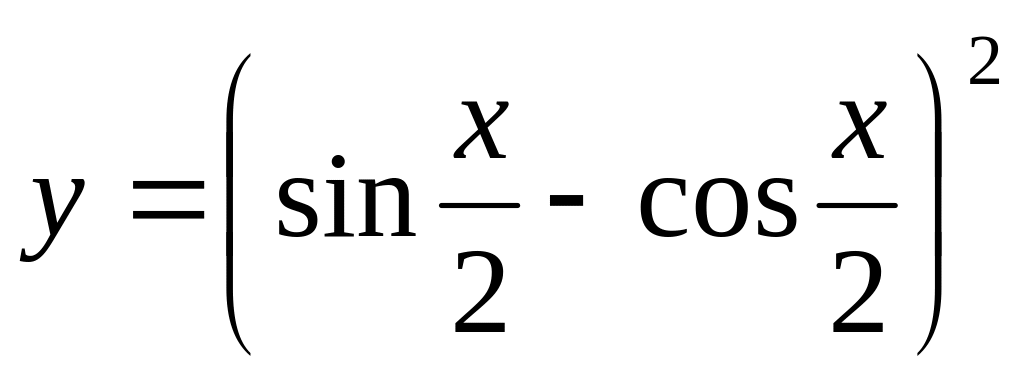

Есептеңіз :
Есептеңіз :
Есептеңіз :
Нұсқа №6, 16.


Есептеңіз :
Есептеңіз :

Нұсқа №7, 17.

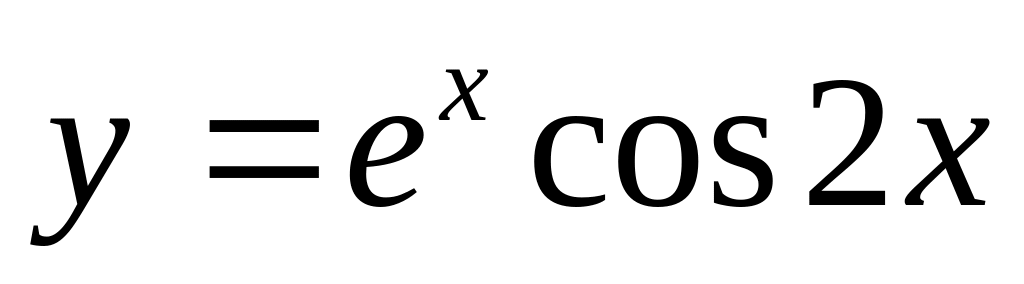
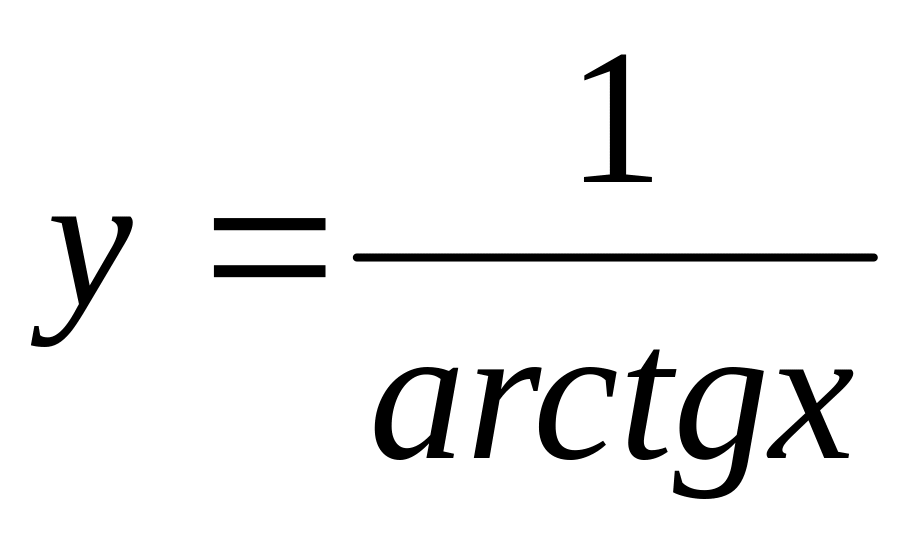
Есептеңіз :
Есептеңіз :


;
Нұсқа №8, 18.

Есептеңіз :
Есептеңіз :
;
Нұсқа №9, 19.
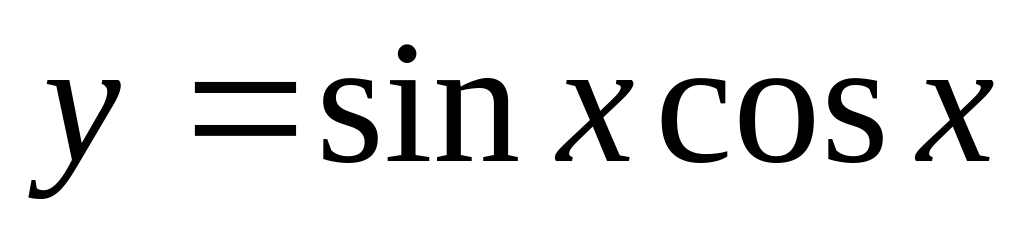

Есептеңіз
 :
: 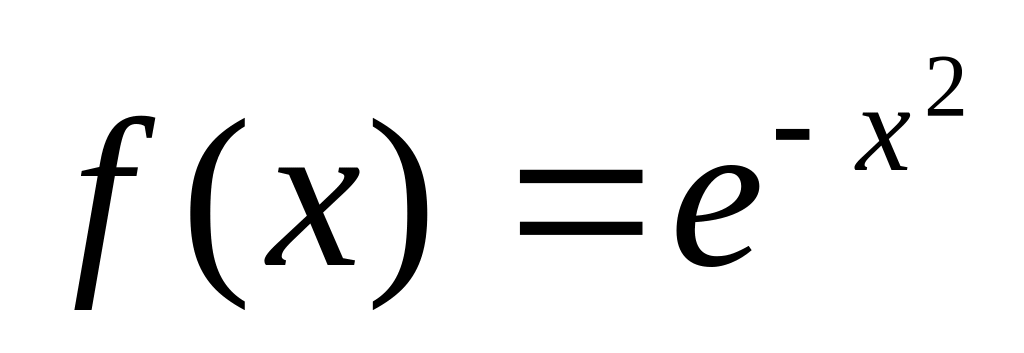
Есептеңіз :
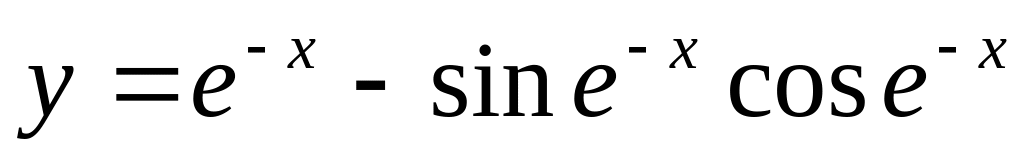
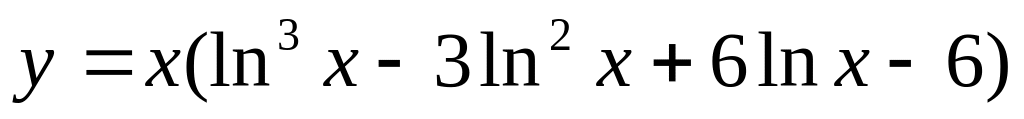
Нұсқа №10, 20.

Есептеңіз :

Есептеңіз :
Есептеңіз :
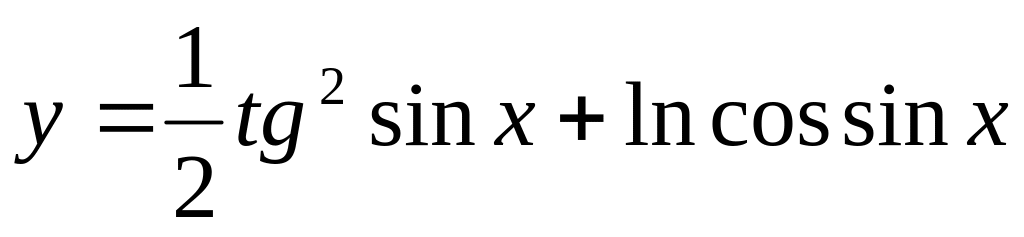
Жеке тапсырма №6 Тақырыбы: «бірнеше айнымалылы функция».
Мақсаты: Көп айнымалылы функциялардың толық зерттеуін еркін жүргізу, бірінші және екінші ретті дербес туындыларды, аралас туындыларды таба білу
Тапсырма:
Дербес туындылар және бірінші ретті толық дифференциал
Барлық дербес туындылар және екінші ретті толық дифференциал
Теңдеулер жүйесін шешу арқылы стационар нүктелерін:
![]() ,
,
![]()
Әрбір стационар нүктелері үшін дискриминант құрастырыңыз ∆=АС-В2, мұндағы А=
 ,
В=
,
В= ,
С=
,
С=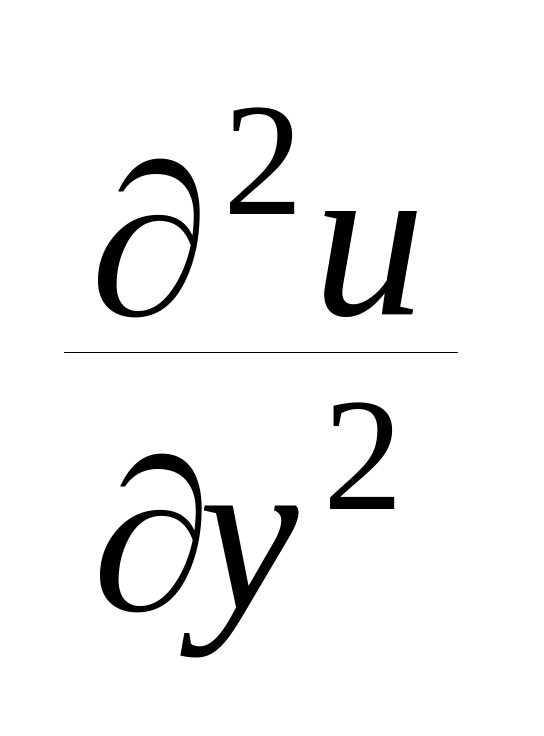
Егер бар болса, функцияның экстремумын және экстремум нүктесіндегі функцияның мәнін
М нүктесіндегі функцияның градиент шамасы және бағытын
u =х2-2х+1+2у2, М(1;1)
u=ех-у(х2-2ху +2у2), М(1;1)
u=х2+ху+ у2-2х-у, М(1;1)
u=6х3у2-х4у2- х3у3, М(1;1)
u=х4+ у4+4ху-2у2-2х2, М(1;1)
u=(х2+2у2)е-(х+у),М(1;1)
u=1-(х2+у2)2/3, М(1;1)
u=(х2+у2)е-(х+у), М(1;1)
u=(1+х-у)/√1+х2+у2, М(1;1)
u=8/х+х/у+у, М(1;1)
u=ех-у(х2-2у2), М(1;1)
u =х3+3ху2-15х-12у, М(1;1)
u=3х+6у-х2-ху-у2, М(1;1)
u=sinхsinу, М(П/4; П/4)
u= х3-2у3-3х+6у, М(0;0)
u=хуLn(х2+у2) , М(e/√2; e/√2)
u =ех+2у(х2-у2), М(-4/3;2/3)
u =1/2х2-4ху+9у2+3х-14у+1/2, М(2;1)
u =х2-ху+у2, М(1;1)
u =х3+у3-х2-2ху-у2, М(1;1)
u =(х-2у)е-(х+у), М(0;0)
u =х/у+1/х+у, М(2;1)
u =4х3+3х2у+3ху2-у3, М(1;1)
u =х2-2х-2у2-1, М(1;1)
u =х2+у2-2х-4√ху-2у+8,М(1;1)
u =2х3-ху2+5х2+у2, М(0;1)
u =3х2-2х√у+у-8х+8, М(1;4)
u =уLnх, М(e; e)
u =х2-ху-у2, М(1;1)
u =х3-2х2у2+у4, М(1;1)
u =sinх+sinу+sin(х+у), М(0;0)
u =ху+1/(2(х+у)), М(1;0)
u =х2-2ху+2у2+2х, М(1;1)
u =ху√1 -х2/ а2- у2/в2, М (1;0)
