§14. Характеристическое уравнение. Его инвариантность относительно замены базиса

Пусть — линейный оператор пространства V(P); —— базис V(P);

х — собственный вектор оператора принадлежащий собственному значению ;

— матрица оператора в базисе (1).

Запишем формулу связи между координатами образа и прообраза:

Это матричное уравнение запишем в виде системы:

или

Система (2) имеет ненулевое решение тогда и только тогда, когда определитель матрицы этой системы равен 0,

или

Определение

Матрица называется характеристической матрицей матрицы А.

Многочлен называется характеристическим многочленом, а уравнение называется характеристическим уравнением матрицы А или характеристическим уравнением оператора .

Равенство (3) показывает, что все собственные значения линейного оператора и только они являются корнями его характеристического многочлена.

Кратностью собственного значения линейного оператора называют кратность, с которой входит в качестве корня в характеристический многочлен оператора .

Вернемся к системе (2). Видим, что вектор тогда и только тогда есть собственный вектор оператора , принадлежащий собственному значению , когда координатная строка вектора х является ненулевым решением системы (2).

Задача. Найти собственные значения и соответствующие им собственные векторы линейного оператора пространства , если в некотором базисе оператор задан матрицей

Решение. Составим характеристическое уравнение оператора и найдем его корни. Действительные корни этого уравнения есть собственные значения оператора

. =

Собственными векторами, принадлежащими собственному значению будут те и только те ненулевые векторы, которые удовлетворяют условию то есть являются решениями системы (2) при

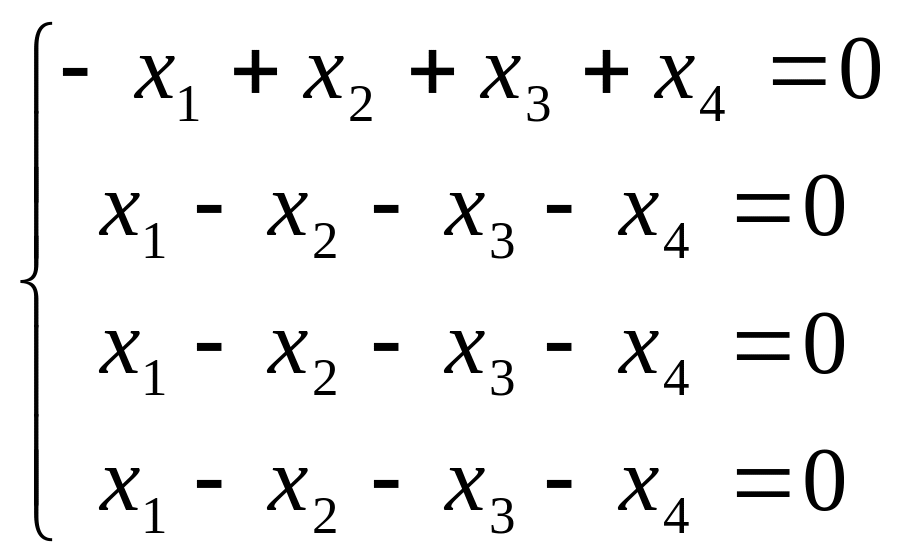Общее решение системы .

Составим фундаментальную систему решений:

х1	х2	х3	х4
( 1 ( 1 ( 1	1 0 0	0 1 0	0 ) = а1 0 ) = а2 1 ) = а3

Пространство решений этой системы

Множество собственных векторов, принадлежащих собственному значению есть \ . Собственными векторами для будут те и только те ненулевые векторы, которые удовлетворяют условию то есть являются решениями системы (2) при .

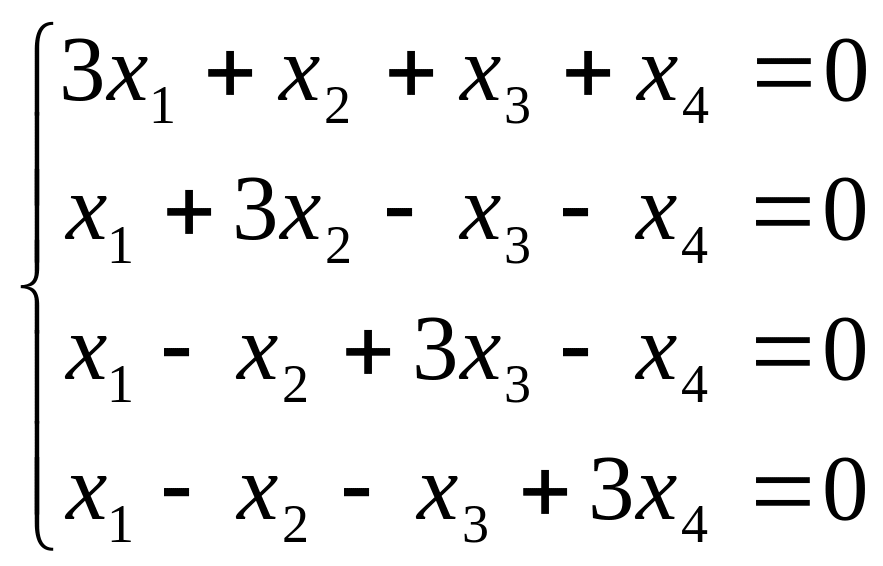Общее решение системы :

Составим фундаментальную систему решений:

х1	х2	х3	х4
( -1	1	1	1 ) = b

пространство решений системы L(b).

Множество собственных векторов, принадлежащих собственному значению есть L(b)\ .

Теорема 1

Подобные матрицы имеют равные характеристические многочлены.

Доказательство

Пусть матрицы А и В подобны. Это значит, что где . Покажем, что

что требовалось доказать.

Теорема 2

Характеристический многочлен линейного оператора инвариантен при изменении базиса.

Доказательство

Матрицы линейного оператора в различных базисах подобны.

По теореме 1 они имеют одинаковые характеристические многочлены.

Что требовалось доказать.