§ 5. Область значений и ранг линейного оператора

Пусть — векторное пространство, — линейный оператор пространства V; . Каждый вектор оператором отображается в — образ вектора а, который, вообще говоря, может и не принадлежать М. Совокупность образов всех векторов из М будем называть образом М и обозначать . Если , то .

Определение

Множество называется образом или областью значений линейного оператора пространства V.

Теорема 1

Область значений линейного оператора пространства V есть подпространство пространства V(P).

Доказательство

Для любых найдутся векторы , такие, что

так как то

тогда

таким образом - подпространство пространства V(P).

Определение

Рангом линейного оператора называется размерность его области значений

Теорема 2

Ранг линейного оператора ненулевого конечномерного пространства равен рангу матрицы этого оператора в какой-либо координатной системе.

Доказательство

Пусть — координатный базис V(P), — линейный оператор пространства V.

то есть

следовательно,

Размерность совпадает с рангом системы векторов Если А — матрица оператора в базисе то ее столбцы — координаты векторов значит

§ 6. Ядро и дефект линейного оператора

Определение

Ядром линейного оператора , действующего на пространстве V(P), называется множество всех векторов из V, которые оператором отображаются в ; обозначается ядро так:

Теорема 1

Ядро линейного оператора , действующего на пространстве V(P), является подпространством пространства V(P).

Доказательство

Проверим выполнимость для условий из теоремы о подпространстве.

следовательно, .

значит,

Таким образом, является подпространством пространства V(P).

Определение

Дефектом линейного оператора называется размерность его ядра.

Обозначение: .

Теорема 2

Пусть — линейный оператор конечномерного векторного пространства V(P).

Тогда сумма ранга и дефекта оператора равна размерности V(P).

Доказательство

Пусть где

—

— матрица оператора в некотором координатном базисе . Возьмем любой .

Пусть

Запишем формулу связи между координатами х и :

.

Это матричное уравнение запишем в виде системы

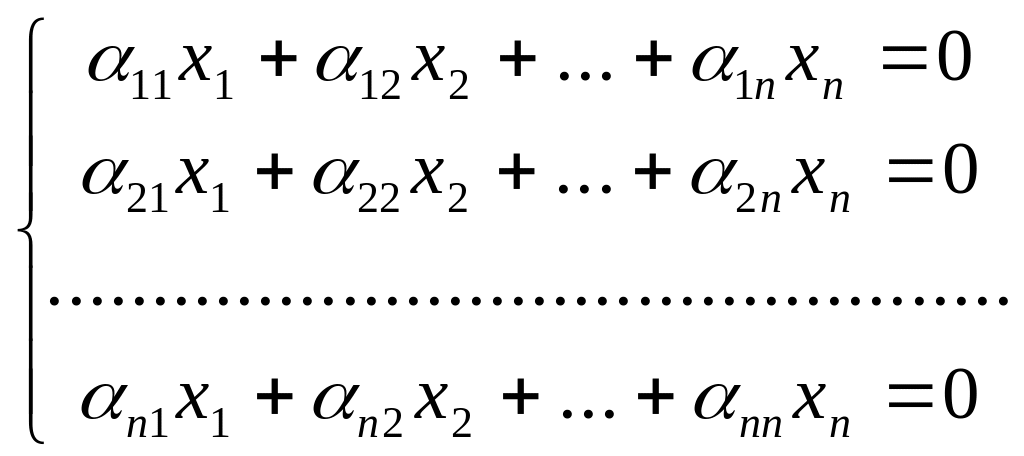(1)

Видим, что тогда и только тогда, когда его координаты удовлетворяют системе (1). Следовательно, совпадает с пространством решений системы (1), поэтому где Получаем, что

Задача. Линейный оператор пространства в базисе задан матрицей . Найти образ вектора . Найти ядро, дефект, область значений и ранг .

Решение

1. Найдем Запишем формулу связи между координатами векторов х и :

Таким образом,

2. Найдем . По определению ядра , если .

Пусть тогда

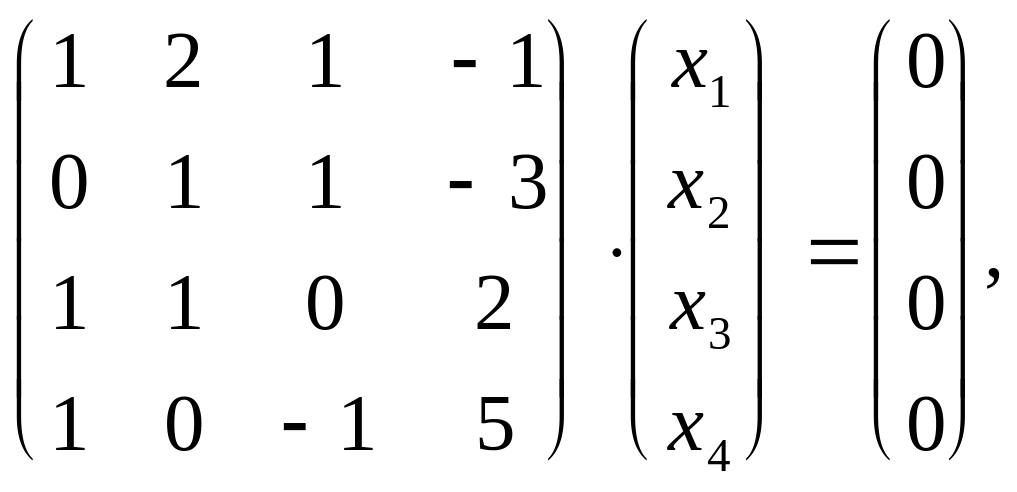или или

Ядро совпадает с пространством решений последней системы, решим ее.

.

.

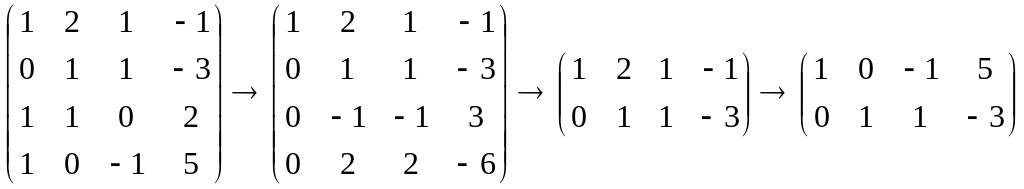Найдем фундаментальную систему решений.

х₁ х₂ х₃ х₄

_______________________

(1 -1 1 0) = а₁

(-5 3 0 1) = а₂

3. Найдем область значений оператора .

.

.

Координатные столбцы векторов — это столбцы матрицы А. Так как то в качестве базиса подпространства можно взять любые два непропорциональных столбца матрицы А, например, и

Таким образом,

или