Тема 6. Алгоритмы размещения элементов

6.1 Общая характеристика алгоритмов

Задача размещения элементов является одной из основных задач конструкторского проектирования электронных устройств и состоит в определении оптимального пространственного расположения элементов на коммутационном поле. В качестве критериев оптимальности размещения могут быть приняты различные характеристики схемы соединений элементов или конструкции узла в целом. Чаще выбирают один главный критерий – критерий минимума суммарной длины соединений (МСД). Могут быть наиболее важными критериями такие критерии как число пересечений соединений, число слоев коммутации и т.д.

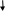
Алгоритмы размещения

Математические модели

Конструктивные алгоритмы начального размещения

Итерационные алгоритмы размещения

Непрерывно- дискретные методы

Метод ветвей и границ

Аналитические методы оптимизации

Последовательные алгоритмы

Параллельно- последовательные алгоритмы

Алгоритмы парных перестановок

Алгоритмы групповых перестановок

Методы случайного поиска

Методы силовых функций

Методы последовательного сдвига

Алгоритмы последовательного размещения по связности

Матричные алгоритмы размещения

Метод обратного размещения

Метод разбиения

Рис.6.1 Классификация алгоритмов размещения

Алгоритмы размещения делятся на четыре группы (рис.6.1):

1. Алгоритмы решения математических задач, являются моделями задачи размещения.

2. Конструктивные алгоритмы начального размещения.

3. Итерационные алгоритмы улучшения начального варианта размещения.

4. Непрерывно-дискретные методы размещения.

К первой группе относится метод ветвей и границ для задачи квадратичного назначения, к которой при определенных упрощениях сводится задача размещения: набор позиций считается фиксированным, элементы рассматриваются как геометрические точки, схема соединений представляется взвешенным графом соединений. Другой класс моделей связан с оптимизацией размещения на непрерывной плоскости, когда набор позиций для установки заранее не фиксирован.

Вторая и третья группы включают приближенные алгоритмы, предназначенные для оптимизации размещения элементов в фиксированном наборе позиций.

Четвертая группа алгоритмов предназначена для конструкций, в которых позиции для установки элементов заранее не фиксированы. Исходной базой для построения алгоритмов данной группы являются непрерывные модели и механистические аналоги задачи размещения.