Практична робота № 2 Визначення оптимальної частоти і глибини нагріву свч сталевої циліндрової деталі при поверхневому загартуванні з самовідпуском

Мета роботи: отримати початкові навички визначення оптимальних параметрів поверхневого високочастотного нагріву при термообробці деталей.

ТЕОРЕТИЧНІ відомості

Сталеву циліндрову деталь радіусом R, нагріту СВЧ на глибину δ до температури , потрібно загартувати на глибину Х_к (див. рис. 2.1 а) з такою умовою, аби після різкого однократного охолодження поверхневого шару товщиною до температури (загартування на мартенсит) частина тепла, що залишилася в шарі завтовшки Х_к, розподіляючись з однаковою швидкістю як назовні, так і всередину деталі на глибину Х_к, викликала розігрів (самовідпуск) загартованого шару до заданої температури самовідпуску

Рис. 2.1. Схеми розташування різних температурних зон при поверхневому загартуванні СВЧ з самовідпуском: а – схема розташування зон; б – схема розподілу температур в зонах (λ – напрями відведення тепла)

Визначити: на яку глибину δ слід нагрівати деталь, аби після різкого охолодження поверхневого шару на глибину Х_к відбувся його самовідпуск до температури .

При виконанні вправи прийняті наступні допущення:

– температура шару завтовшки δ рівна ;

– температурні кордони між шарами не плавні, а різкі як схематично показано на рис 2.1б;

– у момент перед початком самовідпускка температура загартованого шару Х_к і серцевини деталі однакова і рівна ;

– тепловіддачею в довкілля і витоком тепла уздовж осі виробу нехтуємо;

– вважаємо, що теплоємність шарів не залежить від температури.

З рис. 2.1 а, б витікає, що після різкого регламентованого охолодження поверхні деталі на глибину Х_к залишається гарячий шар завтовшки, рівному β, що має температуру загартованого нагріву ( ). Тепло з шару β починає приблизно з однаковою швидкістю поширюватися як в зовнішні шари, так і всередину деталі, при цьому шар β охолоджується, а суміжні шари нагріваються також приблизно однаково. Коли на поверхні деталі температура досягає максимального значення ( ), така ж температура буде і на відстані Х_к від шару β углиб до осі деталі, тобто у цей момент в шарі завтовшки 2Х_к + β температура буде однаковою. Це і буде максимальна температура самовідпуску ( ).

Таким чином, внутрішній гарячий циліндровий шар завтовшки β розігрів ще два суміжних з ним шаруючи товщиною Хк до температури , а сам охолодився до цієї ж температури.

Оскільки по умові завдання обміну теплом з довкіллям і внутрішніми шарами деталі не відбувається, та кількість тепла, що спочатку міститься в шарі β, не змінилося, а залишилося тим же і після досягнення температури самовідпуску в шарі завтовшки, рівному 2Х_к + β

Виходячи з рівняння теплового балансу, можна написати

Q_β = Q_{(2Хк + β)} (2.1)

де Q_β – кількість тепла, що міститься в гарячому циліндровому шарі завтовшки β при температурі ; Q_{(2Хк + β)} – кількість тепла, що міститься в шарі завтовшки 2Х_к + β при температурі самовідпуску .

У свою чергу, враховуючи, що ради спрощення початкова температура металу прийнята умовно рівною нулю, отримаємо

Q_β = m_β ·c_p· t⁰_к (2.2)

І

Q_{(2Хк + β)}= m_{(2Хк + β)}· c_p· t⁰_с (2.3)

де m_β і m_{(2Хк + β)} – маси циліндрових шарів завтовшки β і (2Хк + β), заввишки l, відповідно; с_p – питома теплоємність сталі; і – температури нагріву під загартування і розігрівання при самовідпуску, відповідно.

Виходячи з рівності Q_β і Q_{(2Хк + β)} для спрощення прийнявши К = , а =R/Х_К обчислити значення β:

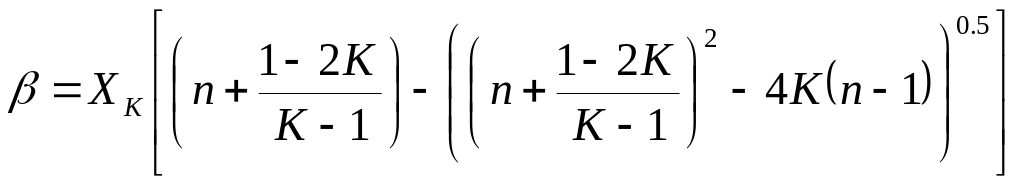(2.4)

Глибина нагріву δ_гор (див. рис. 2.1 а) визначиться як

δ_гор = Х_к + β (2.5)

Використовуючи формулу Гюйгенса для гарячої глибини проникнення СВЧ в гарячу сталь при глибинному способі нагріву, з рівняння

(2.6)

знайти значення оптимальної частоти СВЧ.