Уроки 3-4

Тема: Правила суми та добутку. Упорядкована множина. Перестановка. Розміщення. Комбінації.

Мета: Ознайомити учнів з двома основними законами комбінаторики; ввести поняття впорядкованої множини, перестановки, розміщення та комбінації; навчити розрізняти види сполук і знаходити їх число за відповідними формулами, використовуючи закони комбінаторики; розвивати пізнавальну діяльність учнів під час розв’язування вправ, формувати прийоми виділення головного.

Хід уроку

1. Перевірка домашнього завдання.

а) Запитання для усного опитування:

1. Предмети, з яких складається множина, називаються її…

2. Якими буквами позначаються множини?

3. Яким знаком позначають належності елемента даній множині?

4. Скінчена чи нескінчена множина простих чисел?

5. Яким символом позначають порожню множину?

6. Якщо множина B міститься у множині A, то множина B називається множини A.

7. Яким способом задається множина ?

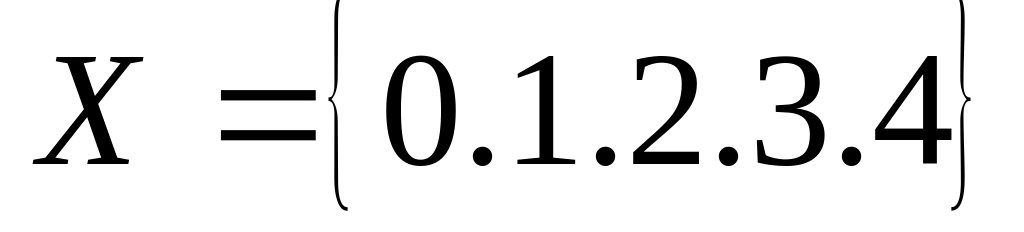8. Якщо множини A і B складаються з одних і тих самих елементів, то вони…

9. Чи є множина голубів підмножиною множини птахів? Зобразіть це діаграмою Ейлера.

10. Дано множину . Запишіть усі її двохелементні підмножини. Скільки їх?

б) Перевірка розв’язування домашньої задачі № 2

, , , , , , ; .

в) Перевірка розв’язання домашньої задачі № 7

; .

г) Перевірка розв’язання домашньої задачі №11

Досить зручно розбити множину всіх студентів на підмножини, які не перетинаються, а саме:

-- студенти, які знають лише англійську мову;

-- студенти, які знають лише німецьку мову;

-- студенти, які знають лише французьку мову;

-- студенти, які знають англійську і німецьку мови;

-- студенти, які знають англійську і французьку мови;

-- студенти, які знають німецьку і французьку мови;

-- студенти, які знають англійську, німецьку французьку мови;

-- студенти, які не знають ні англійської, ні німецької, ні французької мови.

Тоді за умовою задачі

; ; тому ;

; звідси ;

; тому ;

; ; звідси ;

;

тому ;

.

Отже, англійську мов вивчають (це множини ) всього 10+0+5+3=18 студентів; англійську і німецьку мови, але не французьку не вивчає (це множина ) жоден студент; французьку, але не англійську мову вивчають (це множини ) всього 35+5=40 студентів.

Задача 1. скільки чисел серед перших 100 натуральних не ділиться ані на 2; ані на 3; ані на 5 ?

Розв’язання:

Нехай М – множина чисел, які діляться хоча б на одне з цих чисел,

А – множина чисел, які діляться на 2,

В – множина чисел, які діляться на 3,

С – множина чисел, які діляться на 5.

Тоді -- множина чисел, які діляться на 2 і 3 одночасно, тобто на 6;

-- множина чисел, які діляться на 2 і 5 одночасно, тобто на 10;

-- множина чисел, які діляться на 3 і 5 одночасно, тобто на 15;

-- множина чисел, які діляться на 2,3 і 5 одночасно, тобто на 30.

Тоді

Шукана множина містить 10-74=26 чисел.

2. Пояснення нового матеріалу.

Дуже часто при розв’язуванні задач доводиться давати відповіді на такі запитання:

• Скільки існує елементів з заданими властивостями? (Визначити кількість діагоналей в многокутнику, граней в піраміді, найбільшу кількість прямокутних граней у похилому паралелепіпеді і т.д.)

• Чи існує хоча б один елемент з заданими властивостями? (трикутник з периметром10 см. чи сумою кутів 200 градусів)

• Скільки розв’язків має задача? (підрахунок способів вибору редколегії стінгазети)

Усі ці задачі є комбінаторами. Вони розглядають скінченні множини елементів довільної природи або сполуки, які носять певну назву: перестановки, розміщення і комбінації. Вивчення цих сполук та двох основних правил розв’язування комбінаторних задач і є темою сьогоднішнього уроку.

Насамперед, введемо поняття впорядкованої множини. Це множина для якої порядок розміщення елементів має істотне значення, тобто n елементи є пронумеровані.

Наприклад, з елементів а, в, с можна утворити такі впорядковані множини

Два правила розв’язування комбінаторних задач:

А) Правило суми: Якщо елемент а можна вибрати m способами, а елемент b – n способами, то вибір a або b можна здійснити m + n способами.

Б) Правило добутку: Якщо елемент a можна вибрати m способами та якщо після кожного такого вибору елемент b можна вибрити n способами, то вибір пари a і b можна здійснити m*n способами.

Ці правила можна проілюструвати на такому простому прикладі: якщо на столі лежать 5 різних олівців та 4 ручки, то вибрати якийсь один з предметів (ручку або олівець) ми можемо 5+4=9 способами, а вибрати один олівець і одну ручку 5*4=20 способами. бо вибір олівця і вибір ручки не пов’язані між собою, тобто незалежні. надалі ви помітите, що інтуїтивно ці правила ми використовуємо увесь час при розв’язуванні логічних задач комбінаторного характеру (на сукупності предметів).

В) Перестановки

Означення. Будь-яка впорядкована множина, яка складається з заданих n-елементів, називається перестановкою із n-елементів.

Число перестановок із n-елементів позначають через . Р – перша буква французького слова «permutation» -- «перестановки».

Будемо для стислості добуток , тобто добуток всіх натуральних чиселn до одиниці, позначати символом n! (читається «ен факторіал»)

Задача 1 Скільки шестизначних чисел, кратних п’яти, можна скласти із цифр 1,2,3,4,5,6 за умови, що в числі цифри не повторюються?

Розв’язання: так як на місці одиниць повинна знаходитись цифра 5, то для 1-ої цифри є 5 варіантів, для 2-ої 4, 3-ьої 3 і т.д. в порядку зменшення. Шукана кількість становитиме

У загальному випадку число перестановок з n- елементів , бо для вибору першого елемента є n можливостей, а з кожним наступним їх кількість зменшується на одинцю.

таким чином, в множині, що містить n- елементів, встановити певний порядок послідовності елементів або, як кажуть, упорядкувати таку множину можна n! способами.

Наприклад, список учнів класу, в якому 20 чоловік і немає однофамільців, можна скласти способами.

Вправа 16 (ст. 445) Скільки треба взяти елементів, щоб число перестановок, утворюваних х них дорівнювало 5040?

Розв’язання:

Щоб знайти це число, необхідно передбачити факторіали натуральних чисел. Маємо

Спів падання результату дає розв’язок 7.

Відповідь: 7 елементів.

Для факторіала є така чудова залежність , яка часто використовується.

Вправа 13 (ст. 444)

Обчислити: а) б)

Розв’язання:

а)

б)

Г) Розміщення

До подання розміщення приводить розв’язання такої задачі:

Задача 2. В сьомому класі вивчається 14 предметів. Скількома способами можна скласти розклад занять на суботу, якщо у цей день тижня має бути 5 різних уроків?

Розв’язання:

На перший урок можна розмістити один із 14 предметів, на другий один з решти 13 предметів; на третій – один з 12, які лишились і т. д., тобто шукана кількість способів – це кількість впорядкованих п’яти елементних підмножин даної множини і їх кількість становить .

Означення. Нехай є множина , яка містить n- елементів. Кожна її опорядкована підмножина, що складається з k- елементів ( ), називається розміщенням з n елементів по k елементів.

Виведемо формулу підрахунку числа усіх розміщень із n –елементів по k –елементів. Для позначення цього числа застосовується спеціальний символ (читається: «число розміщень із n по k » або « А із n по k». А – перша буква французького слова «arrangement», що означає «розміщення, приведення у порядок».

У загальному випадку на питання про число розміщень із n –елементів по k –елементів дає відповідь така формула:

(1)

тобто число розміщень із n –елементів по k –елементів дорівнює добутку k послідовних натуральних чисел від n до включно.

Формулу (1) зручно записувати в іншому вигляді, використовуючи позначення факторіала. Для її виведення помножимо і поділимо добуток, що стоїть в правій частині формули (1) на Тоді отримаємо формулу:

(2)

Задача 3 Відомо, що вибрати старосту класу і його заступника можна 600 способами. Скільки учнів навчається в цьому класі?

Розв’язання:

Нехай у цьому класі n учнів. Тоді, за умовою. , тобто , звідси . Єдиний корінь цього рівняння, що задовольняє умову, . Отже, в класі 25 учнів.

Д) Комбінації

Дуже часто підмножини не потрібно впорядковувати, тобто для них є неістотним порядком вибору елементів, а враховується лише результат.

Задача 4. Скільки екзаменаційних комісій, що складаються із 7 членів, можна утворити із 14 викладачів?

Очевидно, порядок вибору значення не має і комісій буде стільки, скільки існує семи елементних підмножин у чотирнадцятиелементної множини.

Означення. Нехай є множина, що складається із n –елементів. Кожна її підмножина (не впорядкована), що містить k –елементів, називається комбінацією із n –елементів по k –елементів.

Число всіх комбінацій з n –елементів по k –елементів позначається символом (читається: «число комбінацій із n по k» або «це із n по k»)

С – перша буква французького слова «combinasion» «комбінація».

Строге виведення формули формули кількості комбінацій спирається на використання методу математичної індукції. Більш спрощене випливає із такого співвідношення: , яке ілюструє той факт, що кількість впорядкованих k-елементних підмножин дорівнює добутку кількості невпорядкованих k-елементних підмножин, помножених на кількість перестановок, тобто способів їх впорядкування.

З цієї залежності отримуємо формулу

У загальному випадку число комбінацій із n-елементів визначається такою формулою:

(3)

Формулу (3) можна записати в іншому, більш зручному для обчислень вигляді, а саме, число комбінацій із n-елементів по k-елементів дорівнює добутку всіх натуральних чисел від n до включно, діленому на k!

(4)

Очевидно, розв’язок задачі 4 матиме вигляд

Вправа 18 (ст. 445) Скільки різних прямих можна провести через 15 точок площини, з яких ніякі три не лежать на одній прямі?

Розв’язання:

Так як ніякі три точки не лежать на одній прямій, то будь-яка пара точок задає пряму. Так як порядок вибору точок не має ніякого значення, то шукана кількість є комбінацією з 10 елементів по 2, а це становить .

Е) Властивості комбінацій:

1.

2.

3.

4.