Формализация[править | править исходный текст]
Шаг 1. Задаются начальные границы отрезка
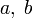и
точность 
.Шаг 2. Рассчитывают начальные точки деления:
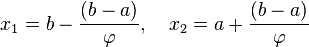и
значения в них целевой
функции: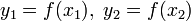 
.Если
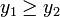(для
поиска max изменить неравенство на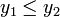 
),
то 
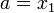
Иначе
.
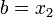Шаг 3.
Если
,
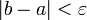то 
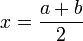и
останов.Иначе возврат к шагу 2.
Алгоритм взят из источника: Джон Г.Мэтьюз, Куртис Д.Финк "Численные методы. Использование MATLAB". — М, СПб: "Вильямс", 2001. — 716 с.
Метод чисел Фибоначчи[править | править исходный текст]
В
силу того, что в асимптотике 
,
метод золотого сечения может быть
трансформирован в так называемый
метод чисел
Фибоначчи.
Однако при этом в силу свойств чисел
Фибоначчи количество итераций строго
ограничено. Это удобно, если сразу задано
количество возможных обращений к
функции.
Алгоритм[править | править исходный текст]
Шаг 1. Задаются начальные границы отрезка и число итераций
,
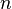рассчитывают начальные точки деления: 
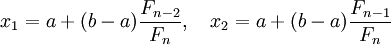и
значения в них целевой
функции:
.Шаг 2.
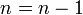.Если
,
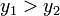то 
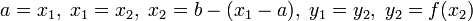.Иначе
.
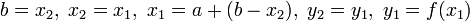Шаг 3.
Если
,
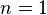то 
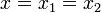и
останов.Иначе возврат к шагу 2.
Карт-чек N45377063
25.03.2014 14:35:37
Банковская карточка 676821******1506
Отправитель платежа: "ОАО "Белгазпромбанк" код 742
Плательщик: Нестеренко Любовь Леонидовна, г. БОРИСОВ,
ул. ФАБРИЧНАЯ, д.19,
Получатель платежа: "Минский институт управления", УНП
100687805, р/с 3015012260011 в "Открытое акционерное
общество "БПС-Сбербанк" код 369
Назначение платежа: экзамен
Оплачено по услуге: 90 000 BYR
Комиссия : 900 BYR
Сумма : 90 900 BYR
Код авторизации: 386509
RRN: 000004687898