
- •Нахождение корней линейной системы методом Зейделя
- •Метод золотого сечения
- •Описание метода
- •Анализ метода
- •Рекомендации в выборе параметров
- •Метод золотого сечения
- •Описание метода[править | править исходный текст]
- •Алгоритм[править | править исходный текст]
- •Формализация[править | править исходный текст]
- •Метод чисел Фибоначчи[править | править исходный текст]
- •Алгоритм[править | править исходный текст]
Сходство метода Зейделя и метода простых итераций в том, что это по сути один и тот же метод, но при простых итерациях вектор X' = (x'1,x'2,...,x'n) получается из вектора X = (x1,x2,...,xn), т.е. X' = (k11x1+k12x2+...+k1nxn, k21x1+k22x2+...+k2nxn, ..., km1x1+km2x2+...+kmnxn), у Зейделя вектор X' получается так: X' = (k11x1+k12x2+...+k1nxn, k21x'1+k22x2+...+k2nxn, ..., km1x'1+km2x'2+...+kmnxn) т.е. при рассчёте второго компонента X' (x'2) используется уже рассчитанный компонент x'1 - вот и всё различие.
Метод итерации
Пусть дана линейная система (13). Введя в рассмотрение матрицы (15), систему (13) коротко можно записать в виде матричного уравнения (14). Предполагая, что диагональные коэффициенты aij не равны 0 (i = 1, 2, …, n),
разрешим первое уравнение системы (13) относительно х1, второе - относительно х2 и т. д. Тогда получим эквивалентную систему
|
(18) |
где
![]() при i не
равно j
при i не
равно j
и ij = 0 при i = j (i, j = 1, 2, …, n).
Введя матрицы
 и
и 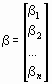 ,
,
систему (18) можно записать в матричной форме
x = + x,
а любое (k + 1) приближение вычисляется по формуле
x (k+1) = + x (k). |
(19) |
Напишем формулы приближений в развернутом виде:
|
(19' ) |
Приведем достаточное условие сходимости метода итераций.
Теорема: Процесс итерации для приведенной линейной системы (18) сходится к единственному ее решению, если какая-нибудь каноническая норма матрицы меньше единицы, т.е. для итерационного процесса (19) достаточное условие есть
|
(20) |
Следствие 1. Процесс итерации для системы (18) сходится, если:
1) ![]() <
1 (m-норма
или неопределенная норма)
<
1 (m-норма
или неопределенная норма)
или
2) ![]() <
1 (l-норма
или норма L1)
<
1 (l-норма
или норма L1)
или
3) ![]() <
1 (k-норма
или Евклидова норма).
<
1 (k-норма
или Евклидова норма).
Следствие 2. Для системы (13) процесс итерации сходится, если выполнены неравенства:
|
или , |
|
где штрих у знака суммы означает, что при суммировании пропускаются значения i = j, т. е. сходимость имеет место, если модули диагональных элементов матрицы А системы (13) или для каждой строки превышают сумму модулей недиагональных элементов этой строки, или же для каждого столбца превышают сумму модулей недиагональных элементов этого столбца.
Пример 6. Пусть
 .
.
Имеем:
![]() max(1+
2 + 3, 4 + 5 + 6, 7 + 8 + 9) = max (6, 15, 24) = 24;
max(1+
2 + 3, 4 + 5 + 6, 7 + 8 + 9) = max (6, 15, 24) = 24;
![]() max(1+
4 + 7, 2 + 5 + 8, 3 + 6 + 9) = max (12, 15, 18) = 18;
max(1+
4 + 7, 2 + 5 + 8, 3 + 6 + 9) = max (12, 15, 18) = 18;
![]() .
.
В Mathcad существуют специальные функции для вычисления норм матриц:
normi(A)
Возвращает неопределенную норму матрицы А.
norm1(A)
Возвращает L1, норму матрицы А.
normе(A)
Возвращает Евклидову норму матрицы А.
В качестве условия окончания итерационного процесса можно взять условие
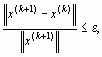
- заданная погрешность приближенного решения х x(k +1).
Пример 7. Решить систему
|
(21) |
методом итераций.
Диагональные коэффициенты 100; 200; 100 системы (21) значительно преобладают над остальными коэффициентами при неизвестных, т.е., выполняется следствие 2.
Приведем эту систему к нормальному виду (18)
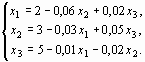
В матричной форме ее можно записать так:
 .
.

Рисунок 10.
На Рисунке 10 приведен фрагмент рабочего документа Mathcad, содержащий дальнейшее решение этой системы.
Метод Зейделя
Метод Зейделя представляет собой некоторую модификацию метода итераций. Основная его идея заключается в том, что при вычислении (k + 1)-го приближения неизвестной xi учитываются уже вычисленные ранее (k + 1)-е приближения неизвестных x1, x2, …,xi - 1.
Пусть
получена эквивалентная система (18).
Выберем произвольно начальные приближения
корней ![]() .
Далее, предполагая, что k-ые
приближения
.
Далее, предполагая, что k-ые
приближения ![]() корней
известны, согласно Зейделю будем строить
(k +
1)-е приближения корней по формулам:
корней
известны, согласно Зейделю будем строить
(k +
1)-е приближения корней по формулам:
|
(22) |
Заметим, что указанные выше условия сходимости для простой итерации остается верной для итерации по методу Зейделя. Обычно метод Зейделя дает лучшую сходимость, чем метод простой итерации, но приводит к более громоздким вычислениям.
Пример 8. Методом Зейделя решить систему уравнений

Приведем эту систему к виду, удобному для итерации:

В
качестве нулевых приближений корней
возьмем: ![]()
Применяя процесс Зейделя, последовательно получим:


Результаты вычислений с точностью до четырех знаков приведены в Таблице 2.
Таблица 2
Нахождение корней линейной системы методом Зейделя
i |
|
|
|
0 |
1,2000 |
0,0000 |
0,000 |
1 |
1,2000 |
1,0600 |
0,9480 |
2 |
0,9992 |
1,0054 |
0,9991 |
3 |
0,9996 |
1,0001 |
1,0001 |
4 |
1,000 |
1,000 |
1,000 |
5 |
1,000 |
1,000 |
1,000 |
Точные значения корней: х1 = 1; х2 = 1; х3 = 1.
Метод половинного деления
Для
нахождения корня уравнения (1),
принадлежащего отрезку [a, b],
делим этот отрезок пополам. Если f![]() =
0 , то =
=
0 , то = ![]() является
корнем уравнения. Если f
не
равно 0 (что, практически, наиболее
вероятно), то выбираем ту из половин
является
корнем уравнения. Если f
не
равно 0 (что, практически, наиболее
вероятно), то выбираем ту из половин ![]() или
или![]() ,
на концах которой функция f(x) имеет
противоположные знаки. Новый суженный
отрезок а1, b1 снова
делим пополам и производим те же самые
действия.
,
на концах которой функция f(x) имеет
противоположные знаки. Новый суженный
отрезок а1, b1 снова
делим пополам и производим те же самые
действия.
Метод половинного деления практически удобно применять для грубого нахождения корня данного уравнения, метод прост и надежен, всегда сходится.
Пример 3. Методом половинного деления уточнить корень уравнения
f(x) = x4 + 2 x3 - x - 1 = 0
лежащий на отрезке 0, 1 .
Последовательно имеем:
f(0) = - 1; f(1) = 1; f(0,5) = 0,06 + 0,25 - 0,5 - 1 = - 1,19;
f(0,75) = 0,32 + 0,84 - 0,75 - 1 = - 0,59;
f(0,875) = 0,59 + 1,34 - 0,88 - 1 = + 0,05;
f(0,8125) = 0,436 + 1,072 - 0,812 - 1 = - 0,304;
f(0,8438) = 0,507 + 1,202 - 0,844 - 1 = - 0,135;
f(0,8594) = 0,546 + 1,270 - 0,859 - 1 = - 0,043 и т. д.
Можно принять
= ![]() (0,859
+ 0,875) = 0,867
(0,859
+ 0,875) = 0,867
Постановка задачи
В данной статье рассмотрены симметричные методы поиска экстремума функции одного переменного.
Пусть
дана функция ![]() ,
необходимо найти минимум этой функции
на заданном отрезке
,
необходимо найти минимум этой функции
на заданном отрезке ![]() (задача
максимума решается аналогично).
Предполагается, что производная функции
либо не существует, либо сложно вычислима,
что не позволяет свести задачу к поиску
корней производной
(задача
максимума решается аналогично).
Предполагается, что производная функции
либо не существует, либо сложно вычислима,
что не позволяет свести задачу к поиску
корней производной ![]() .
.
Методы
заключаются в построении последовательности
отрезков ![]() ,
стаягивающихся к точке
,
стаягивающихся к точке ![]() .
.
Проанализируем симметричные методы поиска и оценим их эффективность и точность.
Требования к функции
Рассматривая
все функции, пусть даже непрерывные,
можно построить такой пример, что ![]() ,
хотя
,
хотя ![]() .
.
Гарантировать применимость рассматриваемых методов можно только для унимодальных функций.
Определение : Функция ![]() называется унимодальной на
отрезке
,
если ∃!
точка минимума
называется унимодальной на
отрезке
,
если ∃!
точка минимума ![]() на
этом отрезке такая, что для любых
точек
на
этом отрезке такая, что для любых
точек ![]() этого
отрезка
этого
отрезка
![]() ,
,
![]()
.
Другими словами унимодальная функция монотонна на обе стороны от точки минимума . Аналогично определяется унимодальная функция и для задачи на максимум. Унимодальные функции могут быть непрерывными, разрывными, дискретными...
Далее будем рассматривать только унимодальные функции. При этом предполагаем, что они определены в достаточном количестве точек.
Симметричные методы
В
классе симметричных
методов на
каждом шаге выбирается две точки
отрезка ![]() и
и ![]() ,
симметрично расположенных относительно
центра этого отрезка. Дальнейшие действия
определяются свойством унимодальной
функции:
Пусть функция
унимодальна
на отрезке
,
а ее минимум достигается в точке
.
Для любых точек
и
этого
отрезка и таких, что
,
симметрично расположенных относительно
центра этого отрезка. Дальнейшие действия
определяются свойством унимодальной
функции:
Пусть функция
унимодальна
на отрезке
,
а ее минимум достигается в точке
.
Для любых точек
и
этого
отрезка и таких, что ![]() верно
следующее:
верно
следующее:
если
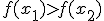 ,
то точка минимума
,
то точка минимума 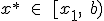 ,
,если
 ,
то точка минимума
,
то точка минимума 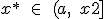 .
.
Исходя
из определения методов, видно, что всякий
симметричный метод полностью определяется
заданием отрезка
и
правилом выбора первой точки. Тогда
другая точка
находится
по правилу общему для всех симметричных
методов: ![]() .
.
Соответственно, методы различаются способом выбора симметричных точек и .




