1.2 Вычисление координат вершин замкнутого теодолитного хода
Уравнивание измеренных углов
Измерения горизонтальных углов сопровождаются неизбежными ошибками (невязками).
Угловая невязка вычисляется по формуле:
Если полученная невязка не превышает допустимую, то ее разбрасывают с обратным знаком на все измеренные углы, не дробя при этом менее чем на 0,1'
Вписывают полученные поправки (δβ) над значениями углов (графа 2 таблицы 2).
С учетом поправок и их знака вычисляют исправленные углы:
Контролем правильного уравнивания измеренных горизонтальных углов служит равенство суммы исправленных горизонтальных углов теоретической сумме.
Пример: для построения плана был проложен замкнутый теодолитный ход в виде пятиугольника (рис. 1), в котором были измерены правые по ходу горизонтальные углы.
Результаты измерений приведены в табл. 1.
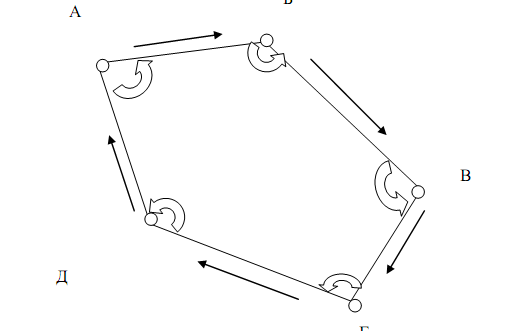
Рис. 1. Замкнутый теодолитный ход
Точки А, Б, В, Г, Д – станции замкнутого теодолитного хода и вершины горизонтальных правых по ходу углов. Стрелками показано направление хода.
Таблица 1.
Результаты измерения и исправления горизонтальных углов
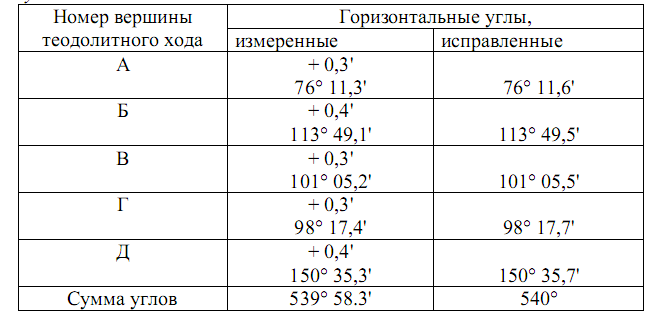
Теоретическую сумму внутренних углов пятиугольника (которым является наш замкнутый теодолитный ход) вычисляем согласно формулы 2:
180°(5 – 2) = 540°.
Определяем угловую невязку: 539° 58.3' - 540° = - 1,7'.
Вычисляем допустимую невязку:
Т. к. полученная невязка меньше допустимой по абсолютной величине, распределяем ее на все измеренные углы с обратным знаком, т. е. с плюсом; причем к большим углам прибавим большие поправки.
Проверяем сумму исправленных углов, она равна 540°.
Вычисление дирекционных углов сторон теодолитного хода
Дирекционный угол (α ) – это угол, отсчитываемый от северного направления осевого меридиана до рассматриваемой стороны по ходу часовой стрелки. Он изменяется от 0˚ до 360˚.
Вычисление дирекционных углов сторон теодолитного хода выполняют по формуле:
где α n-1 – дирекционный угол предыдущей стороны,
α n - дирекционный угол последующей стороны,
β прав.испр. – правый исправленный угол между рассматриваемыми сторонами.
Вычисление дирекционных углов ведется в столбик, при этом следует помнить, что в одном градусе – 60 минут.
Контролем верного вычисления дирекционных углов служит равенство заданного дирекционного угла и вычисленного начальной стороны теодолитного хода.
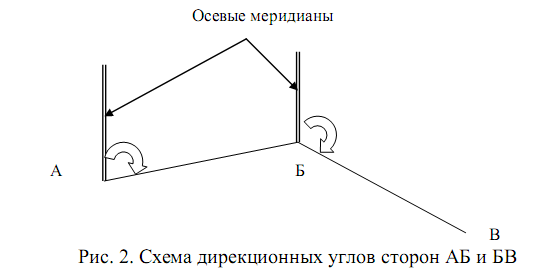
Пример: дирекционный угол стороны А-Б равен: 79° 58'.
Дирекционный угол стороны Б-В: 79° 58' + 180° - 113° 49,5' = 146° 08,5'
Дирекционный угол стороны В-Г: 146° 08,5' + 180° - 101° 05,5' = 225° 03'
Дирекционный угол стороны Г-Д: 225° 03' + 180° - 98° 17,7' = 306° 45,3'
Дирекционный угол стороны Д-А: 306° 45,3' + 180° - 150° 35,7' = 336° 9,6'
Дирекционный угол стороны А-Б: 336° 09,6' + 180° - 76° 11,6' = 439° 58'.
Если значения вычисленных дирекционных углов больше 360°,
перед занесением результатов в таблицу, вычитаем 360°.
Например: дирекционный угол стороны А-Б: 439° 58'- 360° = 79° 58'.
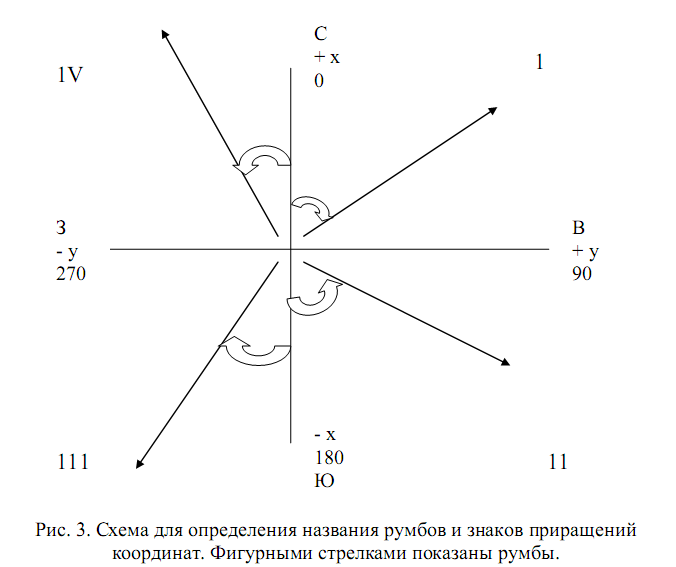
Определение румбов и знаков приращений координат
Румб – это острый угол, отсчитываемый от ближайшего окончания осевого меридиана до ориентируемой линии.
Вычисление румбов осуществляется в зависимости от того, в какой четверти геодезических прямоугольных координат находится ориентируемая линия.
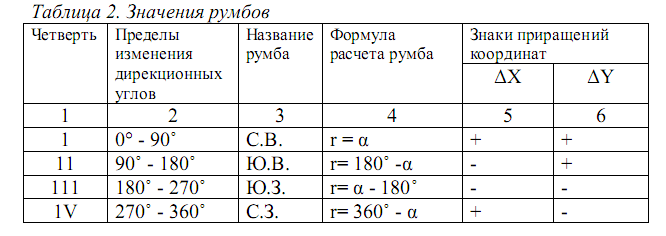
Знаки приращений координат определяются также по положению рассматриваемой стороны, т.е. в зависимости от того, в какой четверти геодезических прямоугольных координат находится конкретная сторона теодолитного хода.
Пользуясь таблицей 2 или рисунком 3, определить значения румбов, их название относительно сторон света, знаки приращений координат; результаты занести в соответствующие графы таблицы 1 Приложения 2.
Например:
Дирекционный угол стороны Б-В: 146° 08,5', следовательно она находится во второй четверти.
Название румба Ю.В.
Значение 180˚ - 146° 08,5' = 33° 51,5'.
Знаки приращений координат:
для ΔX «минус»
для ΔY «плюс».
Вычисление приращений координат
Приращения координат вычисляют по формулам:
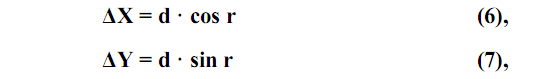
где: d – горизонтальное проложение стороны теодолитного хода,
r – значение румба соответствующей стороны хода.
Для вычисления приращений координат рекомендуется использовать микрокалькулятор с тригонометрическими функциями или «Четырехзначные математические таблицы Брадиса».
Пример вычисления приращения координат с использованием калькулятора:
горизонтальное проложение стороны хода равно 115,30 м, значение румба 58°36,3´.
ΔX = 115,30 м×cos 58°36,3´
До начала вычислений необходимо перевести значение угла из шестидесятичной системы исчисления в десятичную, для этого минуты угла делим на 60, результат суммируем с градусами.
ΔX =( 36,3/60 + 58) cos×115,30 м = 60,06 м
Аналогично вычисляем приращения по Y.
Результаты округляем до сотых и записываем в графы 9 и 11 таблицы 1 Приложения 2.
Уравнивание приращений координат
Уравнивание приращений координат заключается в нахождении ошибок, их распределения и исправления вычисленных значений приращений координат.
Линейные невязки вычисляются по формулам:
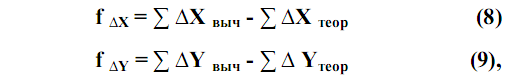
где: ∑ ∆X выч, ∑ ∆Yвыч – суммы приращений координат, вычисленные с учетом знаков;
∑ ∆Xтеор, ∑ ∆ Yтеор – теоретические суммы приращений координат.
Для замкнутого теодолитного хода, значения теоретической суммы приращений координат равны нулю, следовательно, невязки приращений координат будут равны их сумме вычисленных приращений, по величине они должны быть близки к нулю.
Чтобы проверить условие допустимости невязок, определяем:
1. абсолютное значение
2. относительное значение
где Р – периметр теодолитного хода ( сумма горизонтальных проложений).
Допустимая невязка равна 1/ 2000.
Если выполняется условие допустимости: | f отн | ≤ | f доп |, то невязки распределяют с обратным знаком, предварительно рассчитав поправки для приращений координат каждой стороны теодолитного хода по формулам:
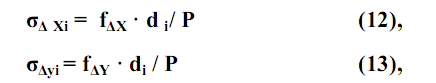
в которых индекс «i» обозначает номер стороны хода,
Р – периметр замкнутого теодолитного хода.
Поправки надписывают над соответствующими значениями приращений координат с обратным знаком, после чего производят вычисление исправленных значений приращений, учитывая при этом знаки поправок и знаки приращений.
Контролем верно проведенного уравнивания служит равенство сумм исправленных приращений координат нулю. Для упрощения вычисления поправок делят сумму приращений отдельно по « x» и по «y» на величину периметра (так как эти величины постоянны) и умножают последовательно полученные значения на горизонтальные проложения.
Пример уравнивания приращений координат приведен в таблице 3.
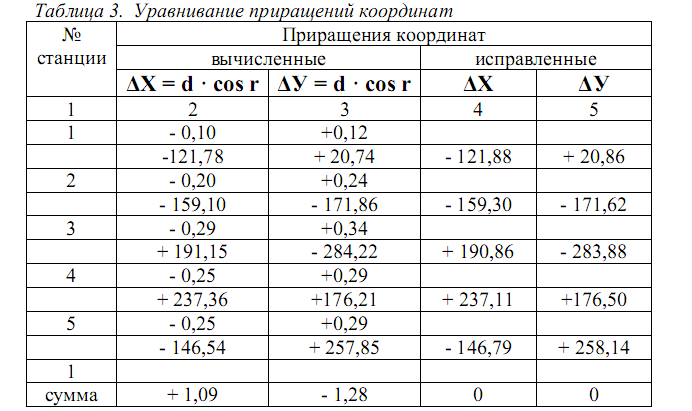
Вычисление координат вершин замкнутого теодолитного хода
Координаты всех вершин теодолитного хода вычисляют последовательно, начиная с вершины с известными координатами.
Координата последующей точки равна сумме координаты предыдущей точки и соответствующего исправленного приращения.
Контролем правильного вычисления координат замкнутого теодолитного хода служит получение расчетным путем координат начальной точки.
Графическая часть задания.
Построение плана теодолитной съемки
План теодолитной съемки строится в масштабе 1:2000.
Начинают построение плана с нанесения координатной сетки, состоящей из квадратов со сторонами 10 см.
Количество квадратов по осям (Nx; Ny) определяют по формулам:
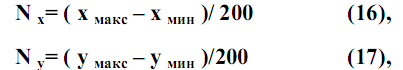
где xмакс, y макс – максимальные значения координат, увеличенные до большего числа, кратного 200, xмин, yмин – минимальные значения координат, измененные до меньшего числа, кратного 200, 200 – длина стороны квадрата в метрах на местности, на плане сторона квадрата равна 10 сантиметрам.
Для удобства определения максимальных и минимальных значений рекомендуется расположить выбранные значения координат на числовой оси.
Например:
xмакс = + 489,23 м, увеличиваем в большую сторону до плюс 600.
xмин = - 204,65 м, уменьшаем в меньшую сторону до минус 400.
Линии сетки квадратов подписываются значениями координат, кратными 200, ноль тоже является кратным числом.
Вершины теодолитных ходов наносят на план в соответствии со значениями координат, занесенных в ведомость замкнутого теодолитного хода, и учетом масштаба, помня, что в геодезической прямоугольной системе координат, ось абсцисс направлена с юга на север, ось ординат – с запада на восток.
Правильность нанесения двух соседних вершин проверяют по длине горизонтального проложения между ними, расхождение не должно превышать 0.2 мм плана.
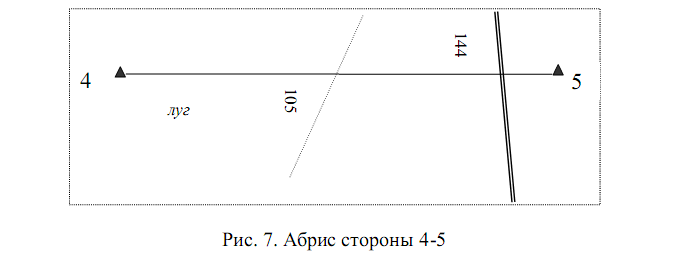
При составлении плана все расстояния, указанные на абрисах в соответствие с заданным масштабом уменьшать в 20 раз.
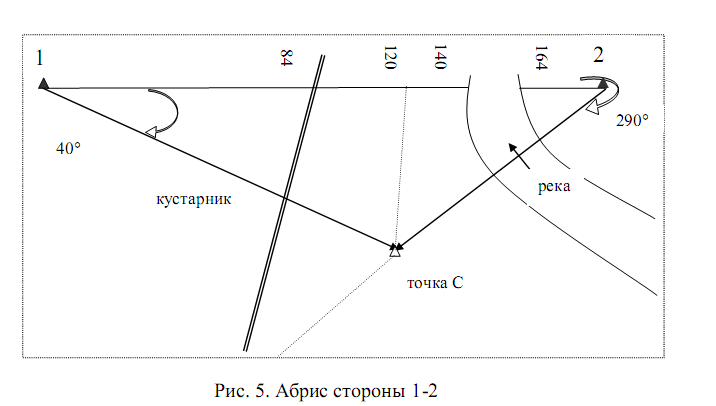
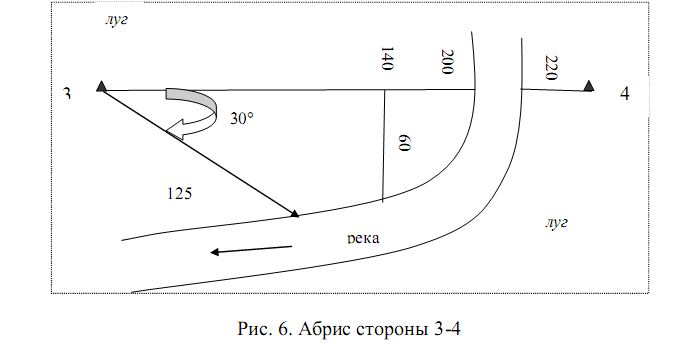
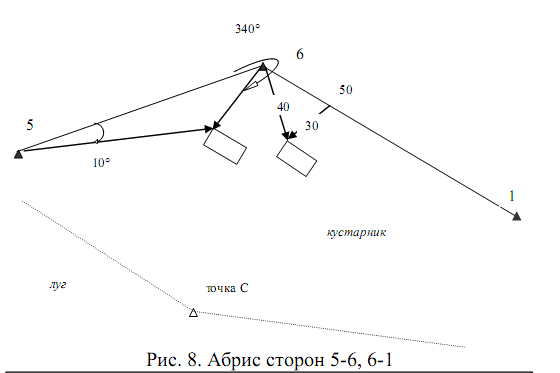
Для нанесения на план природных и искусственных объектов используют абрисы теодолитной съемки, выполненные относительно сторон теодолитных ходов (см. рис.5 – 8) и пять способов нанесения ситуации:
1. Способ перпендикуляров.
Нанесение ситуации, снятой способом перпендикуляров, начинают с определения места положения основания перпендикуляра:
для этого от младшей станции откладывают расстояние до основания перпендикуляра, оно указано на абрисе в метрах; из полученной точки восстанавливают перпендикуляр, указанной величины.
На абрисах способом перпендикуляров снята точка (140) правого берега реки.
2. Способ угловых засечек.
Центр транспортира совмещают с вершиной хода (с которой производилась съемка), ноль транспортира направляют на вершину хода, отсчет на которую по горизонтальному кругу теодолита при съемке составлял 0°0'. Отложив по транспортиру значение измеренного угла, строят первый угол; аналогично строится и второй угол. Точка пересечения сторон углов будет соответствовать местоположению рассматриваемой точки.
Этим способом сняты:
1. точка С,
2. угол жилого дома (размеры дома 10 на 15 метров).
3. Способ полярных координат.
Полярными координатами являются угол и расстояние по стороне угла до рассматриваемой точки. Угол строится как в рассмотренном выше способе, расстояние откладываем по стороне полярного угла, несовпадающей со стороной теодолитного хода; так снята точка правого берега реки.
4. Способ линейных засечек.
Для определения местоположения объекта из центров, расположенных на стороне хода, проводят дуги, радиусы которых вычисляют по формуле: R =d / 20; где d – расстояние в метрах до рассматриваемой точки, указано на абрисе, 20 – знаменатель масштаба в метрах.
Способом линейных засечек снят угол жилого дома.
5. Способ створов.
Этот способ применяют в том случае, если контуры снимаемого объекта пересекают сторону хода или когда объект расположен (пересекает) продолжение стороны хода.
Способ створов использован при определении точек пересечения сторон теодолитного хода
рекой (стороны 1-2 и 3-4),
железной дорогой (стороны 1-2 и 4-5),
границей контура луга (1-2 и 4-5).
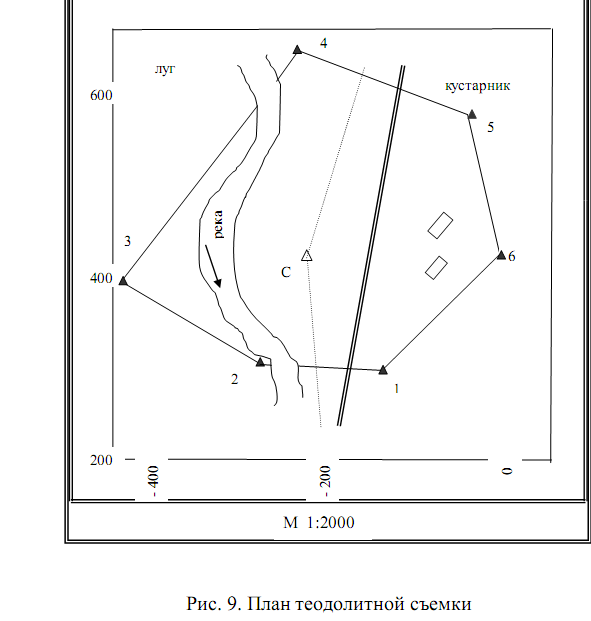
К защите расчётно-графической работы студент должен представить оформленную ручкой ведомость вычисления координат точек теодолитного хода и выполненный в карандаше план теодолитной съёмки или их компьютерные версии.