Geometria Euclidiana Plana
ÍNDICE
1 – Ângulos
1.1 – Definição
1.2 – Ângulo agudo
1.3 – Ângulo obtuso
1.4 – Ângulos opostos pelo vértice
1.5 – Ângulos suplementares
1.6 – Ângulos complementares
1.7 – Ângulos formados por duas retas paralelas interceptadas por uma transversal
2 – Triângulos
2.1 – Definição
2.2 – Elementos
2.3 – Classificação
2.4 – Soma dos ângulos de um triângulo
2.5 – Ângulo externo
2.6 – Teorema do ângulo externo
2.7 – Bissetriz de um ângulo
2.8 – Altura
3 – Congruência de triângulos
3.1 – Definição
3.2– Casos de congruência
4 – Polígonos
4.1 – Definição
4.2 – Nomenclatura
4.3 – Polígono Convexo
4.4 – Ângulos de um polígono convexo
4.5 – Ângulos internos
4.6 – Ângulos externos
4.7 – Polígono regular
4.8 – Ângulos num polígono regular
5 – Ângulos na circunferência
5.1 – Ângulo central
5.2 – Ângulo inscrito
5.3 – Ângulo de vértice interno
5.4 – Ângulo de vértice externo
5.5 – Ângulo de segmento
6 – Quadriláteros
6.1 – Definição e elementos
6.2 – Soma de ângulos interno
6.3 – Classificação
6.3.1– Paralelogramo
6.3.2– Trapézio
7 – Segmentos e Pontos Notáveis no Triângulo
7.1 – Mediana de um Triângulo
7.2 – Bissetriz
7.3 – Altura
7.4 – Mediatriz
7.5 – Teorema de Tales
7.6 – Teorema da bissetriz interna
7.7 – Teorema da bissetriz externa
8 – Semelhança de triângulos
8.1 – Definição
8.2 – Razão de semelhança
9 – Relações Métricas no Triângulo Retângulo
10 – Área das Figuras Planas
– Ângulos
1.1 – Definição
Ângulo é o nome que se dá à abertura formada por duas semi-retas que partem de um mesmo ponto.
Em que:
e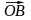
são os lados do ângulo
“O” é o vértice do ângulo.
Ângulos importantes:
|
Medida |
||
Ângulo |
Figura |
Graus |
Radianos |
Reto |
. |
90º |
π/2 rad |
Raso |
|
180º |
π rad |
de uma volta |
|
360º |
2π rad |
Observação: 1º = 60’ (1 grau = 60 minutos)
1’ = 60” (1 minuto = 60 segundos)
1) Simplifique as seguintes medidas:
a) 30º70’=
b) 110º58’300” =
c) 45º150’ =
d) 30º56’240” =
e) 65º39’123” =
2) Determine as somas:
a) 30º40’ + 15º35’ =
b) 10º30’45” + 15º29’20” =
3) Determine as diferenças:
a) 20º50’45” – 5º45’30” =
b) 31º40’ – 20º45’ =
c) 90º15’20” – 45º30’50” =
d) 90º - 50º30’45” =
4) Determine os produtos:
a) 2 x (10º35’45”) =
b) 5 x (6º15’30”) =
5) Determine as divisões:
a) (46º48’54”) ÷ 2 =
b) (31º32’45”) ÷ 3 =
c) (52º63’45”) ÷ 5 =
1.2 – Ângulo agudo
É aquele cuja medida é menor que a de um ângulo reto.
– Ângulo obtuso
É aquele cuja medida é maior que a de um ângulo reto e menor que a de um raso.
– Ângulos opostos pelo vértice
São aqueles cujos lados de um são semi-retas opostas dos lados do outro.
– Ângulos suplementares
Dois ângulos são suplementares quando a soma de suas medidas é 180º.
– Ângulos complementares
Dois ângulos são complementares quando a soma de suas medidas é 90º.
6) Determine o valor de x nos casos:
a)
b)
c)
d)
e
)
7) Determine o valor de x nos casos:
a)
b)
8) Calcule o complemento dos seguintes ângulos:
25°
47°
9) Calcule o suplemento dos seguintes ângulos:
72°
141°
10) Dado um ângulo de medida x, indique:
Seu complemento; f) A sétima parte do complemento;
Seu suplemento; g) A quinta parte do suplemento;
O dobro do seu complemento; h) O complemento da sua terça parte;
A metade do seu suplemento; i) O triplo do suplemento da sua quinta parte.
O triplo do seu suplemento;
11) Dê a medida do ângulo que vale o dobro do seu complemento.
12) Determine a medida do ângulo igual ao triplo do seu complemento.
13) Calcule o ângulo que vale ao quádruplo do seu complemento.
14) Calcule um ângulo, sabendo que um quarto do seu suplemento vale 36°.
15) Qual é o ângulo que excede o seu complemento em 76°?
16) O triplo do complemento de um ângulo, aumentado em 50°, é igual ao suplemento do ângulo. Determine a medida do ângulo.
17) Determine as medidas de dois ângulos suplementares, sabendo que o dobro de um deles, somado com a sétima parte do outro, resulta em 100°.
18) A soma de um ângulo com a terça parte do seu complemento resulta em 46°. Determine o suplemento desse ângulo.