21. Формулы сокращенного умножения.

Очень часто приведение многочлена к стандартному виду можно осуществить путём применения формул сокращённого умножения . Все они доказываются непосредственным раскрытием скобок и приведением подобных слагаемых. Формулы сокращённого умножения нужно знать наизусть:

a ²  –  b ²  = ( a  +  b )( a  –  b ), ( a  +  b ) ²  =  a ²  + 2 ab  +  b ², ( a  –  b ) ²  =  a ²  – 2 ab  +  b ², a ³  +  b ³  = ( a  +  b )( a ²  –  ab  +  b ² ), a ³  –  b ³  = ( a  –  b )( a ²  +  ab  +  b ² ), a ⁿ  –  b ⁿ  = ( a  –  b )( a ^{n  – 1}  +  a ^{n  – 2} b  +  a ^{n  – 3} b ²  + … +  ab ^{n  – 2}  +  b ^{n  – 1} ), ( a  +  b ) ³  =  a ³  + 3 a ² b  + 3 ab ²  +  b ³  =  a ³  +  b ³  + 3 ab ( a  +  b ), ( a  –  b ) ³  =  a ³  – 3 a ² b  + 3 ab ²  –  b ³  =  a ³  –  b ³  – 3 ab ( a  –  b ).

Пример 1

Докажите формулу a ³  +  b ³  = ( a  +  b )( a ²  –  ab  +  b ² ).

Показать решение

Имеем ( a  +  b )( a ²  –  ab  +  b ² ) =  a ³  –  a ² b  +  ab ²  +  ba ²  –  ab ²  –  b ³. Приводя подобные слагаемые, мы видим, что ( a  +  b )( a ²  –  ab  +  b ² ) =  a ³  +  b ³, что и доказывает нужную формулу.

Пример 2

Упростите выражение (2 x ³  – 5 z )(2 x ³  + 5 z ).

Показать решение

Воспользуемся формулой разности квадратов, получим: (2 x ³  – 5 z )(2 x ³  + 5 z ) = (2 x ³ ) ²  – (5 z ) ²  = 4 x ⁶  – 25 z ².

Ответ.  4 x ⁶  – 25 z ².

22. Арифметический квадратный корень и его свойства.

 Как мы знаем, корень чётной степени имеет два значения: положительное и отрицательное. Так,

 

Арифметическим корнем  n–й степени из неотрицательного числа  a называется неотрицательное число,  n–я степень которого равна  a .

 

Алгебраическим корнем  n–й степени из данного числа называется множество всех корней из этого числа. Алгебраический корень чётной степени имеет два значения:  положительное и отрицательное, например:

Алгебраический корень  нечётной степени имеет единственное значение: либо положительное, либо отрицательное. Например, арифметический корень

И наоборот, кубический корень:

 

Арифметический корень тесно связан с понятием абсолютной величины ( модуля ) числа, а именно:

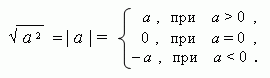
Формулы:

23. Арифметическая прогрессия. Формула общего члена и суммы первых членов.

Числовую последовательность { a _n }, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом d , называют арифметической прогрессией . Число d называется разностью арифметической прогрессии : a _{n  + 1}  =  a _n  +  d .

Так как a _{n  – 1}  =  a _n  –  d , то a _{n  + 1}  +  a _{n  – 1}  = 2 a _n . Верно и обратное.

Последовательность является арифметической тогда и только тогда, когда для любого n  > 1 выполняется рекуррентное соотношение

Формула общего члена арифметической прогрессии { a _n } такова: a _n  =  a ₁  + ( n  – 1) ·  d .

Доказательство

Докажем это пользуясь методом математической индукции. Легко убедиться, что для n  = 1 данная формула верна. Пусть эта формула верна для n  =  k . Докажем ее справедливость для n  =  k  + 1. Имеем a _{k  + 1}  =  a _k  +  d  =  a ₁  + ( k  – 1) ·  d  +  d  =  a ₁  +  k  ·  d . Теорема доказана.

Модель 1.1. Растущее дерево.

Сумма n первых членов арифметической прогрессии { a _n } равна

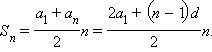
Обе формулы легко доказать, используя метод математической индукции. Выполните это самостоятельно.