16. Одночлен. Подобные одночлены.

17. Сложение, вычитание, умножение и деление одночленов.

Алгебраическое выражение − это выражение, составленное из чисел и переменных с помощью знаков сложения, вычитания, умножения, деления, возведения в рациональную степень и извлечения корня и скобок.

Простейшим алгебраическим выражением является одночлен.

Одночленом называется выражение, которое содержит числа, натуральные степени переменных и их произведения, и при этом не содержит никаких других действий с этими числами и переменными. Например, 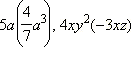− одночлены, а выражения 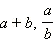− не одночлены.

Одночлен называется представленным в стандартном виде , если он представлен в виде произведения числового множителя на первом месте и степеней различных переменных. Числовой множитель у одночлена стандартного вида называется коэффициентом одночлена , сумму показателей степени переменных называют степенью одночлена . Ясно, что произведение одночленов также будет одночленом; ясно также, что одночлен в некоторой натуральной степени также является одночленом. Результаты таких действий (умножение одночленов и возведение одночлена в степень) обычно приводят к стандартному виду.

Пример 1

Привести к стандартному виду одночлены: 1) 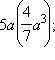2)

Показать решение

1)

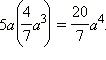
2) 4 xy ² (–3 xz ) = –12 x ² y ² z .

Ответ. 1) 2)

Два одночлена, приведённых к стандартному виду, называются подобными , если они совпадают или же отличаются только числовым коэффициентом. Сложение и вычитание подобных одночленов называется приведением подобных слагаемых .

Пример 2

Привести подобные члены в выражении

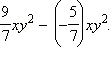
Показать решение

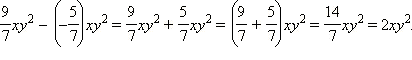
Ответ.  2 xy ².

18. Многочлен. Сложение и вычитание многочленов.

19. Умножение и деление многочлена на одночлен.

20. Умножение многочленов.

Многочленом называется сумма одночленов. Если все одночлены в многочлене приведены к стандартному виду, то говорят, что это многочлен стандартного вида . Алгебраическое выражение, не содержащее операции деления и извлечения корня (такое выражение называется целым ), всегда может быть приведено к многочлену стандартного вида. Степенью многочлена называется наибольшая из степеней его слагаемых.

Пример 3

Привести к многочлену стандартного вида ( a  –  b )( a  +  b ).

Показать решение

Имеем ( a  –  b )( a  +  b ) = ( a  –  b ) ·  a  + ( a  –  b ) ·  b  =  a ²  –  ba  +  ba  –  b ²  =  a ²  –  b ².

Ответ.   a ²  –  b ².

Пример 4

Привести к многочлену стандартного вида ( a ²  –  ab ) – (3 ab  – 2 a ²  – 5 b ( a  +  b ² )).

Показать решение

( a ²  –  ab ) – (3 ab  – 2 a ²  – 5 b ( a  +  b ² )) =  a ²  –  ab  – 3 ab  + 2 a ²  + 5 ba  + 5 b ³  = 3 a ²  +  ab  + 5 b ³.

Ответ.  3 a ²  +  ab  + 5 b ³.

Часто бывает полезно преобразовать многочлен так, чтобы он был представлен в виде произведения нескольких сомножителей. Такое тождественное преобразование называется разложением многочлена на множители . В этом случае говорят, что многочлен делится на каждый из этих сомножителей. При разложении многочленов на множители применяют три основных приёма: вынесение множителя за скобку, использование формул сокращённого умножения и способ группировки.

1. Вынесение множителя за скобку. Из распределительного закона непосредственно следует, что ac  +  bc  =  c ( a  +  b ). Этим можно воспользоваться для вынесения множителя за скобки.

Пример 1

Разложить многочлен на множители 12 y ³  – 20 y ².

Показать решение

Имеем: 12 y ³  – 20 y ²  = 4 y ²  · 3 y  – 4 y ²  · 5 = 4 y ² (3 y  – 5).

Ответ.  4 y ² (3 y  – 5).

2. Использование формул сокращённого умножения. Формулы сокращённого умножения позволяют довольно эффективно представлять многочлен в форме произведения.

Пример 2

Разложить на множители многочлен x ⁴  – 1.

Показать решение

Имеем: x ⁴  – 1 = ( x ² ) ²  – 1 ²  = ( x ²  – 1)( x ²  + 1) = ( x ²  – 1 ² )( x ²  + 1) = ( x  + 1)( x  – 1)( x ²  + 1).

Ответ.  ( x  + 1)( x  – 1)( x ²  + 1).

3. Способ группировки. Этот способ заключается в том, что слагаемые многочлена можно сгруппировать различными способами на основе сочетательного и переместительного законов. На практике он применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку и исходный многочлен окажется представленным в виде произведения.

Пример 3

Разложить на множители многочлен x ³  – 3 x ² y  – 4 xy  + 12 y ².

Показать решение

Сгруппируем слагаемые следующим образом: x ³  – 3 x ² y  – 4 xy  + 12 y ²  = ( x ³  – 3 x ² y ) – (4 xy  – 12 y ² ). В первой группе вынесем за скобку общий множитель x ², а во второй − 4 y . Получаем: ( x ³  – 3 x ² y ) – (4 xy  – 12 y ² ) =  x ² ( x  – 3 y ) – 4 y ( x  – 3 y ). Теперь общий множитель ( x  – 3 y ) также можно вынести за скобки: x ² ( x  – 3 y ) – 4 y ( x  – 3 y ) = ( x  – 3 y )( x ²  – 4 y ).

Ответ.  ( x  – 3 y )( x ²  – 4 y ).