64. Треугольник и его элементы.

Треугольником называется фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих эти точки попарно. Точки называются вершинами , а отрезки – сторонами треугольника.

Углом треугольника   ABC (треугольник обозначается Δ  ABC ) при вершине A (или углом между сторонами AB и AC ) называется угол, образованный лучами AB и AC ; A  =  BAC  =  CAB . Внешним углом треугольника при данной вершине называется угол, смежный с углом треугольника при этой вершине.

Рисунок 4.1.1.

Треугольник называется разносторонним , если любые две стороны его не равны друг другу. Треугольник, все стороны которого равны, называется равносторонним .

Треугольник называется остроугольным , если все его углы острые. Треугольник называется тупоугольным , если один из его углов тупой.

Два треугольника называются равными  ( Δ  ABC  = Δ  A ₁ B ₁ C ₁ ), если у них соответствующие стороны равны и соответствующие углы равны .

65. Признаки равенства треугольников.

Теорема 4.1. 

Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Доказательство

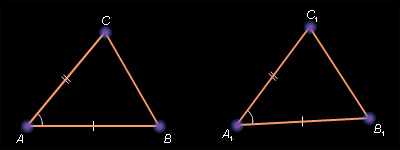Рисунок 4.2.1.

Пусть Δ  ABC и таковы, что     (рис. 4.2.1). В соответствии с аксиомой 4.1 существует равный данному с вершиной в точке с вершиной лежащей на луче и вершиной в той же полуплоскости относительно прямой где лежит вершина (рис. 4.2.2).

Так как по условию, то на основании аксиомы 1.5 точки и совпадают (рис. 4.2.3).

Так как то луч совпадает с лучом (рис. 4.2.4). Так как то на основании аксиомы 2.5 вершина совпадает с вершиной (рис. 4.2.5). Тогда совпадает с и, значит, равен Δ  ABC . Теорема доказана.

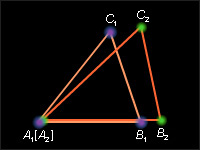Рисунок 4.2.2.

Рисунок 4.2.3.

Рисунок 4.2.4.

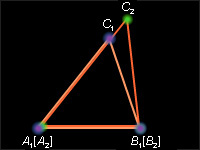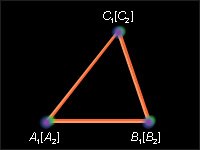Рисунок 4.2.5. Таблица 4.2.1.

Теорема 4.2. 

Второй признак равенства треугольников. Если сторона и прилежащие к ней углы одного треугольника равны соответственно стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.

Доказательство

Пусть Δ  ABC и таковы, что     По аксиоме 4.1 существует равный Δ  ABC , с вершиной на луче и с вершиной в той же полуплоскости, где и вершина Так как то вершина совпадает с вершиной Так как и то луч совпадает с лучом а луч совпадает с лучом Отсюда следует, что вершина совпадает с вершиной Итак, совпадает с треугольником а значит, равен Δ  ABC . Теорема доказана. (рис. 4.2.6).

Рисунок 4.2.6.

Теорема 4.7. 

Третий признак равенства треугольников. Если три стороны одного треугольника равны соответственно трем сторонам другого треугольника, то такие треугольники равны.

Рисунок 4.3.2.

Доказательство

Пусть Δ  ABC и Δ  A ₁ B ₁ C ₁ таковы, что AB  =  A ₁ B ₁ ; BC  =  B ₁ C ₁ ; AC  =  A ₁ C ₁. Доказательство от противного.

Пусть треугольники не равны. Отсюда следует, что одновременно. Иначе треугольники были бы равны по первому признаку.

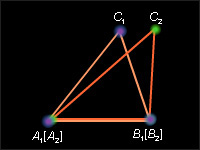
Пусть Δ  A ₁ B ₁ C ₂ – треугольник, равный Δ  ABC , у которого вершина C ₂ лежит в одной полуплоскости с вершиной C ₁ относительно прямой A ₁ B ₁. По предположению вершины C ₁ и C ₂ не совпадают. Пусть D – середина отрезка C ₁ C ₂. Треугольники A ₁ C ₁ C ₂ и B ₁ C ₁ C ₂ – равнобедренные с общим основанием C ₁ C ₂. Поэтому их медианы A ₁ D и B ₁ D являются высотами. Значит, прямые A ₁ D и B ₁ D перпендикулярны прямой C ₁ C ₂. A ₁ D и B ₁ D имеют разные точки A ₁ и B ₁, следовательно, не совпадают. Но через точку D прямой C ₁ C ₂ можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию. Теорема доказана.

Рисунок 4.3.3.