Второй признак: Если две стороны одного треугольника пропорциональны двум сторонам другого и углы между этими сторонами равны, то треугольники подобны.

Дано: ∆ABC и ∆A₁B₁C₁, A= A₁, = .

Доказать: ∆ABC ∆A₁B₁C₁.

Доказательство

1) Рассмотрим ∆ABC₂, в котором BAC₂= A₁ и ∠ABC₂=∠B₁:

∆ABC₂ ∆A₁B₁C₁ (первый признак) => = .

2) По условию:

= => AC=AC₂ => ∆ABC = ∆ABC₂ (первый признак) => B= ABC₂=∠B₁ => ∆ABC ∆A₁B₁C₁ (первый признак).

Теорема доказана.

Третий признак: Если три стороны одного треугольника пропорциональны трем сходственным сторонам другого, то треугольники подобны.

Дано: ∆ABC и ∆A₁B₁C₁, = = .

Доказать: ∆ABC ∆A₁B₁C₁.

Доказательство

1) Рассмотрим ∆ABC₂, в котором BAC₂= A₁ и ABC₂= B₁:

∆ABC₂ ∆A₁B₁C₁ (первый признак) => = = .

2) По условию:

= = => AC=AC₂, BC=BC₂ => ∆ABC = ∆ABC₂ (третий признак); ∆ABC₂ ∆A₁B₁C₁ => ∆ABC ∆A₁B₁C₁.

Теорема доказана.

59. Свойство серединного перпендикуляра к отрезку.

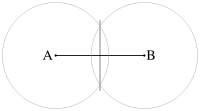
Серединный перпендикуляр — прямая, перпендикулярная к данному отрезку и делящая его на две равные части. Любая точка этой прямой равноудалена от концов данного отрезка.

Серединные перпендикуляры к сторонам треугольника или другого описываемого окружностью многоугольника пересекаются в одной точке — центре описанной окружности.

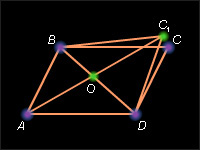
60. Параллелограмм. Свойство диагоналей параллелограмма.

Теорема 7.5. 

Диагонали параллелограмма пересекаются и точкой пресечения делятся пополам.

Доказательство

Пусть ABCD – данный параллелограмм. По определению ( AB ) || ( CD ) и ( AD ) || ( BC ). Пусть O – середина диагонали BD и на луче, дополняющем луч OA , отложен отрезок OC ₁, равный отрезку OA . По теореме 7.1 получившийся четырехугольник ABC ₁ D – параллелограмм, и, следовательно, ( BC ₁ ) || ( AD ) и ( AB ) || ( C ₁ D ). С учетом условия – ( BC ) || ( AD ) и ( AB ) || ( CD ). В соответствии с теоремой 3.3 ( BC ) = ( BC ₁ ) и ( DC ) = ( DC ₁ ). Поэтому точки C и C ₁ совпадают. Следовательно, совпадают параллелограммы ABCD и ABC ₁ D . Отсюда AO  =  OC и BO  =  OD . Теорема доказана.

Рисунок 7.2.5.

61. Ромб. Свойства диагоналей ромба.

Ромбом называется параллелограмм, у которого все стороны равны.

Рисунок 7.3.1.

Свойства ромба.

Теорема 7.8. 

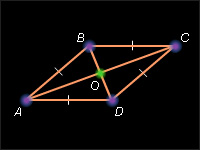
Диагонали ромба пересекаются под прямым углом.

Доказательство

Пусть ABCD – данный ромб. Рассмотрим треугольник ABD . AB  =  AD по условию, и, следовательно, Δ  ABD равнобедренный. Так как ABCD – параллелограмм, то BO  =  OD . Тогда AO – медиана и по теореме 4.4  AO – высота в треугольнике BAD . Следовательно, ( AC )   ( BD ) .

Рисунок 7.3.2.

Теорема 7.9. 

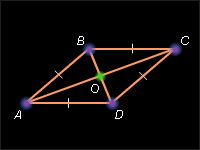
Диагонали ромба являются биссектрисами его углов.

Доказательство

Пусть ABCD – данный ромб. Рассмотрим треугольник ABD . AB  =  AD по условию, и, следовательно, Δ  ABD – равнобедренный. Так как ABCD – параллелограмм, то BO  =  OD . Тогда AO – медиана и по теореме 4.4 AO – биссектриса в треугольнике BAD . Следовательно, BAO  =  DAO . Аналогично, рассмотрев треугольник ABC , получаем, что BO – медиана в равнобедренном треугольнике ABC , и, следовательно, BO – биссектриса угла ABC . Теорема доказана.

Рисунок 7.3.3.

Признаки ромба.

Теорема 7.10. 

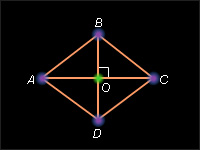
Если диагонали параллелограмма перпендикулярны, то параллелограмм – ромб.

Доказательство

Пусть ABCD – данный параллелограмм, AC и BD – его диагонали и ( AC )   ( BD ). Пусть O – точка пересечения диагоналей параллелограмма. Треугольник ABC – равнобедренный с основанием AC . Действительно, так как диагонали параллелограмма в точке пересечения делятся пополам, то AO  =  OC , и тогда BO – медиана треугольника ABC , проведенная к стороне AC . Но по условию ( BO )   ( AC ) и [ BO ] – высота треугольника ABC . Тогда по теореме 4.6  ABC – равнобедренный треугольник с основанием AC . Отсюда – AB  =  BC . По свойству равенства противоположных сторон параллелограмма (теорема 7.3) следует, что AB  =  BC  =  CD  =  AD . Таким образом, данный параллелограмм – ромб. Теорема доказана.

Рисунок 7.3.4.

Теорема 7.11. 

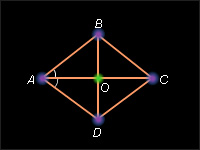
Если диагональ параллелограмма является биссектрисой его угла, то параллелограмм – ромб.

Доказательство

Пусть ABCD – данный параллелограмм, AC – его диагональ и, при этом, AC – биссектриса угла A параллелограмма. Так как AC – биссектриса угла A , то BAC  =  CAD . С другой стороны, углы CAD и BCA внутренние накрест лежащие при параллельных прямых BC и AD и секущей AC и по теореме 3.4 BCA  =  CAD . Отсюда BAC  =  BCA и по признаку равнобедренного треугольника (теорема 4.5) ABC равнобедренный, и, следовательно, AB  =  BC . Так как ABCD – параллелограмм, то AB  =  CD , BC  =  AD . Тогда AB  =  BC  =  CD  =  AD . Таким образом, ABCD – ромб. Теорема доказана.

Рисунок 7.3.5.