48. Теорема Фалеса.

Две пары параллельных прямых, отсекающие на одной секущей равные отрезки, отсекают на любой другой секущей также равные отрезки.

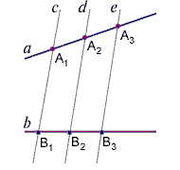Согласно теореме Фалеса (см. рисунок), если A₁A₂ = A₂A₃, то B₁B₂ = B₂B₃.

В теореме нет ограничений на взаимное расположение секущих (она верна как для пересекающихся прямых, так и для параллельных). Также неважно, где находятся отрезки на секущих.

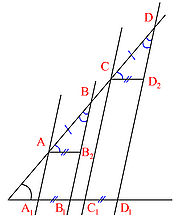
Доказательство в случае секущих  

Рассмотрим вариант с несвязанными парами отрезков: пусть угол пересекают прямые AA₁ | | BB₁ | | CC₁ | | DD₁ и при этом AB = CD.

1) Проведём через точки A и C прямые, параллельные другой стороне угла. Получим два параллелограмма AB₂B₁A₁ и CD₂D₁C₁. Согласно свойству параллелограмма: AB₂ = A₁B₁ и CD₂ = C₁D₁.

2) Треугольники и равны на основании второго признака равенства треугольников:

AB = CD согласно условию теоремы,

как соответственные, образовавшиеся при пересечении параллельных BB₁ и DD₁ прямой BD.

Аналогично каждый из углов и оказывается равным углу с вершиной в точке пересечения секущих.

3)A₁B₁ = C₁D₁ как соответственные элементы в равных треугольниках■

Доказательство в случае параллельных прямых  

Проведем прямую BC. Углы ABC и BCD равны как внутренние накрест лежащие при параллельных прямых AB и CD и секущей BC, а углы ACB и CBD равны как внутренние накрест лежащие при параллельных прямых AC и BD и секущей BC. Тогда по первому признаку равенства треугольников треугольники ABC и DCB равны. Отсюда следует, что AC = BD и AB = CD.

49. Параллельные прямые.

Две прямые называются параллельными , если они не пересекаются.

Для обозначения параллельности прямых будем пользоваться символом ||.

Определяющее свойство задается аксиомой:

Аксиома 3.1. 

Через точку, не лежащую на данной прямой, можно провести прямую, параллельную данной, и притом только одну.

Для описания свойств параллельных прямых, вытекающих из определения и аксиомы 3.1, введем новые понятия и утверждения, связанные с взаимным расположением трех прямых на плоскости.

Прямая AC называется секущей по отношению к прямым AB и CD , если она пересекает обе прямые. Если прямая AC является секущей по отношению к прямым AB , CD и, кроме того, точки B и D лежат в одной полуплоскости от секущей AC , то углы BAC и DCA называются внутренними односторонними . Если AC – секущая по отношению AB и CD , а точки B и D лежат в разных полуплоскостях от AC , то углы BAC и DCA называются внутренними накрест лежащими .

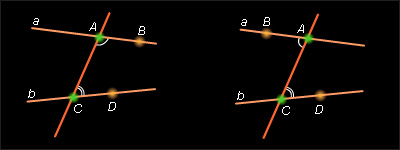Рисунок 3.1.1.

Если в данной паре внутренних накрест лежащих углов один из углов заменить на вертикальный ему, то полученные углы называются соответственными углами данных прямых с секущей.

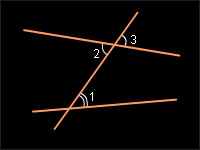Рисунок 3.1.2.

50. Признак параллельности прямых (по внутренним накрест лежащим углам).

Cледующая теорема дает достаточные условия параллельности (т.е. условия, выполнение которых гарантирует параллельность) двух прямых. Иначе такую теорему можно назвать признаком параллельности прямых:

Теорема 3.1. 

Если внутренние накрест лежащие углы равны, то прямые параллельны.

Доказательство

До ознакомления с доказательством теоремы 3.1 необходимо изучить раздел 4.1 и теоремы 4.1 и 4.2 главы 4. Докажем теорему так называемым методом от противного: предположим, что условие теоремы выполнено, а именно: прямые AB и CD образуют с секущей AC равные внутренние накрестлежащие углы, но вопреки утверждению теоремы прямая AB не паралельна прямой CD и, следовательно, они пересекаются в точке O , которая лежит в одной из полуплоскостей от прямой AC .

Рисунок 3.2.1.

Отложим от луча А C треугольник  AO ₁ C , равный CO А, так, что вершина O ₁ лежит в другой, нежели точка O , полуплоскости. Из равенства этих треугольников следует, что , ; по условию: и тогда точки O , C , лежат на одной прямой, и, аналогично, из равенства по условию углов OCA и смежного к BAC следует, что точки O ₁,  A ,  O лежат также на одной прямой. Отсюда следует, что через две различные точки O и O ₁  плоскости проходят две различные прямые AB и CD . Это противоречит аксиоме 1.2. Полученное противоречие доказывает теорему.

На основании теоремы 3.1 можно легко доказать еще несколько признаков параллельности.

Если соответственные углы равны, то прямые параллельны.

Если сумма внутренних односторонних углов равна 180°, то прямые параллельны.

Из данного утверждения вытекает

Следствие 3.1. 

Две прямые, перпендикулярные третьей, параллельны.