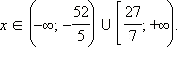- •Натуральные числа и действия над ними.
- •Делители и кратные. Признаки делимости.
- •Простые числа. Разложение числа на простые множители.
- •Разложение числа на простые множители.
- •Нод и нок числа.
- •Обыкновенные дроби.
- •Обыкновенные дроби. Основное свойство дроби.
- •Сокращение дробей.
- •Арифметические действия с обыкновенными дробями.
- •Отношения. Пропорции. Основное свойство пропорции.
- •Степень с натуральным показателем.
- •Умножение и деление степеней с одинаковым основанием.
- •Возведение степени в степень.
- •Возведение в степень произведения и частного.
- •Одночлен. Подобные одночлены.
- •Сложение, вычитание, умножение и деление одночленов.
- •Многочлен. Сложение и вычитание многочленов.
- •Умножение и деление многочлена на одночлен.
- •Умножение многочленов.
- •Формулы сокращенного умножения.
- •Арифметический квадратный корень и его свойства.
- •Формулы:
- •Арифметическая прогрессия. Формула общего члена и суммы первых членов.
- •Геометрическая прогрессия. Формула общего члена и суммы первых членов.
- •Уравнение с одной переменной. Корни уравнения.
- •Линейное уравнение.
- •Квадратное уравнение.
- •Формула корней квадратного уравнения.
- •Теорема Виета.
- •Разложение квадратного трехчлена на множители.
- •Система уравнений. Решение системы двух линейных уравнений с двумя переменными.
- •Числовые неравенства и их свойства.
- •Линейные неравенства с одной переменной и их системы.
- •Функция. Область определения и область значений.
- •График и свойства функции .
- •График и свойства функции .
- •График и свойства функции
- •График и свойства функции .
- •Свойства квадратичной функции
- •Окружность, вписанная в треугольник.
- •Вектор. Умножение вектора на число. Скалярное произведение векторов.
- •Окружность, описанная около треугольника.
- •Многоугольник. Правильный многоугольник.
- •Сумма углов выпуклого многоугольника.
- •Средняя линия треугольника и ее свойства.
- •Площадь параллелограмма.
- •Теорема Фалеса.
- •Параллельные прямые.
- •Признак параллельности прямых (по внутренним накрест лежащим углам).
- •Подобие треугольников. Признак подобия треугольников по трем сторонам.
- •Теорема о двух прямых, параллельных третьей прямой.
- •Определение тригонометрических функций острого угла.
- •Внешний угол треугольника и его свойство.
- •Теорема о двух перпендикулярах к одной прямой.
- •Прямоугольный треугольник. Теорема Пифагора.
- •Подобие треугольников.
- •Признак подобия треугольников.
- •Первый признак Если два угла одного треугольника соответственно равны двум углам другого, то треугольники подобны.
- •Второй признак: Если две стороны одного треугольника пропорциональны двум сторонам другого и углы между этими сторонами равны, то треугольники подобны.
- •Свойство серединного перпендикуляра к отрезку.
- •Параллелограмм. Свойство диагоналей параллелограмма.
- •Ромб. Свойства диагоналей ромба.
- •Окружность. Касательная к окружности и ее свойства.
- •Сумма углов треугольника.
- •Треугольник и его элементы.
- •Признаки равенства треугольников.
- •Длина окружности. Площадь круга.
- •Вектор. Сумма и разность векторов. Координаты вектора.
- •Свойства равнобедренного треугольника.
- •Параллелограмм. Признак параллелограмма.
- •Параллелограмм. Свойства противоположных сторон и углов параллелограмма.
- •Трапеция. Средняя линия трапеции и ее свойства.
- •Биссектриса угла и ее свойства.
- •Площадь треугольника.
- •Прямоугольник. Свойства прямоугольника и его диагоналей.
- •Площадь трапеции.
- •Угол. Виды углов.
- •Смежные и вертикальные углы и их свойства.
Числовые неравенства и их свойства.
Неравенство - одно из фундаментальных понятий математики.
Если два вещественных
числа
a и b соединены знаком неравенства ≠ или
одним из отношений порядка a > b, или a
< b , или a![]() b,
или же a
b,
или же a![]() b
, установленных между числами, то говорят,
что задано числовое неравенство.
b
, установленных между числами, то говорят,
что задано числовое неравенство.
Неравенства отношений >,< называют строгими,неравенства , называют нестрогими.
Неравенства отношений < и , а так же неравенства > и называются неравенствами одного знака (одного смысла), неравества < и >, а так же > и ,< и , и называются неравенствами разного смысла (разного знака)
Среди свойств числовых неравенств выделяют следующие:
a > b, тогда b < a. Верно и обратное
Если a > b и b > c, то a > с
Если a > b, то для любого с a + c > b + c. Верно и обратное
Если a > b, то для любого с > 0 ac > bc. Верно и обратное
Если a > b, то для любого с < 0 ac < bc. Верно и обратное
Если a > b и c > d, то a + c > b + d (Возможность почленного сложения неравенств одинакового смысла)
Если a > b и c < d , то a - c > b — d (Возможность почленного вычитания неравенств разного смысла)
Если a > b, b 0 и c > d, d 0 , то ac > bd (Возможность почленного умножения неравенств одинакового смысла)
Если a > b, b 0 и c < d , d > 0 ,то a / c > b / d (Возможность почленного деления неравенств разного смысла)
Если a, b 0 то для любого натурального n справедливо
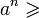 bn
(Возможность почленного умножения n
одинаковых неравенств неотрицательных
чисел)
bn
(Возможность почленного умножения n
одинаковых неравенств неотрицательных
чисел)
Пример 1
Равносильны ли
неравенства
![]()
Показать решение
Неравенства
неравносильны. Действительно,
![]()
Неравенство x + 3 < 5 будет верным и тогда, когда x + 3 < –5, например, при x = –100. Первое же неравенство при x = –100 неверно.
Ответ. Нет.
Пример 2
Равносильны ли
неравенства
![]() и
и
![]()
Показать решение
Неравенства
неравносильны. В самом деле,
![]()
Значит, множеством решений первого неравенства являются область x ≥ 0, а второго x > –1. Поскольку это разные множества, то неравенства неравносильны.
Ответ. Нет.
Линейные неравенства с одной переменной и их системы.
Говорят, что несколько неравенств образуют систему , если нужно найти все общие решения данных неравенств. Решением системы неравенств называется число, которое при его подстановке в систему обращает каждое неравенство в верное числовое неравенство. Традиционно неравенства системы объединяются фигурной скобкой.
Пример 1
Решите систему
неравенств
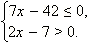
Показать решение
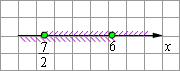
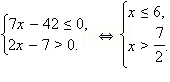 С
помощью координатной прямой находим,
что
С
помощью координатной прямой находим,
что
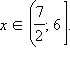
 1
1
Ответ.
Говорят, что несколько неравенств с одной переменной образуют совокупность , если необходимо найти все такие значения переменной, каждое из которых является решением хотя бы одного из данных неравенств. Традиционно совокупность неравенств обозначается квадратной скобкой.
Пример 2
Решите совокупность
неравенств
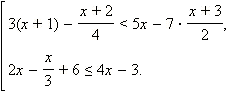
Показать решение
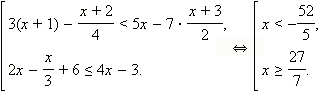 Для
решения совокупности неравенств нужно
взять все x ,
которые удовлетворяют хотя бы одному
из данных неравенств. Значит,
Для
решения совокупности неравенств нужно
взять все x ,
которые удовлетворяют хотя бы одному
из данных неравенств. Значит,
Ответ.