34.Наближення часу релаксації.

Час релаксації - період часу, за який збурення у виведеній із рівноваги фізичній системі зменшується в e разів (e - основа натуральних логарифімів).

Здебільшого позначається τ й має розмірність часу.

Згідно з принципом Лешательє-Брауна при відхилені фізичної системи від стану стійкої рівноваги виникають сили, які намагаються повернути системи до рівноважного стану. Якщо в стані рівноваги певна фізична величина f має значення f₀, причому відхилення від рівноваги , то в першому наближенні можна вважати, що ці сили пропорційні відхиленню. Кінетичне рівняння для величини f запишеться у вигляді

,

де λ - певний параметр, а знак мінус вказує на те, що реакція системи на збурення приводить до повернення до рівноважного стану.

Величина

В такому випадку величина f змінюватиметься згідно із законом:

,

де Δf₀ = f(0) − f₀ - початкове збурення.

Наближення часу релаксації широко використовується при описі кінетичних процесів у фізиці, коли мова йде про кінетику встановлення рівноважного стану. Перехід від нерівноважного стану до рівноваги супроводжується дисипацією енергії і є незворотнім процесом. Встановлення рівноваги часто проходить кілька етапів, які характеризуються своїми окремими часами релаксації. Так, при збудженні молекул світлом встановлення теплової рівноваги відбувається за часи порядку 10 ^{− 12} с, а от люмінесценція - випромінювання світла збудженими станами може мати характерні часи порядку наносекунд і навіть мікросекунд.

При описі багатьох фізичних процесів час релаксації береться як феноменологічний параметр, проте в окремих випадках його можна визначити через параметри мікроскопічних процесів, таких як ймовірність квантовомеханічного переходу чи переріз розсіювання.

35.Рівняння Шредінгера для кристала. Адіабатичне наближення розв’язку рівняння Шредінгера.

На відміну від макроскопічних тіл, мікрочастинки, якими є ядра і електрони, володіють специфічними властивостями. Тому стан електронів і ядер у кристалі потрібно описувати у рамках уявлень квантової механіки – науки про рух і взаємодію мікрочастинок. Одним з основних її положень є твердження про існування стаціонарних станів мікрочастинок та їх систем. Стаціонарні стани системи мікрочастинок, описуються рівнянням Шредінґера

(3.1)

до складу якого входять оператор Гамільтона (або, коротко, – гамільтоніан), енергія Е та функція стану Ψ. Взагалі кажучи, стаціонарних станів мікросистеми може бути багато і у будь-який момент часу вона з певною ймовірністю може знаходитись в кожному з них. Цей факт є наслідком прояву мікрочастинками хвильових властивостей; тому функцію стану часто називають хвильовою функцією. Ймовірність знаходження мікрочастинки (системи) у околі точки простору у стані з хвильовою функцією Ψ дорівнює , де – об’єм вказаного околу. З цього випливає, що має зміст щільності просторового розподілу ймовірності стану, що описується функцією Ψ. Крім того, якщо існування мікрочастинки – достовірна подія, то

(3.2)

(інтегрування здійснюється по усьому простору). Рівність (3.2) називають умовою нормування, а функцію, що її задовольняє – нормованою.

Очевидно (3.1) є рівнянням, з якого можна визначити енергію Е стаціонарного стану системи мікрочастинок, а гамільтоніан має зміст оператора енергії. Дійсно, якщо функція стану відома, то, згідно (3.1), результат дії на неї оператора Гамільтона дорівнює добутку цієї функції на величину енергії системи у цьому стані.

Якщо не цікавитись процесами, де істотними є ядерні перетворення, існування спіну ядер і електронів, а також релятивістські ефекти, то повна енергія кристалу, як системи електронів і ядер, являє собою суму

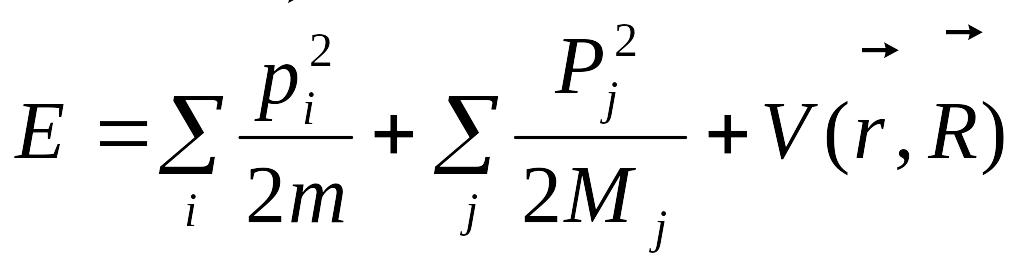, (3.3)

кінетичних енергій руху усіх електронів і ядер та потенціальної енергії їх взаємодії

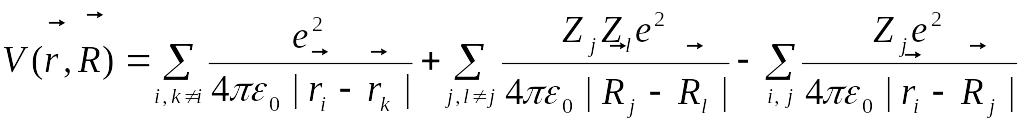. (3.4)

Тут індекси підсумовування i та j є номерами мікрочастинок; ( , ) і ( , ) – радіус-вектор та імпульс i-го електрона і j-го ядра з зарядовим числом Z_j; m і M_j – їх маси, а символами та позначено множини координат усіх, відповідно, електронів і ядер.

Згідно положень квантової механіки оператор енергії системи мікрочастинок будується з функції, що описує її повну енергію шляхом заміни вектора імпульсу кожної з них відповідним оператором імпульсу . Тоді гамільтоніан кристалу можна подати у вигляді суми

. (3.5)

Розв’язок рівняння Шредінґера (3.1) з гамільтоніаном (3.5) дає, в принципі, відповідь на питання про закономірності руху електронів та вигляд їх енергетичного спектру. А це дає змогу пояснити велику кількість явищ та властивостей твердих тіл, таких як електричні, магнітні оптичні і т.д. Проте, на кожний м³ об’єму будь-якого твердого тіла припадає близько 10²⁶ частинок, тому хвильова функція, що входить до рівняння (3.1), залежить від величезної кількості змінних. Тому знайти її явний вигляд практично неможливо. Цей факт приводить до необхідності використовувати певні наближення, які дозволили б спростити задачу пошуку розв’язку рівняння (3.1).

Першим з них є так зване адіабатичне наближення, яке полягає у нехтуванні впливу теплового руху атомів на характер руху електронів. Як свідчать оцінки величини енергії руху електрона у кристалі, його швидкість набагато перевищує швидкість руху ядер. Тому за будь-якої зміни положень ядер у системі електронів практично миттєво встановлюється такий їх просторовий розподіл, який відповідає новому положенню ядер. Іншими словами, важка і повільна система ядер неістотно змінює характер руху легкої системи швидких електронів.

У цьому випадку при вивченні руху електронів ядра можна вважати нерухомими, закріпленими у вузлах кристалічної ґратки, а кінетичною енергією ядер (другий доданок у (3.5)) – знехтувати. Крім того, відносна незалежність руху систем електронів і ядер дозволяє функцію стану кристалу подати у вигляді добутку

(3.6)

хвильової функції системи електронів на хвильову функцію системи ядер . Хвильова функція електронів у цьому випадку залежить від координат електронів; координати ядер вважаються фіксованими параметрами, про що свідчить їхня позначка .

У рамках адіабатичного наближення задача про рух електронів і ядер у кристалі істотно спрощується. Дійсно, підстановка (3.6) у рівняння Шредінґера з гамільтоніаном (3.5) дозволяє замінити рівняння (3.1) з величезною кількістю змінних ( , ) на систему двох рівнянь

(3.7)

кожне з яких містить координати мікрочастинок тільки одного типу (електронів або ядер). Тут

(3.8)

– гамільтоніан системи електронів, а

(3.9)

– ядер.

Кожне з рівнянь системи (3.6) дозволяє, в принципі, знайти енергію Е_е системи електронів, що рухаються в усередненому полі ядер, зафіксованих

у вузлах ґратки, або системи ядер – Е_я, так що енергія кристала Е = Е_е + Е_я.