32.Ефективна маса носіїв струму.

Повтор.

33.Рівняння Больцмана.

Рівняння Больцмана або кінетичне рівняння Больцмана- рівняння для опису еволюції розподілу частинок нерівноважної термодинамічної системи в просторі координат за швидкостями.

Людвіг Больцман запропонував це рівняння для опису нерівноважних газів, але воно стало широко вживатися й для електронного газу твердих тіл, оскільки дозволяє легко врахувати особливості квантової статистики Фермі-Дірака. Для просторово неоднорідної системи рівняння Больцмана дозволяє розраховувати процеси дифузії частинок. Для системи у зовнішних полях рівняння Больцмана дозволяє визначити баланс між прискоренням частинок полями й дисипацією їхньої енергії під час зіткнень.

Для опису нерівноважної термодинамічної системи вводиться залежна від часу t, просторових координат й швидкості частинок функція розподілу , яка задає ймовірність того, що частинка в момент часу t матиме перебуватиме в кубі з вершиною в точці і стороною , а її швидкість буде в діапазоні від до . Для цієї функції справедливе рівняння:

,

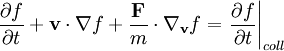де m - маса частинок, - сума зовнішних сил, які діють на ці частинки.

Зміна функції розподілу, тобто ймовірності того, що частинка перебуватиме в околі певної точки й матиме певну швидкість, відбувається

• завдяки вильоту частинки із об'єму

• завдяки прискоренню чи сповільненню, викликаному дією зовнішніх сил

• завдяки зіткненню із іншими частинками.

Член в правій частині рівняння Больцмана 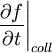описує зміну функції розподілу при зіткненнях і називається інтергралом зіткнень. При цьому детальна механіка розсіювання частинок не розглядається. Вважається, що при розсіюванні частинки миттєво міняють свої швидкості.

Рівняння Больцмана справедливе для полів, які не дуже швидко міняються в просторі. Вважається, що кожен елементрарний об'ємчик досить великий, щоб для нього можна було ввести функцію розподілу, але малий в порівнянні із характерною довжиною зміни зовнішних полів.

Рівняння Больцмана нехтує узгодженим рухом частинок. Його справедливість обмежена газами, в яких зіткнення відбуваються не дуже часто. В випадку більших густин частинок застосовуються складніші рівняння, наприклад рівняння ББГКІ.

Зіткнення між частинками призводить до зміни їхніх швидкостей. Якщо задає імовірність розсіювання частинки із стану зі швидкістю у стан зі швидкістю , то інтеграл зіткнень для класичних частинок записується у вигляді

.

У випадку квантового характеру статистики частинок цей вираз ускладнюється неможливістю двох частинок перебувати в стані з одинаковими квантовими числами, а тому потрібно враховувати неможливість розсіювання в зайняті стани.

Рівняння Больцмана - складне інтегродиференціальне рівняння в часткових похідних. Окрім того, інтеграл зіткнень залежить від контретної системи, від типу взаємодії між частинками та інших факторів. Знаходження загальних характеристик нерівноважних процесів - непроста справа.

Однак, відомо, що в стані термодинамічної рівноваги інтеграл зіткнень дорівнює нулю. Справді, в стані рівноваги в однорідній системі при відсутності зовнішніх полів усі похідні в лівій частині рівняння Больцмана дорівнюють нулю, тож інтеграл зіткнень теж повинен дорівнювати нулю.

При малих відхиленнях від рівноваги функцію розподілу можна подати у вигляді

,

де - рівноважна функція розподілу, що залежить лише від швидкостей частинок і відома з термодинаміки, а f₁ - невелике відхилення.

В цьому випадку можна розкласти інтеграл зіткнень у ряд Тейлора відносно функції f₁, і записати його у вигляді:

,

де τ - час релаксації. Таке наближення називається наближенням часу релаксації.

Час релаксації, який входить у рівняння Больцмана залежить від швидкості частинок, а отже енергії. Час релаксації можна розрахувати для конкретної системи із конкретним процесами розсіювання частинок.

Рівнянн Больцмана в наближенні часу релаксації записується у вигляді

.

Рівняння Больцмана застосовують для опису плазми, в теорії твердого тіла тощо, всюди, де вивчаються транспортні явища: електропровідність, термоелектричні явища, дифузія, ефект Хола та ін.