Лекция №1
Вспуплении. Краткая историческая справка.
Информационные основи функционирования СОИ
Логические основы функционирования СОИ
При описании эволюции ВТ обычно используют один из двух подходов: хронологический или технологический. В первом случае — это хронология событий, существенно повлиявших на становление ВТ. Для наших целей больший интерес представляет технологический подход, когда развитие вычислительной техники рассматривается в терминах архитектурных решений и технологий. По словам главного конструктора фирмы DEC и одного из изобретателей мини-ЭВМ Белла: — «История компьютерной индустрии почти всегда двигалась технологией».
В качестве узловых моментов, определяющих появление нового поколения ВТ, обычно выбираются революционные идеи или технологические прорывы, кардинально изменяющие дальнейшее развитие средств автоматизации вычислений. Одной из таких идей принято считать концепцию вычислительной машины с хранимой в памяти программой, сформулированную Джоном фон Нейманом. Взяв ее за точку отсчета, историю развития ВТ можно представить в виде трех этапов:
донеймановского периода;
эры вычислительных машин и систем с фон-неймановской архитектурой;
постнеймановской эпохи — эпохи параллельных и распределенных вычислений, где наряду с традиционным подходом все большую роль начинают играть отличные от фон-неймановских принципы организации вычислительного процесса.
Значительно большее распространение, однако, получила привязка поколений к смене технологий. Принято говорить о «механической» эре (нулевое поколение) и последовавших за ней пяти поколениях ВС [210]. Первые четыре поколения традиционно связывают с элементной базой вычислительных систем: электронные лампы, полупроводниковые приборы, интегральные схемы малой степени интеграции (ИМС), большие (БИС), сверхбольшие (СБИС) и ультрабольшие (УБИС) интегральные микросхемы. Пятое поколение в общепринятой интерпретации ассоциируют не столько с новой элементной базой, сколько с интеллектуальными возможностями ВС. Работы по созданию ВС пятого поколения велись в рамках четырех достаточно независимых программ, осуществлявшихся учеными США, Японии, стран Западной Европы и стран Совета экономической взаимопомощи. Ввиду того, что ни одна из программ не привела к ожидаемым результатам, разговоры о ВС пятого поколения понемногу утихают. Трактовка пятого поколения явно выпадает из «технологического» принципа. С другой стороны, причисление всех ВС на базе сверхбольших интегральных схем (СБИС) к четвертому поколению не отражает принципиальных изменений в архитектуре ВС, произошедших за последние годы. Чтобы в какой-то мере проследить роль таких изменений, воспользуемся несколько отличной трактовкой, предлагаемой в [174]. В работе выделяется шесть поколений ВС. Попытаемся кратко охарактеризовать каждое из них, выделяя наиболее значимые события.
Нулевое поколение (1492–1945)
Для полноты картины упомянем два события, произошедшие до нашей эры: первые счеты — абак, изобретенные в древнем Вавилоне за 3000 лет до н. э., и их более «современный» вариант с косточками на проволоке, появившийся в Китае примерно за 500 лет также донэ
«Механическая» эра (нулевое поколение) в эволюции ВТ связана с механическими, а позже — электромеханическими вычислительными устройствами. Основным элементом механических устройств было зубчатое колесо. Начиная с XX века роль базового элемента переходит к электромеханическому реле. Не умаляя значения многих идей «механической» эры, необходимо отметить, что ни одно из созданных устройств нельзя с полным основанием назвать вычислительной машиной в современном ее понимании. Чтобы подчеркнуть это, вместо термина «вычислительная машина» будем использовать такие слова, как «вычислитель», «калькулятор» и т. п.
Простейшие цифровые вычислительные устройства .
Абак и счеты
Самыми важными арифметическими операциями с точки зре-ния образованного человека древнего мира . купца или сборщиканалогов,. были сложение и вычитание. Труднопредставить себе,как с ними могли бы справиться, скажем, римляне, пользуясьтоль-ко принятой у них непозиционной системой счисления. Попробуй-те, например, решить такую простенькую задачку с римскимицифрами:
MCMXCVI + CCLXIV = ?
К счастью, уже древние римляне располагали простейшим приспособлениемдляускорениясчета, основанным на позиционнойсистеме счисления,который назывался абак. Абак представляет со-бой дощечку, разделеннуювертикальными перегородками на не-сколько отделений, соответствующим отдельным разрядам числа впозиционной системесчисления. Вотделенияхпомещалиськамеш-ки (по латыни«камешек» .«calculus», отсюдапроисхождение слов«калькуляция», «каль-кулятор»). Число их вотделении равно значе-нию разряда и можетменяться (в десятичной Древнеримский абак26
системе счисления) от 0 до 9. Сложение чисел производится путемпоразрядногодобавления камешков, при переполнении отделенияоно очищается и делается перенос единицы в следующий разряд.Вот и все . просто и быстро. Единственное неудобство . камеш-ки легко рассыпаются и могут потеряться припереноске.
Арабские купцы разнесли абак по всемумиру. Практичные китайцы нанизали камеш-
ки на спицы, вставили их в деревянную рамуи повернули все на 90 градусов. В таком виде
абак в XVI веке попал в Россию и стал назы-ваться русскими счетами. Прошло более 400
лет, а счеты на Руси и ныне в ходу. Некото-рые продавцы и официанты любят их боль-
ше, чем электронные калькуляторы, можетбыть, потому, что со счетами легче «ошибить-
ся» в стоимости покупки (в свою, разумеет-ся, пользу).
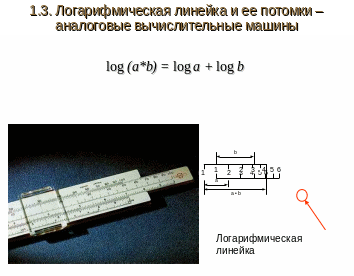
1.3. Логарифмическая линейкаи ее потомки . аналоговыевычислительные машины
Если спросить молодого человека, живущего в конце XX века,
что он думает о науке и технике XVII века, он, скорее всего, высо-
комерно выскажется о «первобытном и примитивном» уровне раз-
вития. И будет абсолютно неправ, так как XVII век . одна из
высочайших вершин человеческого гения. Шекспир и Бах, Ньютон
и Паскаль, Лейбниц и Декарт . все это XVII век. В этом веке были
сделаны великие географические открытия, заложены основы со-
временной физики и математики, сооружены грандиозные здания
вроде собора св. Павла в Лондоне, изобретены телескоп, микро-
скоп, термометр, барометр, придуманы логарифмы и построены
Русские счеты27
первые механические вычислительные машины.
В этом параграфе мы поговорим о логарифмической линейке,
которая появилась в первой трети XVII века, вскоре после того, как
в 1614 году шотландский барон Джон Непер (Nepier, John; 1550-
1617) опубликовал свою первую книгу «Magnifici logarithmorum
cannonis discriptio». Я надеюсь, читатель еще представляет себе ло-
гарифмическую линейку, которая более трех веков верой и прав-
дой служила бесчисленным поколениям ученых и инженеров,
студентов и школьников. Даже когда появились электронные каль-
куляторы, многие инженеры предпочитали пользоваться испытан-
ным и надежным помощником . линейкой. Рассказывают, что автор
проекта останкинской телебашни инженер Н.В.Никитин (кстати,
выпускник Томского политехнического института) все расчеты сде-
лал на логарифмической линейке. Когда об этом узнали руководя-
щие товарищи (дело было в 1960-е годы), они всполошились, работу
остановили, и заставили пере-проверить вычисления на ком-пьютерах. Но все оказалось в
порядке,. и башня, как видим,стоит до сих пор.
Принцип действия лога-рифмической линейки основанна основном правиле логариф-мов:
log(a.b) = log(a) + log(b),
что позволяет заменить опера-1 2 3 4 5 6
1 2 3 4 5 6
a
b
a . b
Принцип действия
логарифмической линейки
a=2, b=3, a.b=6
Логарифмическая линейка
28
цию умножения сложением, а операцию деления . вычитанием.
Само же сложение (вычитание) производится путем простого пре-
мещения двух реек с нанесенными на них одинаковыми логариф-мическими шкалами
Нас, однако, будут интересовать сейчас не конкретные приемы
работы с логарифмической линейкой, а более общий вопрос о вза-
имоотношении дискретного и непрервного в вычислительной тех-нике.
На абаке или счетах число представляется в цифровой, т.е. в
символической,"знаковой форме, и это представление совершенно
точное. Если 375 так 375, не больше и не меньше. Каждый разряд
числа изображается целым числом камешков, нельзя положить 3 с
половиной или 5 и 6 десятых камня. Даже если число не целое, то
точно представляется соответствующая ему десятичная дробь с
фиксированным числом знаков после запятой. Поэтому абак явля-
ется простейшим примером цифровой или, более точно, дискрет-
ной вычислительной машины (так как представляться могут не
только числа, но и другие дискретные объекты).
В противоположность абаку, на логарифмической линейке пред-
ставляется не цифровая запись числа, а некоторый его физический
аналог. Первому сомножителю соответствует перемещение движка
относительно неподвижной шкалы, второму . перемещение визи-
ра бегунка относительно шкалы движка, результату . перемеще-
ние бегунка относительно неподвижной шкалы. Аналоги являются
непрерывными физическими величинами, поэтому представление
всегда не точное, а приближенное, так как невозможно точно выс-
тавить движок на цифру, скажем, 2 . будет или меньше или боль-
ше.. да и сами шкалы имеют некоторую погрешность. Таким
образом, логарифмическая линейка является простейшим приме-
ром аналоговой вычислительной машины.
Цифровые (дискретные) и аналоговые вычисления . это две
постоянно сосуществующие и конкурирующие ветви математики.
Математика древнего мира была в подавляющей степени связана с
аналоговыми (геометрическими) построениями. Строго говоря, цир-
куль и линейка . это тоже древнейшая аналоговая вычислитель-29ная машина.
С изобретением симво-лических алгоритмов ариф-метики роль аналоговых
вычислений стала ослабе-вать, так как цифровые ме-тоды способны обеспечить
более высокую точностьвычислений. Обычная ло-гарифмическая линейка,
например, дает результат сточностью до 1 . 0.1 %(2.3 знаков после запя-той), причем ошибка быст-ро накапливается сувеличением сложностивычислений. Для астрономии или географии, например, такая точ-ность совершенно недостаточна, поэтому, начиная с XVII века, кон-структорская мысль была направлена в основном на создание и
развитие цифровых вычислительных машин, и что из этого полу-чилось . мы увидим дальше.
Однако не всегда и не везде нужна астрономическая точность,поэтому, параллельно с цифровой, развивалась и аналоговая вы-числительная техника. В XIX и XX веках для аналоговых вычисле-ний использовались самые различные физические процесссы:механические1, гидравлические, после изобретения радиоламп и
транзисторов . электронные. Еще в 1960-х годах популярность ана-
1В 1930 г. профессор Массачусетского технологического института (МТИ) Ванне-вар Буш (Boosh, Vannevar; 1890-1974) построил «дифференциальный анализатор»
. большую механическую аналоговую машину, способную решать сложные диф-
ференциальные уравнения. Он представлял собой сложнейшую систему реек, шес-
теренок, валиков размером с целую комнату. Обязанности оператора на этой машине
выполнял молодой аспирант Клод Шеннон (Shannon, Claude; р. 1916 ) . будущий
автор теории информации. С тех пор МТИ стал крупнейшим центром исследований в
области вычислительной техники и информатики.Большая аналоговая
вычислительная машина(1960-е годы).
