Методические рекомендации по решению задач.

Задача 1

Даны векторы и . Найти вектор = + , скалярное произведение ( · ) и модуль вектора , где = (1; 4; -1; -5), = (5; -1; 5; 2).

Решение:

Вектор находится как сумма двух векторов и . Для того чтобы найти сумму двух векторов заданных координатами необходимо сложить их соответствующие координаты.

= + = (1; 4; -1; -5) + (5; -1; 5; 2) = (6; 3; 4; -3).

Скалярное произведение векторов – это число, полученное как сумма произведений соответствующих координат векторов.

· = 1·5 + 4·(-1) + (-1)·5 + (-5)·2 = -14

Длина вектора находится по формуле:

, где = .

Тогда:

Задача 2

Найти значение матрицы D = A · B – C² и вычислить ее определитель, если даны матрицы:

A = , B = , C = .

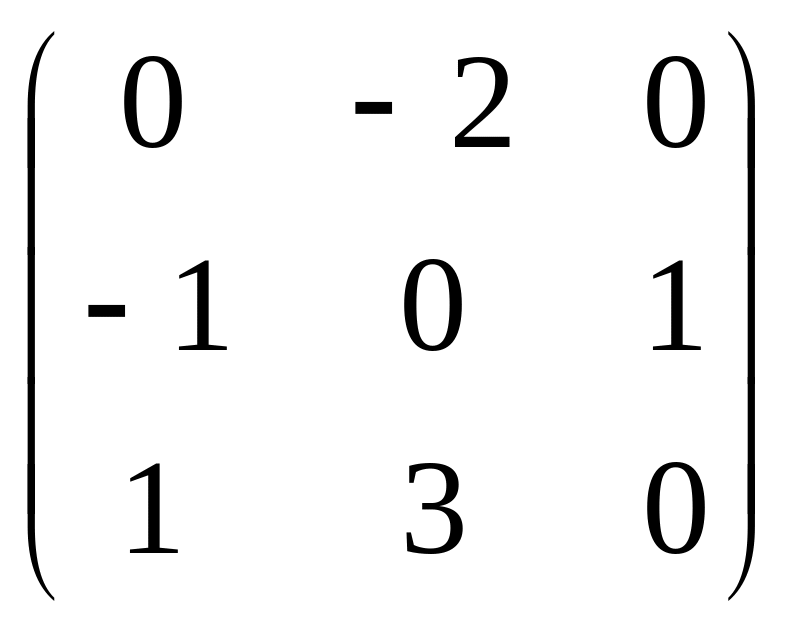Решение:

Для того чтобы найти значение матрицы D, необходимо в первую очередь найти произведение матриц А и В. Операция умножения двух матриц возможна только в случае, если число столбцов первой матрицы равно числу строк второй матрицы, тогда . Произведением матрицы на матрицу называется матрица такая, что , где i = 1,..m; k = 1,...p, то есть элемент i-й строки и k-го столбца матрицы произведения C равен сумме произведений элементов i-й строки матрицы A на соответствующие элементы k-го столбца матрицы B. Тогда произведение двух матриц A и B:

Аналогично находим С² , как произведение матрицы С на саму себя, то есть:

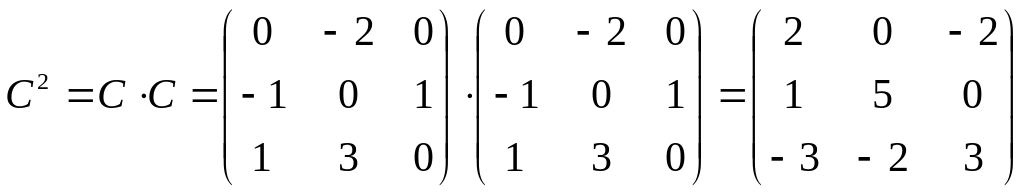
Для того, чтобы найти разность двух матриц необходимо найти разность соответствующих элементов этих матриц:

Вычислим определитель матрицы D разложением по первой строке, так как первая строка содержит больше всего нулей:

Задача 3

Решить систему из трех уравнений

1. по формулам Крамера;

2. методом Гаусса.

Решение:

a) При решении системы с использованием формул Крамера необходимо составить определители. Обозначим ∆ - главный определитель системы (составляется из коэффициентов при переменных), а ∆_i - дополнительные определители (составляются из главного путем замены i-того столбца коэффициентов на столбец свободных членов). Формулы: , где i = 1,...n называются формулами Крамера.

Составим определители и вычислим их:

18, 54, 36, 18. Значит, , , .

b) Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе система приводится к ступенчатому виду с помощью элементарных преобразований расширенной матрицы системы. На втором этапе идет последовательное определение неизвестных из полученной ступенчатой системы.

Для решения данной системы уравнений составим расширенную матрицу системы из коэффициентов при переменных и столбца свободных членов. С помощью элементарных преобразований приведем ее к ступенчатому виду:

В результате исходная система преобразовалась к ступенчатой (восстановим запись системы из полученной ступенчатой матрицы ):

Решение данной системы: x = 3, y = 2, z = 1.

Задача 4

a) Найти точку пересечения прямых и

b) Найти уравнение прямой, проходящей через точку (1; 2) перпендикулярно к прямой

c) Найти уравнение прямой, параллельной к прямой и проходящей через точку (2; 1)

d) Какая кривая описывается уравнением ? Написать каноническое уравнение этой кривой.

Решение:

a) Задача о нахождении точки пересечения двух прямых сводится к отысканию точки, координаты которой являются решением системы двух уравнений с двумя неизвестными:

Таким образом точка пересечения имеет координаты:

3. Уравнение прямой, проходящей через точку (x₀; y₀) имеет вид:

y –y₀ = k (x – x₀).

Для нахождения углового коэффициента k воспользуемся условием перпендикулярности двух прямых: . Тогда искомое уравнение прямой: , где угловой коэффициент прямой: . Запишем полученное уравнение прямой в общем виде: или x - 2y + 3 = 0.

c) В данной задаче воспользуемся условием параллельности двух прямых: k₁ = k₂. Тогда уравнение искомой прямой: , где угловой коэффициент прямой: k₁ = k₂ =2. Запишем полученное уравнение прямой в общем виде: 2x – y – 3 = 0.

d) Данная кривая является эллипсом. Каноническое уравнение эллипса: . Приведем уравнение к каноническому виду: . Тогда: .

Задача 5

Найти производные функций:

а) y = 2x^-3/2

b) y = x²·cos (5x+1) +

c) y = ln(sin(5x+1))

Решение:

Для нахождения производных функций необходимо воспользоваться таблицей производных и правилами дифференцирования.

а) Найдем производную функции y = 2x^-3/2 . Для этого вынесем постоянный множитель за знак производной и воспользуемся формулой из таблицы производных: . Получим:

b) Найдем производную функции y = x²·cos (5x+1) + . Для этого воспользуемся правилами дифференцирования: ; ; и формулами из таблицы производных: , . Функция cos(5x+1) является сложной функцией, где cos(5x+1) = cos(u), u = 5x+1. Тогда по правилу дифференцирования сложной функции . Аналогично находится производная функций cos(3x) и ln(4x). Получим: =

c) Найдем производную функции y = ln(sin(5x+1)). Данная функция является сложной, где y = ln(z), z = sin(u), u = 5x+1. По правилу дифференцирования сложной функции получим . Тогда:

Задача 6

Найти вторую производную функции: у = .

Решение:

По определению: .

Найдем производную первого порядка используя правила дифференцирования и формулу . Получим:

= .

Тогда: = = = .

Задача 7

Разложить по формуле Тейлора в окрестности точки х = 0 до членов порядка х² функцию и найти ее приближенное значение при х = 0,1.

Решение:

Формула Тейлора в окрестности точки х = 0 имеет вид:

,

где n! = 1·2·3·4·….·n.

Для того, чтобы разложить заданную функцию до членов порядка х², необходимо найти , , . Найдем: ; . Тогда: , , . Получим следующее разложение: . Найдем приближенное значение функции при х = 0,1:

Задача 8

Исследовать функцию и построить ее график:

Решение:

Исследовать функцию и построить ее график:

Решение:

Схема исследования функции:

1. Область определения функции, точки разрыва.

2. Интервалы возрастания и убывания функции.

3. Найти точки экстремума.

4. Интервалы выпуклости и вогнутости функции.

5. Найти точки перегиба.

6. Асимптоты графика функции.

На основании проведенного исследования строится график функции.

Область определения функции – вся числовая ось, то есть . Значит, точек разрыва нет.

Найдем интервалы монотонности и экстремумы функции, исследуя первую производную: . Производная обращается в нуль при х = 0. При х < 0 производная положительная, а при x > 0 производная отрицательная. Это означает, что функция возрастает на и убывает на . В точке х = 0 функция имеет максимум.

Чтобы определить интервалы выпуклости и точки перегиба, вычислим вторую производную функции: . Вторая производная обращается в нуль при . Тогда и . Вторая производная положительна на интервалах: , следовательно на этих интервалах функция вогнута. Вторая производная отрицательна на , тогда функция на этом интервале выпукла. Точки и - это точки перегиба функции.

Найдем асимптоты графика функции. Вертикальных асимптот нет, так как область определения . Найдем наклонную асимптоту . Для этого найдем предел: . Следовательно, наклонной асимптоты нет. Горизонтальная асимптота , где . Тогда y = 0.

Для построения графика вычислим значения функции в найденных точках: , .

Построим график функции:

Задача 9

Найти неопределенные интегралы:

1. ;

2. ;

c) ;

d)

Решение:

a) Для нахождения интеграла можно использовать свойства интегралов: интеграл от разности функций равен разности интегралов; постоянный множитель можно вынести за знак интеграла, а также формулу .

.

b) Данный интеграл не является табличным, поэтому для его нахождения можно применить замену переменной. Заменим 1+2x² на t, то есть t = 1+2x² . Тогда по правилу вычисления дифференциала , следовательно .

=

3. При вычислении интеграла от дробно-рациональной функции вида можно в знаменателе подынтегральной функции выделить полный квадрат и сделать замену переменной.

Например, для преобразуем знаменатель подынтегральной функции . Сделаем замену переменной t = x-2. Тогда х = t+2, dx = dt.

.

Получили сумму из двух интегралов. Второй интеграл табличный , где а = 1, а в первом интеграле сделаем замену переменной u = t² – 1, тогда tdt = du/2.

d) Данный интеграл находится методом интегрирования по частям:

.

Пусть . Тогда по формуле интегрирования по частям:

Задача 10

Найти определенные интегралы:

a) ;

b) ;

с) найти площадь фигуры ограниченной кривой и осью абсцисс.

Решение:

a) Для вычисления интеграла используем метод непосредственного интегрирования. В результате получим:

b) Для вычисления данного интеграла воспользуемся методом замены переменной. Пусть t = sin(2x), тогда dt = (sin2x)´dx = 2·cos(2x)dx. Следовательно cos(2x)dx = dt/2. Также необходимо заменить пределы интегрирования, так как произошла замена исходной переменной:

.

с) Площадь фигуры, ограниченной сверху кривой y = f(x), снизу осью OХ, слева прямой x = a и справа прямой y = b можно вычислить по формуле Ньютона–Лейбница: , где F(x) – первообразная для функции f(x).

Фигура ограничена сверху графиком кривой , снизу осью ОХ. Эта площадь находится как интеграл от функции f(x), а пределы интегрирования – координаты точек пересечения параболы с осью OX. Найдем эти точки, решив уравнение . Корнями данного уравнения являются числа: и . Поэтому нижний предел интегрирования равен 0, а верхний равен 2. Тогда:

Задача 11

Найти первые частные производные функций.

a) ;

b) .

Решение:

Частные производные функции двух и более переменных определяется по тем же формулам и правилам, что и функция от одной переменной. Следует помнить одно правило: если по одной переменной дифференцируем функцию, то остальные переменные считаются постоянными в этой функции.

a) Имеем функцию от двух переменных х и у: . Тогда частные производные:

,

b) Данная функция является функцией от трех переменных x, y, z: . Тогда частные производные:

;

;

.

Задача 12

Найти градиент функции z(x;y) в точке (х_о, у_о), если z= cos(2x + 11y), x₀ = y₀ = π/2

Решение:

Градиентом функции z(x;y) называется вектор с координатами (z´_x , z´_y ).

Имеем: , . Найдем значения частных производных в точке x₀ = y₀ = π/2:

Градиент функции z в точке (π/2; π/2):

Задача 13

Исследовать на экстремум функцию z = х² - ху + (у + 1)² .

Решение:

Найдем первые частные производные функции: ; . Точки, в которых частные производные не существуют, отсутствуют. Найдем критическую точку, решая систему уравнений: . Отсюда получаем точку М(-2/3; -4/3). Найдем частные производные второго порядка данной функции: , , . Найдем значение > 0, при этом > 0. Следовательно функция имеет минимум в точке М(-2/3; -4/3).

Задача 14

Найти общее решение дифференциальных уравнений и проверить правильность найденных решений дифференцированием:

a) ;

b) .

Решение:

Данное дифференциальное уравнение относится к виду , допускающему понижение порядка до тех пор, пока не получим решение уравнения. Для этого необходимо проинтегрировать правую и левую часть уравнения. Полученное уравнение имеет порядок на единицу ниже, чем исходное, то есть: .

a) Решим дифференциальное уравнение первого порядка . Получим:

.

Для того чтобы проверить правильность найденного решения, необходимо найти производную найденной функции: . Получим исходное дифференциальное уравнение. Следовательно найденное решение верно.

b) Решим дифференциальное уравнение второго порядка с помощью двукратного интегрирования . Тогда: , .

Проверим правильность найденного решения. Для этого найдем первую и вторую производную найденной функции. , .

Получим исходное дифференциальное уравнение. Следовательно найденное решение верно.

Задача 15

Найти решения дифференциальных уравнений с разделяющимися переменными :

a)

b)

Решение:

Уравнения вида: называется дифференциальным уравнением первого порядка с разделяющими переменными. В нем одно слагаемое зависит только от х, а другое – от у. Проинтегрировав почленно это уравнение, получаем: - это общий интеграл.

a) Разделим обе части уравнения на : . Проинтегрируем обе части уравнения и получим: (произвольную постоянную здесь удобно записать именно так), где С > 0. Тогда - общий интеграл исходного уравнения. При делении на мы могли потерять решение y = -1 и x = 1. Так как С > 0, то оно не содержится в общем интеграле. Таким образом данное уравнение имеет особые решения: y = -1 и x = 1.

b) Уравнение вида также сводится к уравнению с разделяющимися переменными.

Решим уравнение: . Поскольку , то . Разделим переменные: . Проинтегрировав обе части уравнения получим: . Выразим у: . Это общее решение дифференциального уравнения.

При разделении переменных произошло деление на , поэтому мы могли потерять решение y = 0. Оно не содержится в общем решении. Таким образом данное уравнение имеет особое решение y = 0.

Задача 16

Найти решение линейного однородного уравнения с постоянными коэффициентами: у" -2у' + 10у = 0 с условиями у = 0, у' = 1 при х = 0.

Решение:

Уравнения вида , где p и q постоянные, называется линейным однородным дифференциальным уравнением с постоянными коэффициентами. Для решения необходимо составить характеристическое уравнение , заменив на соответственно. При решении характеристического уравнения возможны следующие три случая:

1. корни уравнения k₁ , k₂ - действительные и различные, тогда общее решение дифференциального уравнения имеет вид:

2. корни уравнения k₁ , k₂ - действительные и равные, тогда общее решение дифференциального уравнения имеет вид:

3. корни уравнения k₁ , k₂ - комплексно-сопряженные, то есть , тогда общее решение дифференциального уравнения имеет вид:

Решим уравнение . Составим характеристическое уравнение: . Корни уравнения . В этом случае общее решение уравнения имеет вид: .

.

Подставляя начальные условия у = 0, у' = 1 при х = 0 в полученное общее решение и его производную, получаем систему уравнений относительно С₁ и С₂ :

Найденные константы подставляем в общее решение. Получаем искомое частное решение уравнения, удовлетворяющее начальным условиям:

Задача 17

Найти решение линейного неоднородного уравнения с постоянными коэффициентами в виде суммы общего решения однородного уравнения и произвольного частного решения неоднородного уравнения:

у" - 2 у' + у = 5.

Решение:

Общее решение данного уравнения представим в виде: , где - общее решение однородного уравнения, а - частное решение неоднородного уравнения.

Найдем общее решение однородного уравнения . При решении характеристического уравнения получим корни . Тогда

Частное решение для линейного уравнения, в правой части которого стоит константа, ищется в виде , где А – константа. Подставив это решение в исходное уравнение и учитывая что производная от константы равна нулю, получим А = 5, следовательно .

Общее решение неоднородного уравнения .