Тема Интегральное исчисление функции одной переменной. Неопределенный интеграл.

Функция F(x) называется первообразной для функции f(x) на интервале (a, b), если для всех x из этого интервала выполняется равенство

(34)

Неопределенным интегралом от функции f(x) называется множество всех первообразных функции , и обозначается .

Операция интегрирования является обратной к операции дифференцирования.

Таблица 4.

Таблица интегралов

1.	9.
2.	10.
3.	11.
4.	12.
5.	13.
6.	14.
7.	15.
8.	16.

Основные свойства неопределенного интеграла.

1. 

2. 

3. 

4. 

Основные методы интегрирования

1. Метод непосредственного интегрирования.

2. Метод замены переменной (метод подстановки) заключается во введении новой переменной интегрирования. При этом заданный интеграл сводится к новому, который является табличным.

(35)

3. Интегрирование по частям.

(36)

Выделяют два типа интегралов, берущихся по частям:

1. ; ; ;

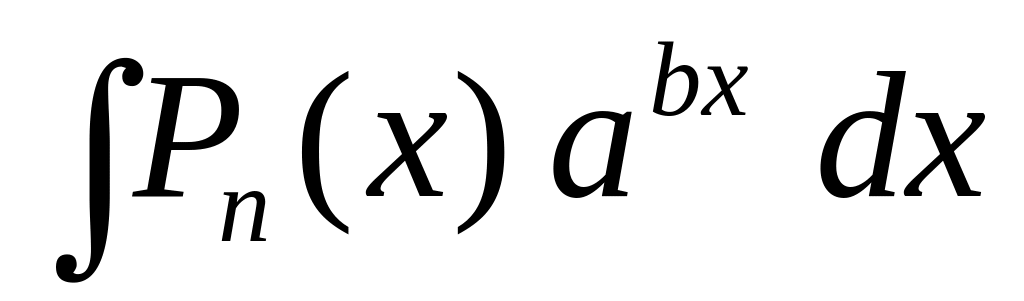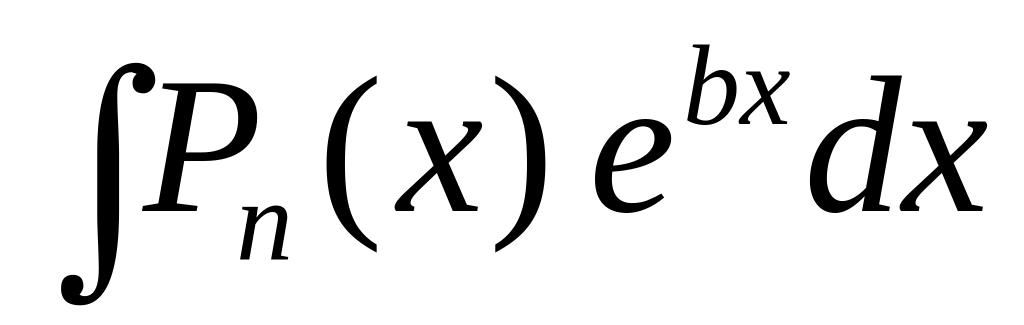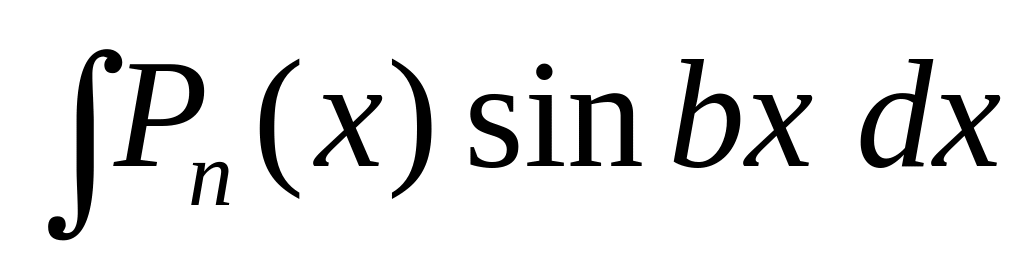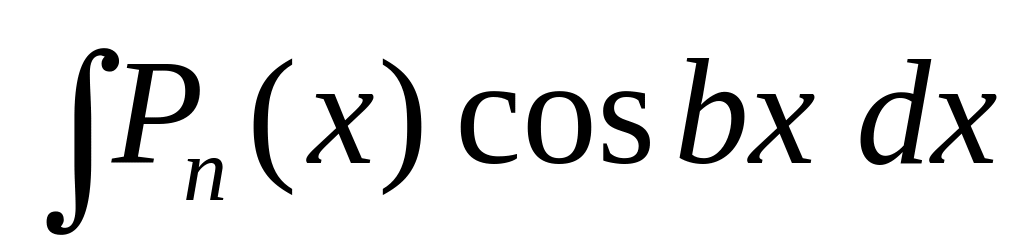
Здесь за u принимают многочлен , а за – остальные сомножители.

2. ; ; ;

Здесь за принимают , а за u – остальные сомножители.

4. Интегрирование рациональных дробей

Рациональной дробью называется функция, равная отношению двух многочленов, т.е. . Для интегрирования рациональной дроби необходимо представить ее в виде суммы простейших дробей видов:

,

где k, – целое положительное число, а трехчлен не имеет действительных корней.

Если дробь неправильная, то необходимо выделить целую часть дроби.

5. Интегрирование некоторых тригонометрических функций

Для нахождения интегралов типа используют:

1. формулы понижения степени:

, (37)

2. подстановку 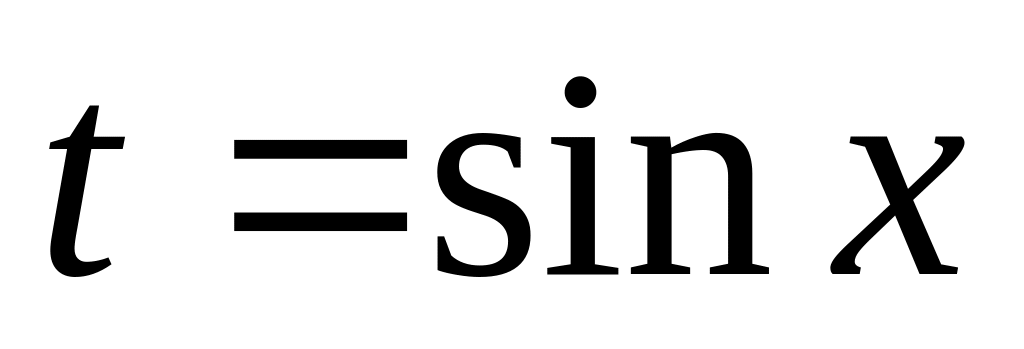, если n – нечетное;

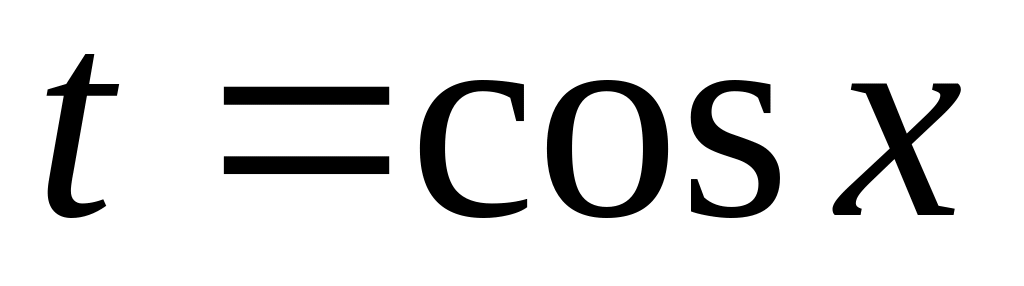3. подстановку , если m – нечетное/

Для нахождения интегралов вида , где R – рациональная функция, используют универсальную подстановку: , при этом.

, (38)

Тема Интегральное исчисление функции одной переменной. Определенный интеграл.

1. Формула Ньютона–Лейбница

Если функция непрерывна на и , то имеет место формула:

, (39)

2. Несобственные интегралы первого и второго рода

Несобственные интегралы первого рода:

,

Несобственные интегралы второго рода:

, где a – точка бесконечного разрыва функции , и

, где b – точка бесконечного разрыва функции .

Несобственный интеграл называется сходящимся, если существует конечный предел в правой части равенства. Если же предел не существует или равен бесконечности, то интеграл называется расходящимся.

3. Вычисление площади фигуры

Криволинейной трапецией в называется фигура, ограниченная прямыми x = a, x= b, y = 0 и кривой .

Формула для вычисления площади криволинейной трапеции:

(40)

4. Вычисление объема тела вращения

Пусть криволинейная трапеция, ограниченная прямыми x = a, x= b, y = 0 и кривой вращается вокруг оси ОX. Объем полученного при этом тела вращения вычисляется по формуле:

(41)