
- •Оглавление
- •Общие организационно-методические указания
- •Тематический план
- •Рекомендуемая литература
- •Содержание и методические указания к изучению тем дисциплины
- •1 Семестр
- •2 Семестр
- •Справочный материал Тема Векторы в прямоугольной системе координат.
- •Тема Линейная алгебра: матрицы и действия над нами.
- •Тема Линейная алгебра: определители.
- •Тема Линейная алгебра: решение систем линейных уравнений.
- •Методы решения систем линейных уравнений.
- •Формулы Крамера
- •При помощи обратной матрицы.
- •Метод Гаусса.
- •Тема Аналитическая геометрия
- •Кривые второго порядка: эллипс, гипербола, парабола
- •Виды уравнений параболы
- •Тема Функция. Предел и непрерывность функции.
- •Основные эквивалентности (при )
- •Непрерывность функции, точки разрыва
- •Тема Дифференциальное исчисление функции одной переменной
- •Основные правила дифференцирования
- •Правило Лопиталя
- •Исследование функций и построение графиков
- •Тема Интегральное исчисление функции одной переменной. Неопределенный интеграл.
- •Основные свойства неопределенного интеграла.
- •Основные методы интегрирования
- •Тема Интегральное исчисление функции одной переменной. Определенный интеграл.
- •Тема Функции многих переменных
- •Производные фнп высших порядков
- •Экстремумы фнп
- •Тема Дифференциальные уравнения
- •Уравнения с разделяющимися переменными.
- •Линейные дифференциальные уравнения 1-го порядка.
- •Уравнение Бернулли.
- •Однородные уравнения.
- •Дифференциальные уравнения 2-го порядка
- •Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.
- •Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.
- •Тема Ряды
- •Вопросы к экзамену по дисциплине «Математика», 1 семестр
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №3
- •Контрольная работа №4
Основные правила дифференцирования
Производная постоянной равна нулю:
![]() (27)
(27)
Производная алгебраической суммы двух дифференцируемых функций
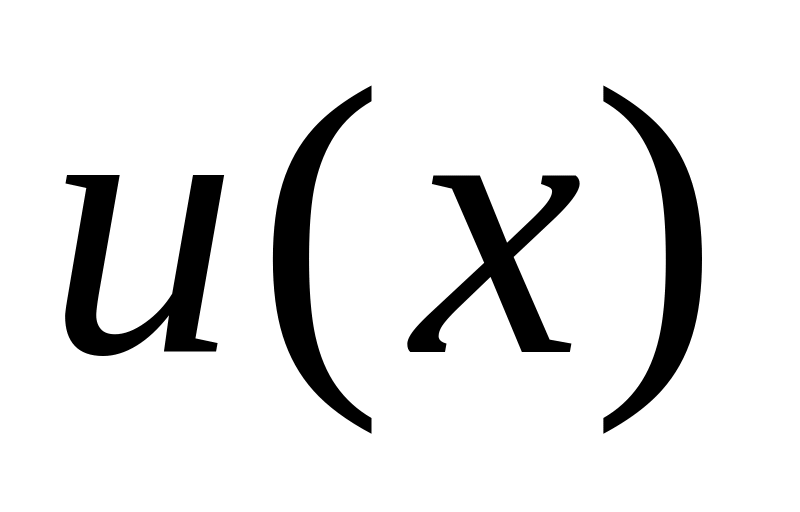 и
и
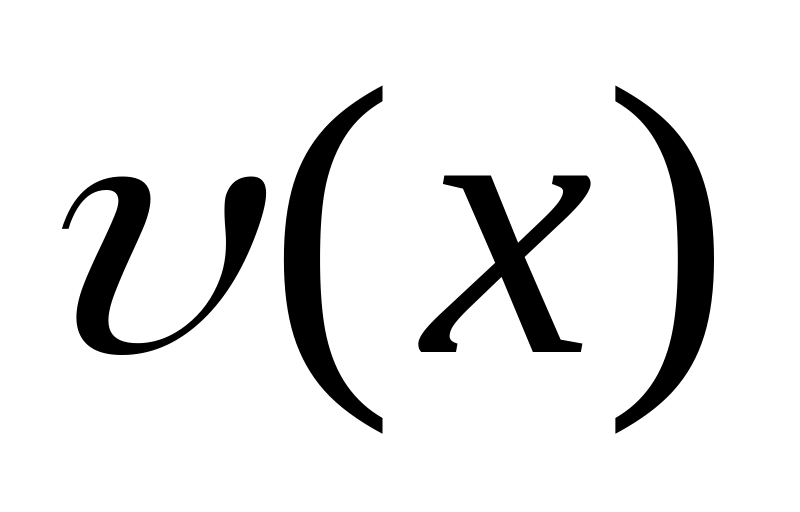 :
:
![]() (28)
(28)
Производная произведения двух дифференцируемых функций и :
![]() (29)
(29)
Производная частного двух дифференцируемых функций и :
![]() (30)
(30)
Постоянный множитель можно выносить за знак производной:
![]() (31)
(31)
Производная сложной функции: если
 ,
где
,
где
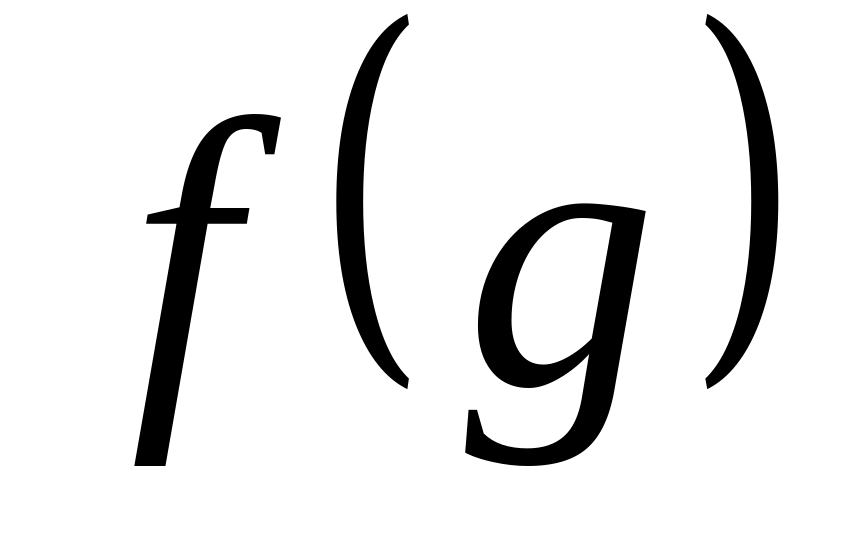 и
и
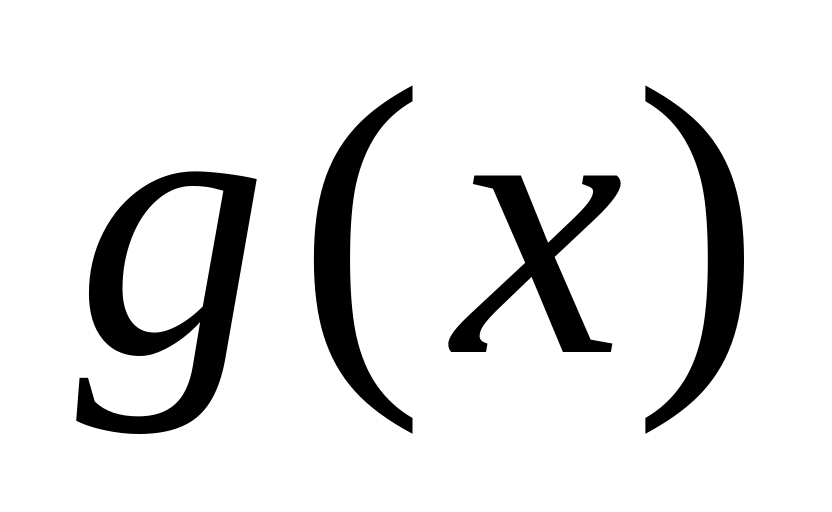 –
дифференцируемые
функции, то
–
дифференцируемые
функции, то
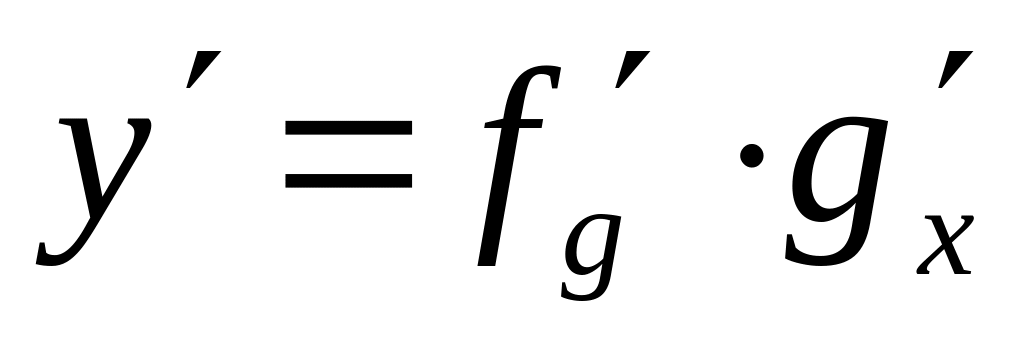 .
.Производные высших порядков: производная 2-го порядка:
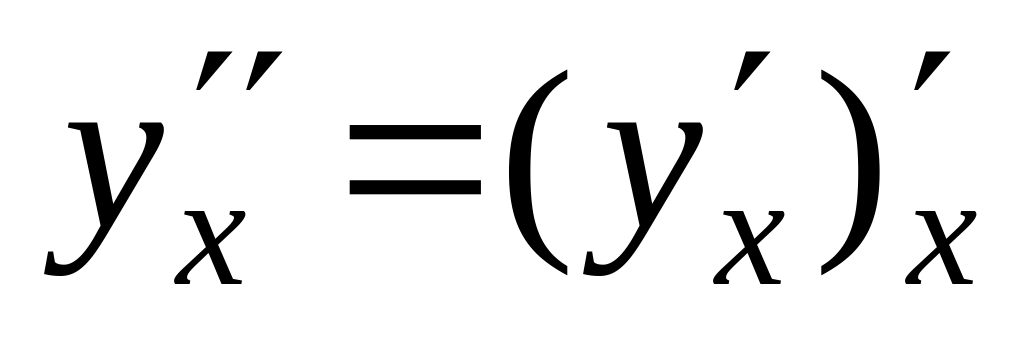 ,
3-го порядка:
,
3-го порядка:
 и т.д. Производная n-го
порядка
и т.д. Производная n-го
порядка
 получается
n-кратным
дифференцированием функции
:
получается
n-кратным
дифференцированием функции
:
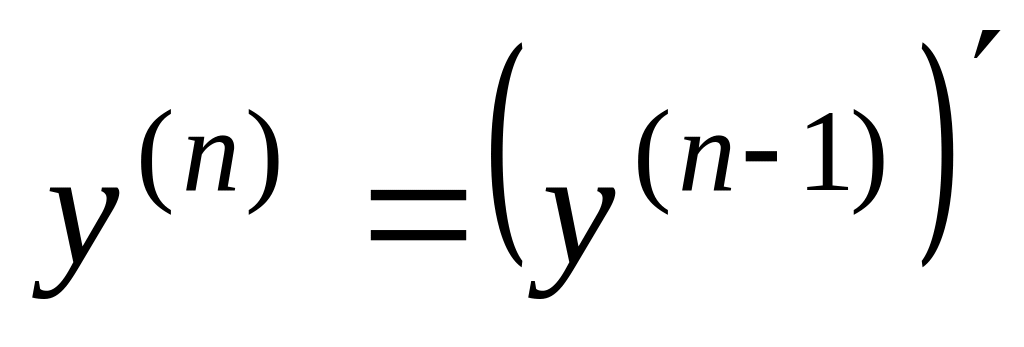 .
.
Правило Лопиталя
Правило Лопиталя: предел отношения двух бесконечно малых или бесконечно больших функций при равен пределу отношения их производных, если предел отношения производных существует:
![]() (32)
(32)
Исследование функций и построение графиков
Исследование функций и построение ее графика производится по следующему плану:
Область определения функции
Четность функции, ее периодичность.
Точки разрыва функции
Промежутки возрастания и убывания функции, экстремумы.
Для определения промежутков монотонности функции используют достаточный признак монотонности.
Достаточный признак монотонности дифференцируемой функции:
если
на интервале
![]() производная
производная
![]() сохраняет знак, то при
сохраняет знак, то при
![]() функция
возрастает, а при
функция
возрастает, а при
![]() ,
то функция
убывает.
,
то функция
убывает.
Для
установления точек экстремумов функции
![]() используют
необходимый и достаточные признаки
существования экстремума.
используют
необходимый и достаточные признаки
существования экстремума.
Необходимое условие существования экстремума функции: если непрерывная функция имеет экстремум в точке , то ее производная в этой точке равна нулю или не существует.
Точки,
принадлежащие
![]() ,
в которых производная
,
в которых производная
![]() равна нулю или не существует, называют
критическими точками функции по ее
первой производной (точками,
«подозрительными на экстремум»).
равна нулю или не существует, называют
критическими точками функции по ее
первой производной (точками,
«подозрительными на экстремум»).
Первый достаточный признак существования экстремума: если при переходе через критическую точку производная изменяет свой знак с плюса на минус, то точка есть точка максимума, если изменяет свой знак с минуса на плюс, то точка есть точка минимума.
Второй
достаточный признак существования
экстремума:
если
![]() – дважды дифференцируемая функция в
точке
и
– дважды дифференцируемая функция в
точке
и
![]() ,
тогда: если
,
тогда: если
![]() ,
то
– точка минимума функции, а если
,
то
– точка минимума функции, а если
![]() ,
то
– точка максимума.
,
то
– точка максимума.
Промежутки выпуклости, вогнутости графика и точки перегиба.
График
функции
называется выпуклым вниз (вогнутым) на
интервале
![]() ,
если он расположен выше любой ее
касательной на этом интервале. График
функции
называется выпуклым вверх (выпуклым)
на интервале
,
если он расположен ниже любой ее
касательной на этом интервале.
,
если он расположен выше любой ее
касательной на этом интервале. График
функции
называется выпуклым вверх (выпуклым)
на интервале
,
если он расположен ниже любой ее
касательной на этом интервале.
Точки графика, отделяющие участки выпуклости от участков вогнутости, называются точками перегиба.
Достаточное
условие выпуклости и вогнутости графика
функции: если
функция
является дважды дифференцируемой и ее
вторая производная
![]() <0
, то график функции на этом интервале
выпуклый вверх. Если
>0
– график выпуклый вниз (вогнутый).
<0
, то график функции на этом интервале
выпуклый вверх. Если
>0
– график выпуклый вниз (вогнутый).
Точки, принадлежащие
графику функции
,
в которых
![]() или не существует, называются критическими
точками функции по ее второй производной
(точками,
«подозрительными на перегиб»).
или не существует, называются критическими
точками функции по ее второй производной
(точками,
«подозрительными на перегиб»).
Достаточное
условие для точек перегиба:
если вторая
производная
![]() при переходе через точку
,
подозрительную на перегиб, меняет знак,
то точка с абсциссой х0
является точкой перегиба.
при переходе через точку
,
подозрительную на перегиб, меняет знак,
то точка с абсциссой х0
является точкой перегиба.
Асимптоты.
а) вертикальные
Прямая
является вертикальной асимптотой
графика функции
,
если функция имеет бесконечный разрыв
в точке
![]() .
Необходимо вычислить односторонние
пределы функции в точках, ограничивающих
промежутки ее
.
.
Необходимо вычислить односторонние
пределы функции в точках, ограничивающих
промежутки ее
.
б) наклонные
Если
график функции
имеет наклонную асимптоту, то ее уравнение
будем искать в виде
![]() .
Параметры k и b можно найти по формулам:
.
Параметры k и b можно найти по формулам:
![]() ,
,
![]() (33)
(33)
Если хотя бы один из этих пределов является бесконечным или не существует, то наклонных асимптот нет. В случае, когда k = 0, график имеет горизонтальную асимптоту с уравнением y = b.
Дополнительные точки графика.
График.
