
- •Оглавление
- •Общие организационно-методические указания
- •Тематический план
- •Рекомендуемая литература
- •Содержание и методические указания к изучению тем дисциплины
- •1 Семестр
- •2 Семестр
- •Справочный материал Тема Векторы в прямоугольной системе координат.
- •Тема Линейная алгебра: матрицы и действия над нами.
- •Тема Линейная алгебра: определители.
- •Тема Линейная алгебра: решение систем линейных уравнений.
- •Методы решения систем линейных уравнений.
- •Формулы Крамера
- •При помощи обратной матрицы.
- •Метод Гаусса.
- •Тема Аналитическая геометрия
- •Кривые второго порядка: эллипс, гипербола, парабола
- •Виды уравнений параболы
- •Тема Функция. Предел и непрерывность функции.
- •Основные эквивалентности (при )
- •Непрерывность функции, точки разрыва
- •Тема Дифференциальное исчисление функции одной переменной
- •Основные правила дифференцирования
- •Правило Лопиталя
- •Исследование функций и построение графиков
- •Тема Интегральное исчисление функции одной переменной. Неопределенный интеграл.
- •Основные свойства неопределенного интеграла.
- •Основные методы интегрирования
- •Тема Интегральное исчисление функции одной переменной. Определенный интеграл.
- •Тема Функции многих переменных
- •Производные фнп высших порядков
- •Экстремумы фнп
- •Тема Дифференциальные уравнения
- •Уравнения с разделяющимися переменными.
- •Линейные дифференциальные уравнения 1-го порядка.
- •Уравнение Бернулли.
- •Однородные уравнения.
- •Дифференциальные уравнения 2-го порядка
- •Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.
- •Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.
- •Тема Ряды
- •Вопросы к экзамену по дисциплине «Математика», 1 семестр
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №3
- •Контрольная работа №4
Основные эквивалентности (при )
|
|
|
Функция
![]() называется бесконечно большой при
называется бесконечно большой при
![]() ,
если
,
если
![]()
Основные теоремы о конечных пределах.
Если = С (С – константа) при
 ,
то
,
то
![]() .
.
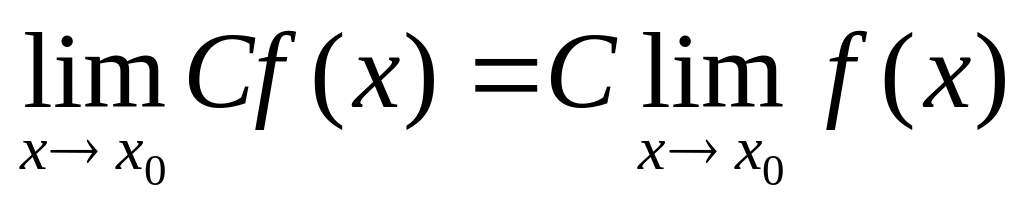
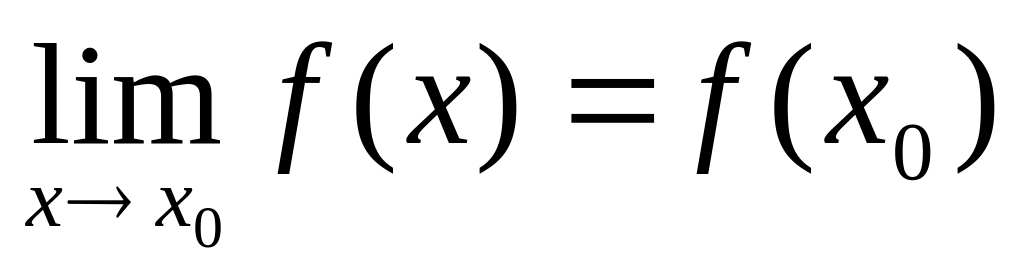 ,
если
–
функция, непрерывная в точке
,
если
–
функция, непрерывная в точке
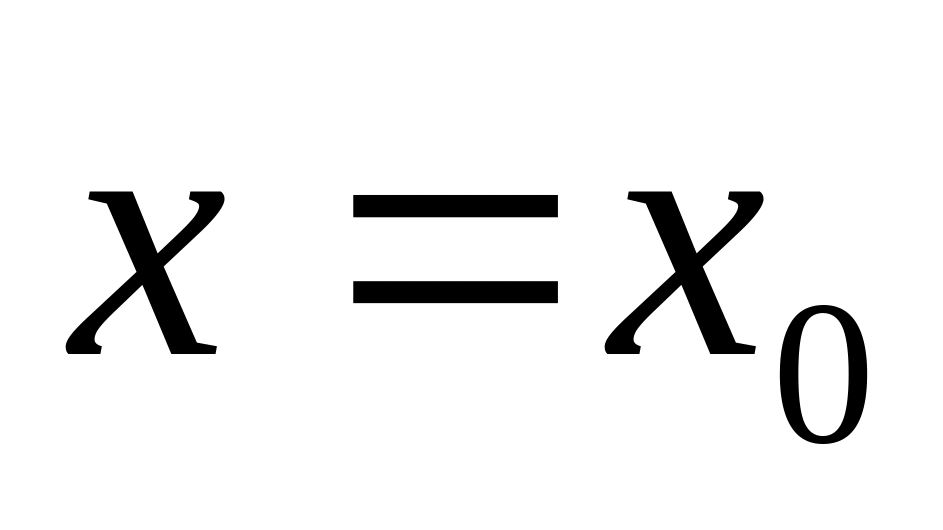 .
.Если
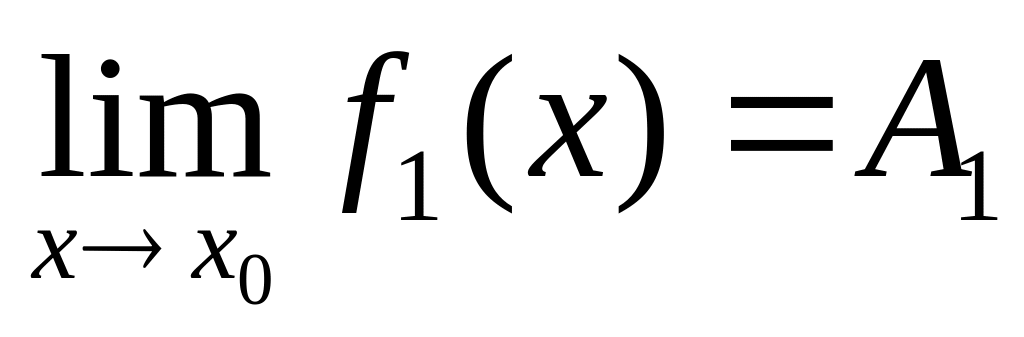 и
и
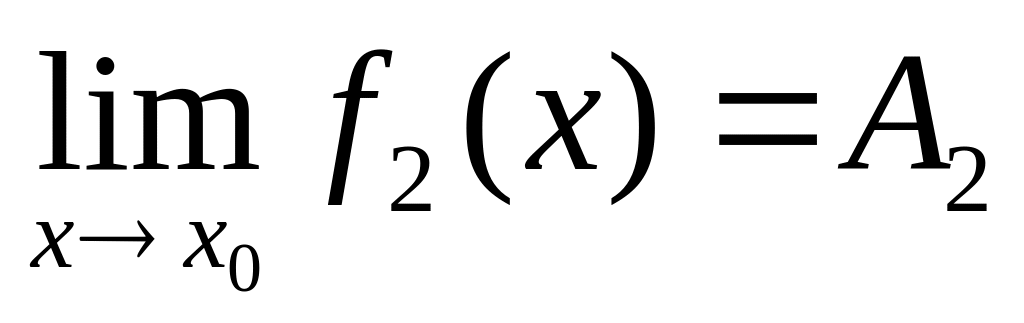 ,
то
,
то
![]()
![]()
![]()
Раскрытие неопределенностей
Чтобы вычислить
предел, имеющий неопределенность, нужно
предварительно преобразовать функцию,
стоящую под знаком предела так, чтобы
неопределенность исчезла, т.е. раскрыть
неопределенность. Основные виды
неопределенностей:
![]() .
.
Правило
1.
Чтобы раскрыть неопределенность
![]() при
при
![]() ,
образованную
,
образованную
отношением двух функций, нужно выражения в числителе и знаменателе почленно поделить на х в старшей степени.
Правило
2.
Чтобы раскрыть неопределенность
![]() при
(где
– число),
образованную отношением двух функций,
нужно в
числителе и знаменателе дроби выделить
критический множитель (х
–
),
и сократить на него дробь.
при
(где
– число),
образованную отношением двух функций,
нужно в
числителе и знаменателе дроби выделить
критический множитель (х
–
),
и сократить на него дробь.
Для выделения критического множителя в случае, когда данная неопределенность образована отношением тригонометрических, показательных, или логарифмических функций, используют замену бесконечно малых функций на их эквивалентности (см. таблицу 2).
Правило
3.
Чтобы раскрыть неопределенность
![]() ,
нужно свести ее ко второму замечательному
пределу:
,
нужно свести ее ко второму замечательному
пределу:
![]() или
или
![]() .
.
Непрерывность функции, точки разрыва
Функция называется непрерывной в точке , если:
1) функция определена в некоторой окрестности точки ;
2)
существует конечный предел ![]()
3) этот предел совпадает со значением функции в точке , т.е.
![]() (25)
(25)
Если функция не является непрерывной в точке , но она определена в окрестности этой точки (за исключением, быть может, самой точки ), то называется точкой разрыва функции.
Для
определения типа разрыва в точке
находят
односторонние пределы
![]() и
и
![]() .
При этом, если оба односторонних предела
конечны в точке
,
то эта точка называется точкой
разрыва первого рода.
Если по-крайней мере один из односторонних
пределов не существует или равен
бесконечности, то точка
называется точкой
разрыва второго рода.
.
При этом, если оба односторонних предела
конечны в точке
,
то эта точка называется точкой
разрыва первого рода.
Если по-крайней мере один из односторонних
пределов не существует или равен
бесконечности, то точка
называется точкой
разрыва второго рода.
Тема Дифференциальное исчисление функции одной переменной
Производной функции в точке х называется конечный предел отношения приращения функции к приращению аргумента:
![]() ,
(26)
,
(26)
где
![]() .
.
Другие
обозначения производной:
![]() .
.
Таблица 3.
Таблица производных основных элементарных функций
1 |
|
8 |
|
2 |
|
9 |
|
3 |
|
10 |
|
4 |
|
11 |
|
5 |
|
12 |
|
6 |
|
13 |
|
7 |
|
|
|
