
- •Оглавление
- •Общие организационно-методические указания
- •Тематический план
- •Рекомендуемая литература
- •Содержание и методические указания к изучению тем дисциплины
- •1 Семестр
- •2 Семестр
- •Справочный материал Тема Векторы в прямоугольной системе координат.
- •Тема Линейная алгебра: матрицы и действия над нами.
- •Тема Линейная алгебра: определители.
- •Тема Линейная алгебра: решение систем линейных уравнений.
- •Методы решения систем линейных уравнений.
- •Формулы Крамера
- •При помощи обратной матрицы.
- •Метод Гаусса.
- •Тема Аналитическая геометрия
- •Кривые второго порядка: эллипс, гипербола, парабола
- •Виды уравнений параболы
- •Тема Функция. Предел и непрерывность функции.
- •Основные эквивалентности (при )
- •Непрерывность функции, точки разрыва
- •Тема Дифференциальное исчисление функции одной переменной
- •Основные правила дифференцирования
- •Правило Лопиталя
- •Исследование функций и построение графиков
- •Тема Интегральное исчисление функции одной переменной. Неопределенный интеграл.
- •Основные свойства неопределенного интеграла.
- •Основные методы интегрирования
- •Тема Интегральное исчисление функции одной переменной. Определенный интеграл.
- •Тема Функции многих переменных
- •Производные фнп высших порядков
- •Экстремумы фнп
- •Тема Дифференциальные уравнения
- •Уравнения с разделяющимися переменными.
- •Линейные дифференциальные уравнения 1-го порядка.
- •Уравнение Бернулли.
- •Однородные уравнения.
- •Дифференциальные уравнения 2-го порядка
- •Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.
- •Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.
- •Тема Ряды
- •Вопросы к экзамену по дисциплине «Математика», 1 семестр
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №3
- •Контрольная работа №4
Тема Линейная алгебра: решение систем линейных уравнений.
Система из n линейных уравнений с n неизвестными
![]()
может быть записана в матричном виде AХ = В, где
 – матрица
коэффициентов системы,
– матрица
коэффициентов системы,
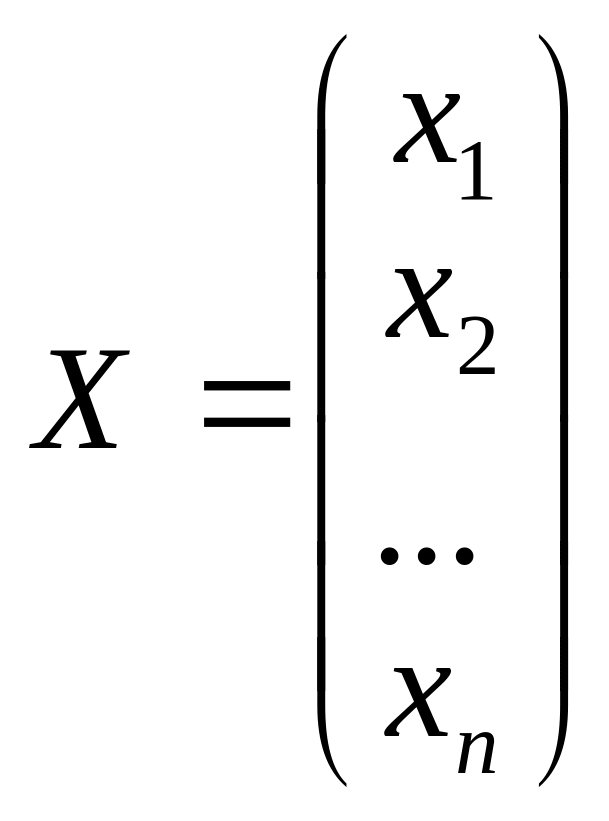 – матрица-столбец
неизвестных,
– матрица-столбец
неизвестных,
 – матрица-столбец
свободных членов системы,
– матрица-столбец
свободных членов системы,
Система
из n уравнений
с n
неизвестными имеет единственное решение
только в том случае, если главный
определитель системы
![]()
Методы решения систем линейных уравнений.
Формулы Крамера
![]() ,
i
= 1,2,…,n
,
i
= 1,2,…,n
где
![]() -
дополнительный определитель матрицы,
отличающейся от матрицы
A тем, что в
ней столбец с номером i
заменен на столбец В.
-
дополнительный определитель матрицы,
отличающейся от матрицы
A тем, что в
ней столбец с номером i
заменен на столбец В.
Возможные случаи:
|
Система имеет единственное решение |
Система совместна и определена |
|
Хотя бы один
|
Система несовместна |
Все
|
Система совместна, но неопределена |
При помощи обратной матрицы.
![]() ,
,
где
![]() - матрица, обратная к
.
- матрица, обратная к
.
Метод Гаусса.
Метод Гаусса или метод последовательного исключения неизвестных заключается в том, чтобы с помощью элементарных преобразований привести расширенную матрицу системы

к ступенчатому виду (получить нули под главной диагональю)
 ,
,
после чего осуществить обратный ход: по матрице, приведенной к ступенчатому виду составить систему уравнений и решить ее.
Элементарные преобразования матрицы:
перестановка строк;
умножение строки на число, отличное от нуля;
сложение строки с другой строкой, умноженной на число.
Тема Аналитическая геометрия
Расстояние
![]() между двумя точками А(хА;
уА)
и
В(хВ;
уВ):
между двумя точками А(хА;
уА)
и
В(хВ;
уВ):
![]() (1)
(1)
Деление отрезка в заданном отношении.
Если точка С
делит отрезок АВ в отношении λ,
начиная от точки A,
т.е.
 ,
то координаты точки C:
,
то координаты точки C:
![]() (2)
(2)
Если точка С делит отрезок АВ пополам, т.е. =1, то координаты точки C:
![]() (3)
(3)
Уравнение прямой на плоскости.
Общее уравнение прямой:
![]() (4)
(4)
Уравнение прямой с угловым коэффициентом:
![]() (5)
(5)
Уравнение прямой с угловым коэффициентом, проходящей через заданную точку
 :
:
![]() (6)
(6)
Уравнение прямой, проходящей через две точки
 и
и
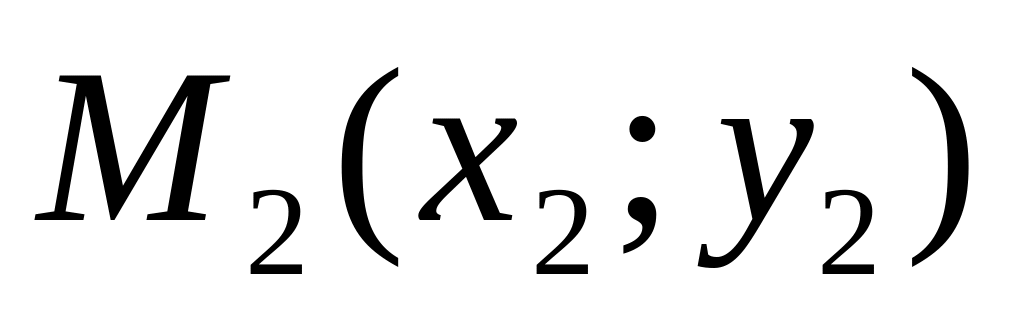 :
:
![]() (7)
(7)
Уравнение прямой в отрезках:
![]() (8)
(8)
Пусть на плоскости заданы две прямые:
![]() и
и
![]()
Условие параллельности прямых на плоскости:
![]() (9)
(9)
Условие перпендикулярности прямых:
![]() (10)
(10)
Тангенс острого угла между пересекающимися прямыми можно найти по формуле:
![]() ,
(11)
,
(11)
откуда
![]() .
.
Уравнение плоскости в пространстве
Общее уравнение плоскости:
![]() (12)
(12)
Уравнение плоскости, проходящей через точку
 перпендикулярно вектору
перпендикулярно вектору
 :
:
![]() (13)
(13)
Вектор называется нормальным вектором плоскости.
Уравнение плоскости, проходящей через три заданные точки

 :
:
 (14)
(14)
Косинус угла между двумя плоскостями, заданными уравнениями
 и
и
 вычисляется как косинус угла между
нормальными векторами заданных
плоскостей:
вычисляется как косинус угла между
нормальными векторами заданных
плоскостей:
![]() (15)
(15)
Уравнение прямой в пространстве
Каноническое уравнения прямой:
![]() (16)
(16)
Вектор
![]() называется направляющим вектором
прямой, он параллелен данной прямой.
называется направляющим вектором
прямой, он параллелен данной прямой.
Уравнение прямой, проходящей через две точки
 и
и
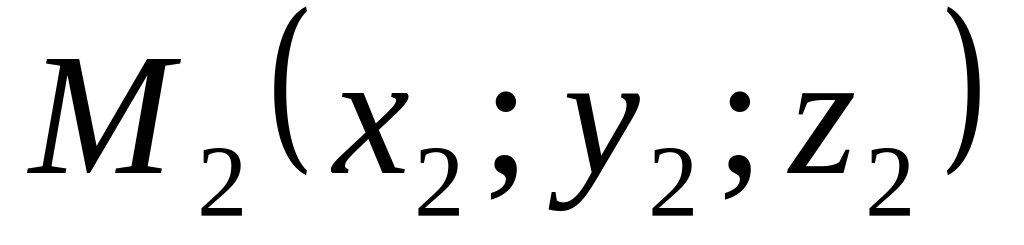 :
:
![]() (17)
(17)
Косинус угла между двумя прямыми вычисляется как косинус угла между направляющими векторами данных прямых:
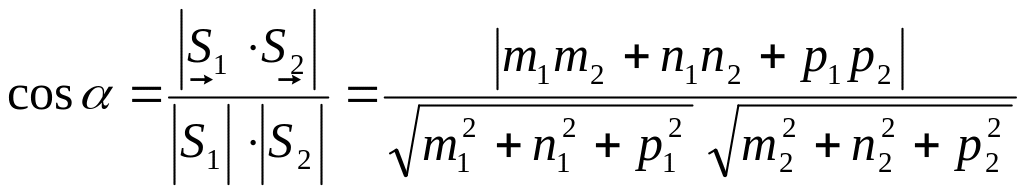 (18)
(18)
Условие перпендикулярности прямых:
![]() ,
(19)
,
(19)
где
![]() ,
,
![]() – направляющие векторы данных прямых.
– направляющие векторы данных прямых.
