Справочный материал Тема Векторы в прямоугольной системе координат.

Вектор в системе координат Oxyz, может быть представлен в виде или .

Модуль вектора .

Пусть даны векторы и , тогда

- сумма векторов

- произведение вектора на число: , где λ – число.

Если известны координаты начала и конца вектора : , , то его координаты можно найти по формуле:

.

Скалярное произведение векторов и – это число, равное произведению модулей векторов на косинус угла между ними:

,

где – угол между векторами a и b.

Если векторы заданы координатами и , тогда

скалярное произведение

Угол между векторами и : .

Для n-мерной прямоугольной системы координат операции сложения, вычитания и вычисления скалярного произведения векторов

Тема Линейная алгебра: матрицы и действия над нами.

Матрицей размера (размерности) называется прямоугольная таблица, содержащая m строк и n столбцов элементов.

Элементы матрицы обозначаются а_ij , где  i - номер строки, j - номер столбца.

Матрица А размером m n имеет вид

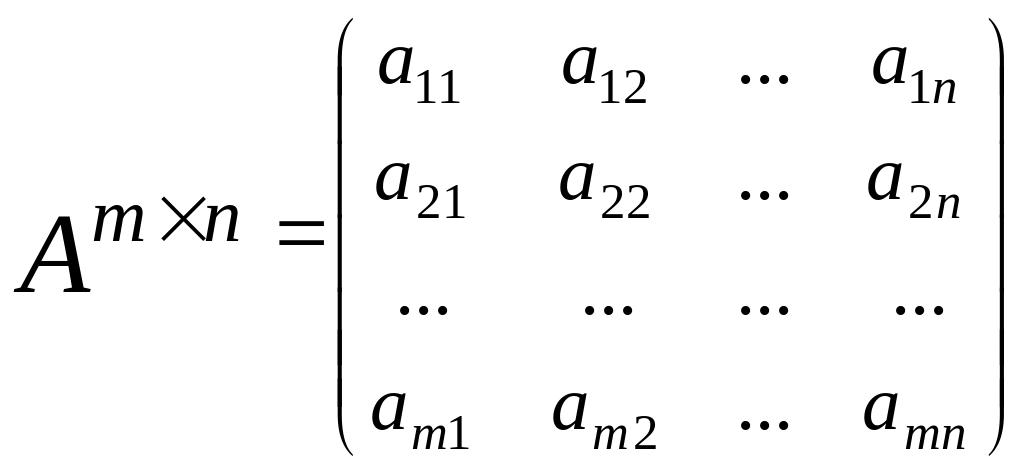
Две матрицы А и В одного размера равны, если их соответствующие элементы равны, т.е. для любых , .

Операции над матрицами

1. Транспонирование.

Транспонированная матрица - матрица, полученная из исходной матрицы А заменой строк на столбцы.

, тогда .

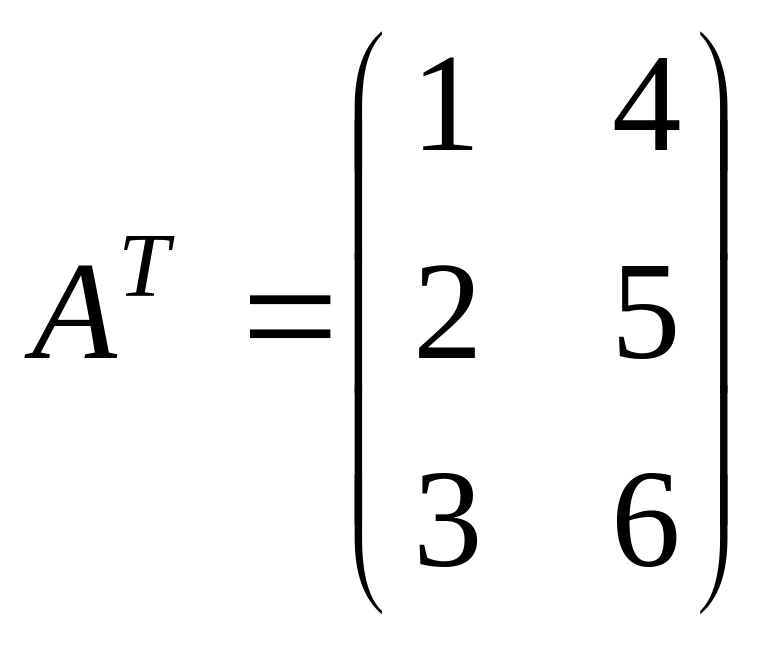2. Умножение матрицы на число.

Чтобы умножить матрицу А на число , нужно каждый элемент матрицы умножить на это число.

, тогда .

3. Сложение матриц.

Операция выполняется для матриц одинаковой размерности.

, , тогда

,

4. Умножение матриц.

Матрицы можно перемножать, если число столбцов первой матрицы равно числу строк второй матрицы.

Элементы матрицы находятся при нахождении суммы произведений строк первой матрицы и столбцов второй матрицы.

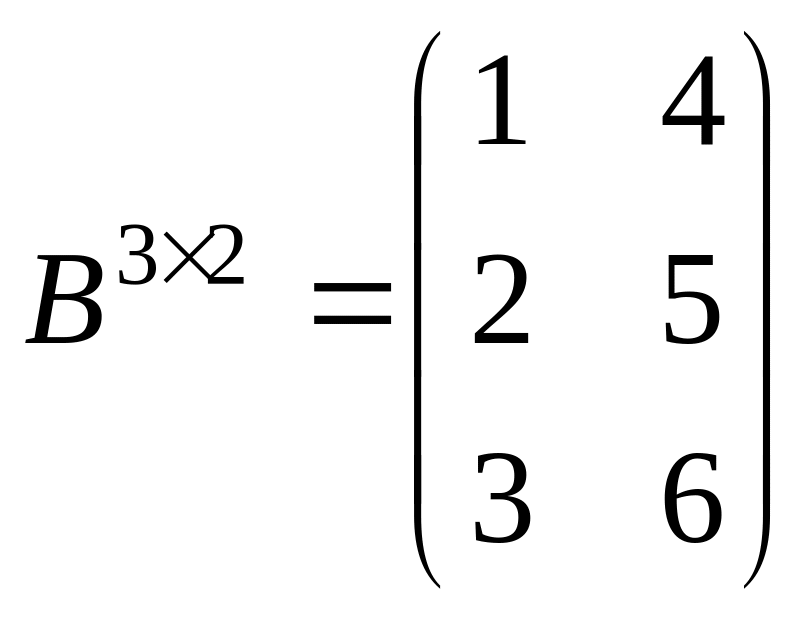, тогда

,

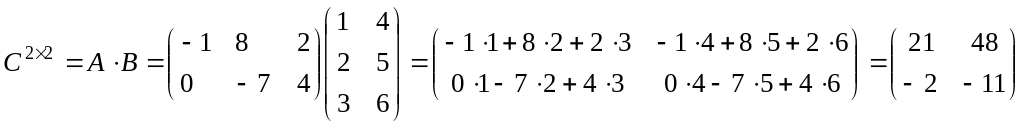Две квадратные матрицы A и B называются коммутирующими, если AB = BA.

5. Возведение в степень.

Например, , тогда .

Тема Линейная алгебра: определители.

Определителем (детерминантом) n–го порядка называется величина, характеризующая квадратную матрицу, которая вычисляется по определенному правилу.

Обозначение определителя матрицы А размером :

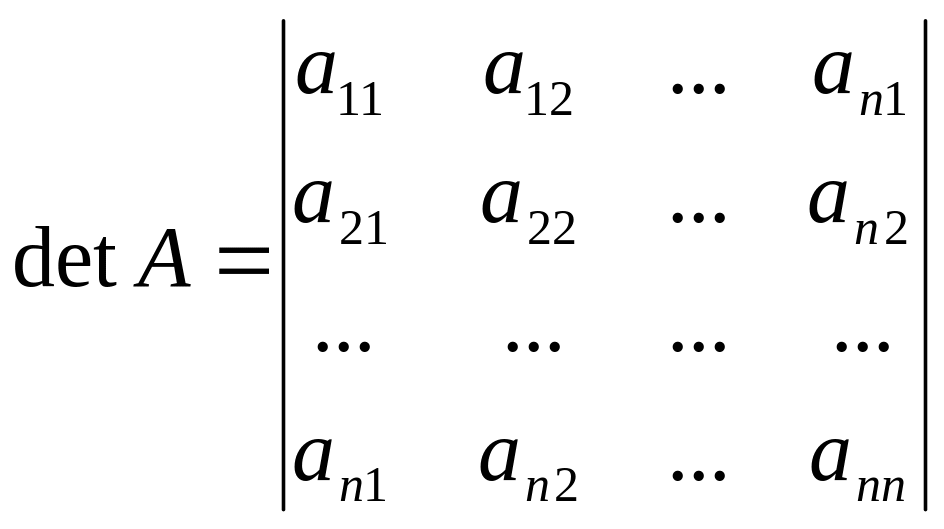или или ∆

Правила вычисления определителей:

1. Определитель квадратной матрицы первого порядка равен ее элементу, т.е. .

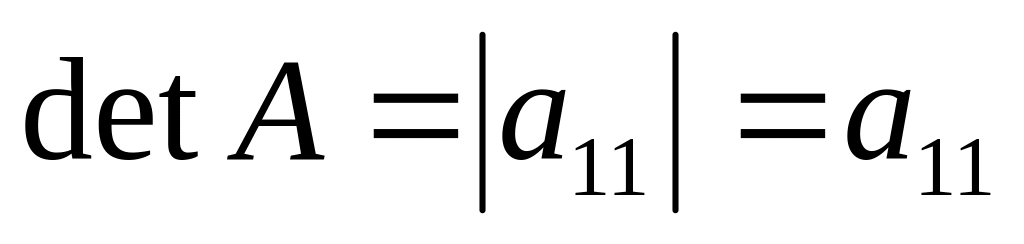2. Определитель квадратной матрицы второго порядка вычисляется по формуле:

.

3. Определитель квадратной матрицы третьего порядка можно вычислить по правилу треугольников:

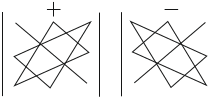
Определитель третьего порядка можно вычислить также разложением по строке или столбцу (см следующее правило):

4. Вычисление определителя квадратной матрицы разложением по строке или столбцу.

Минором M_ij квадратной матрицы n –го порядка называется определитель (n -1)-го порядка, который получается из исходного путем вычеркивания i-й строки и j-го столбца.

Алгебраическим дополнением A_ij элемента a_ij матрицы называется число:

A_ij = (–1)^i+j M_ij.

Например, запишем минор и алгебраическое дополнение к элементу определителя:

,

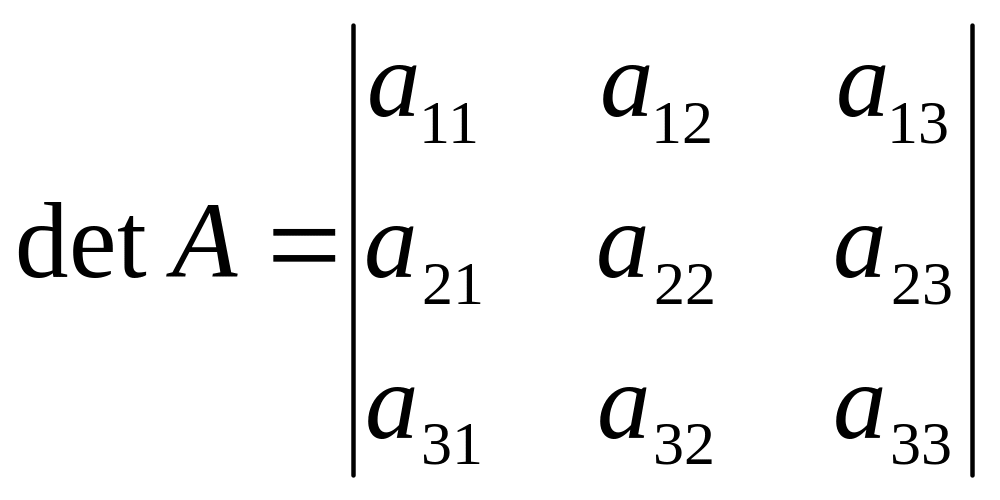
Разложим определитель матрицы по 1 строке:

.

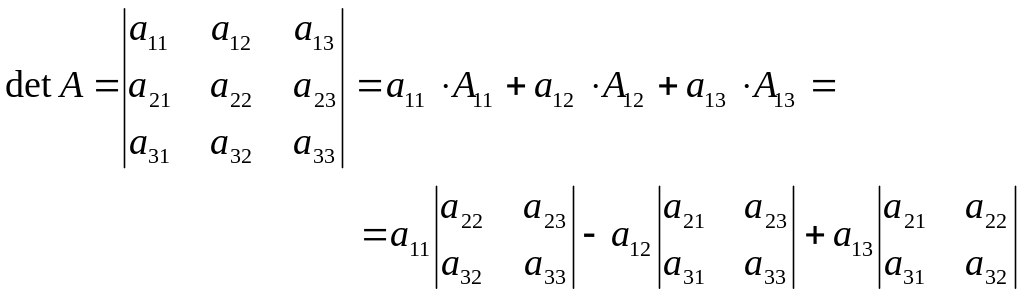
Обратная матрица

Матрица называется обратной для квадратной матрицы , если = =E

Матрица имеет обратную , если . Если , то матрица обратной не имеет.

Алгоритм нахождения обратной матрицы

1. Найти определитель исходной матрицы А и сделать вывод о существовании обратной.

2. Транспонировать матрицу А.

3. Найти алгебраические дополнения элементов транспонированной матрицы и составить из них присоединенную матрицу .

4. Вычислить обратную матрицу по формуле

.

5. Сделать проверку = =E.