Контрольная работа №1

Задача 1

Даны векторы a и b. Найти вектор c = 2a - b , модуль вектора с, скалярное произведение (a, 2b), где a = {1, M+4, -1, N-5} , b = {-M+5, -1, 5 - N, 2}.

Задача 2

1. Найти расстояние между точками А = (N+2, -M-1, N+M) и В = (M, N, M-N).

2. Найти точку пересечения прямых y=-(N+1)x+2 и y=(M+1)x-M-N.

3. Найти уравнение прямой, проходящей через точку (M+1; N+1) и перпендикулярной к прямой y=-2x-1.

4. Написать каноническое уравнение кривой, заданной уравнением 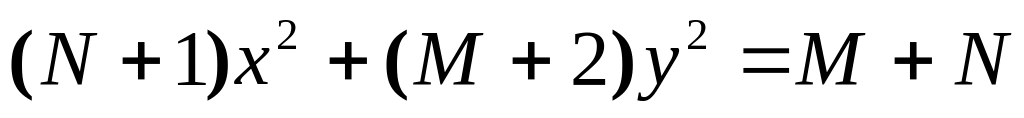. Построить кривую.

Задача 3

Даны матрица размерностью и вектор-строка b. Найти произведения A^T b^T и b  A ; b = {M-5, 1, 4-N}.

Задача 4

Даны матрицы и размерностью . Проверить, коммутативны ли матрицы A и B, и найти определители матриц. Элементы матриц вычисляются по формулам: .

Задача 5

Решить систему из трех уравнений, пользуясь формулой Крамера и методом Гаусса:

Задача 6

Составить систему из двух уравнений с двумя неизвестными так, чтобы она :

a) имела единственное решение;

b) не имела решений;

с) имела бесконечно много решений.

Найти определители этих систем. Учитывая, что каждое из уравнений системы является уравнением прямой линии на плоскости, изобразить эти прямые и пояснить, что означает каждый из трех вариантов с точки зрения взаимного расположения прямых.

Задача 7

Найти пределы:

a) ;

b) ;

c) ;

d) ;

e) ];

f) .

Контрольная работа №2

Задача 1

Найти производные функций:

a) ; b) ;

c) ; d) .

Задача 2

Найти вторую производную функции .

Задача 3

Найти пределы, пользуясь правилом Лопиталя:

а) ; b) .

Задача 4

Исследовать функции и построить их графики :

a) ; b) .

Задача 5

Найти неопределенные интегралы:

a)

b)

c)

d)

Контрольная работа №3

Задача 1

Найти определенные интегралы :

a)

b)

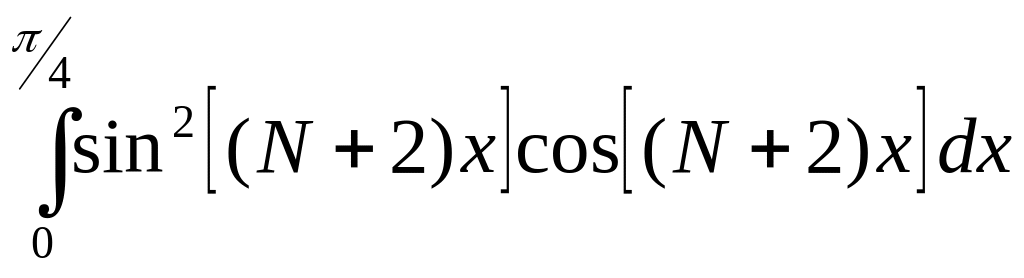
c)

Задача 2

Найти площадь верхней полуволны синусоиды

Задача 3

Найти первые частные производные функций:

a) ;

b) ;

c) ;

d)

Задача 4

Найти полные дифференциалы функций:

a) ;

b) ;

Задача 5

Найти градиент функции в точке ( ):

a)

b)

Задача 6

Исследовать на экстремум функцию:

.

Контрольная работа №4

Задача 1

Найти общее решение дифференциальных уравнений и проверить правильность найденных решений дифференцированием:

a) b) c)

Задача 2

Найти решения дифференциальных уравнений с разделяющимися переменными:

a)

b)

c)

Задача 3

Найти решения линейных уравнений 1 порядка:

a)

b) , y=0 при x=1

Задача 4

Найти решения линейных однородных уравнений с постоянными коэффициентами:

a)

b)

c) с условиями при x = 0 ;

d) .

Задача 5

Найти решения линейных неоднородных уравнений с постоянными коэффициентами в виде суммы общего решения однородного уравнения и произвольного частного решения неоднородного уравнения:

a) , y = 0 при x = 0 ;

b)

Задача 6

Исследовать сходимость следующих рядов:

а) ; б) ; с)

Задача 7

Найти область сходимости степенных рядов:

а) б)

Задача 8

Вычислить с точностью до 0,001

43