Линейные однородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.

Уравнение

(55)

где p и q – вещественные числа, называется линейным однородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами.

Общее решение уравнения (55) имеет вид: ,

где у₁ и у₂ – два линейно независимых частных решения этого уравнения, С₁ и С₂ – произвольные постоянные.

Для нахождения линейно независимых частных решений у₁ и у₂ используется характеристическое уравнение вида

. (56)

В зависимости от корней характеристического уравнения получаются различные виды функций у₁ и у₂ и вид общего решения уравнения (таблица 6).

Таблица 6.

Дискриминант характеристического уравнения	Корни характеристического уравнения	Вид общего решения уравнения
	действительные различные
	действительные равные
	комплексные

Линейные неоднородные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.

Уравнение вида

(57)

где p и q – действительные числа, называется линейным неоднородным дифференциальным уравнением 2-го порядка с постоянными коэффициентами.

Общее решение линейного неоднородного уравнения (57) имеет вид:

(58)

где – общее решение соответствующего однородного уравнения (55), а – частное решение неоднородного уравнения (57).

Построение общего решения неоднородного уравнения состоит из двух этапов. Сначала нужно найти общее решение соответствующего однородного уравнения , затем найти частное решение неоднородного уравнения.

Для нахождения частного решения уравнения можно использовать метод неопределенных коэффициентов.

1. Если , то частное решение можно искать в виде:

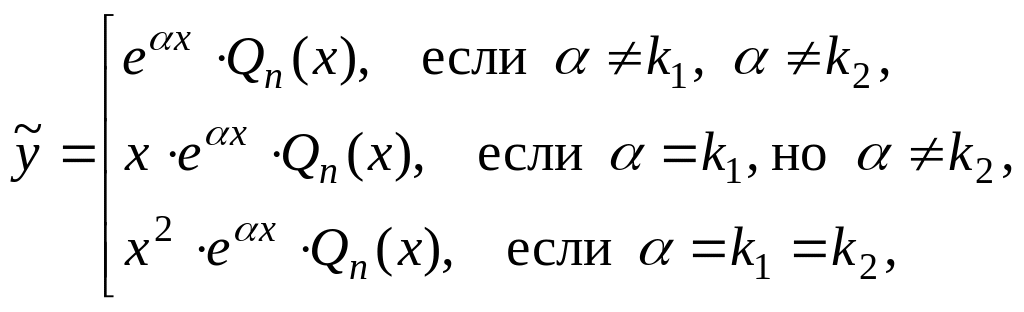(59)

где k₁, k₂ – корни характеристического уравнения, Q_n(x) – многочлен степени n.

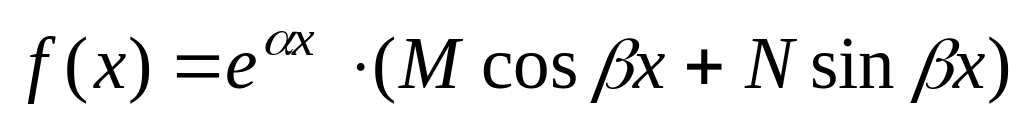2. Если , то частное решение можно искать в виде:

(60)

где k₁, k₂ – корни характеристического уравнения, А и В – неизвестные постоянные.

Тема Ряды

Числовым рядом называется выражение вида

, (61)

где u₁, u₂, u₃,…, u_n,… - действительные или комплексные числа, называемые членами ряда. u_n – общий член ряда.

Ряд считается заданным, если известен общий член ряда .

Сумма первых n членов ряда называется n-ной частичной суммой ряда и обозначается S_n.

(62)

Предел последовательности частичных сумм ряда (61) при , если он существует, называется суммой ряда, т.е.

Если существует, то ряд (61) сходится. В противном случае ряд (61) расходится.

Необходимый признак сходимости

Если ряд

сходится, то его общий член при стремится к нулю, т.е. .

Достаточные признаки сходимости знакоположительных рядов

Знакоположительным называется ряд с неотрицательными членами.

Первый признак сравнения.

Пусть даны два ряда с положительными членами:

(63)

и

, (64)

причем , Тогда если сходится ряд (64), то сходится и ряд (63); если расходится ряд (63), то расходится и ряд (64).

Второй признак сравнения (в предельной форме).

Пусть для рядов (63) и (64) существует предел

.

Тогда если , то либо оба ряда сходятся, либо расходятся одновременно; если и ряд (64) сходится, то сходится и ряд (63). Если же и ряд (64) расходится, то расходится и ряд (63).

Стандартные ряды, применяемые для признаков сравнения:

Гармонический ряд: - расходится.

Обобщенный гармонический ряд (ряд Дирихле): расходится при и сходится при .

Ряд геометрической прогрессии при сходится, при расходится.

Признак Даламбера.

Пусть дан ряд с положительными членами и существует конечный или бесконечный предел

, (65)

то этот ряд сходится при и расходится при .

При признак Даламбера не дает однозначного ответа о сходимости.

Радикальный признак Коши.

Пусть дан ряд с положительными членами и существует конечный или бесконечный предел

, (66)

то этот ряд сходится, если , и расходится, если .

При признак Коши не дает однозначного ответа о сходимости.

Интегральный признак Коши.

Если члены знакоположительного ряда могут быть представлены как числовые значения некоторой непрерывной монотонно убывающей при функции , то если сходится несобственный интеграл , то сходится и ряд (61). Если же интеграл расходится, то расходится и ряд (61).

Знакочередующиеся ряды, их абсолютная и условная сходимости. Признак Лейбница.

Числовой ряд называется знакочередующимся, если он содержит как положительные, так и отрицательные члены, которые следуют друг за другом поочередно.

(67)

Признак сходимости знакочередующегося ряда (признак Лейбница). Знакочередующийся ряд сходится, если абсолютные величины его членов монотонно убывают, и общий член ряда по модулю стремится к нулю.

Для сходимости знакочередующегося ряда (67) достаточно выполнения двух условий:

1) ;

2) .

При этом, если ряд (67) сходится по признаку Лейбница и сходится ряд, составленный и модулей его членов

, (68)

то говорят, что ряд (67) сходится абсолютно. Если же ряд (68) расходится, то ряд (67) сходится условно (может как сходиться, так и расходиться).

Функциональные ряды.

Ряд, членами которого являются функции от , называется функциональным:

, (69)

Значение , при котором ряд (69) сходится, т.е. сходится числовой ряд , называется точкой сходимости функционального ряда.

Множество значений аргумента , при которых функции определены, и ряд сходится, называется областью сходимости функционального ряда.

Функция называется остатком функционального ряда.

Степенные ряды. Радиус и область и сходимости степенного ряда.

Степенным рядом называется функциональный ряд вида

, (70)

где a, A₀, A₁, A₂, …, A_n, … - действительные числа. Частный случай степенного ряда при :

.

Теорема Абеля. Если степенной ряд (14) сходится при , то он сходится, причем абсолютно, при любом x, удовлетворяющем неравенству

(71)

Если же ряд (14) расходится при , то он расходится и при любом x, удовлетворяющем неравенству

(72)

Из теоремы Абеля следует, что существует симметричный интервал абсолютной сходимости степенного ряда относительно точки , которая называется центром сходимости. Половина длины интервала называется радиусом сходимости и обозначается R.

Радиус сходимости R может принимать значения . Сходимость ряда в точках и исследуется дополнительно и добавляется к интервалу, образуя область сходимости.

Радиус сходимости находится по формуле

(73)

Или при применении радикального признака Коши:

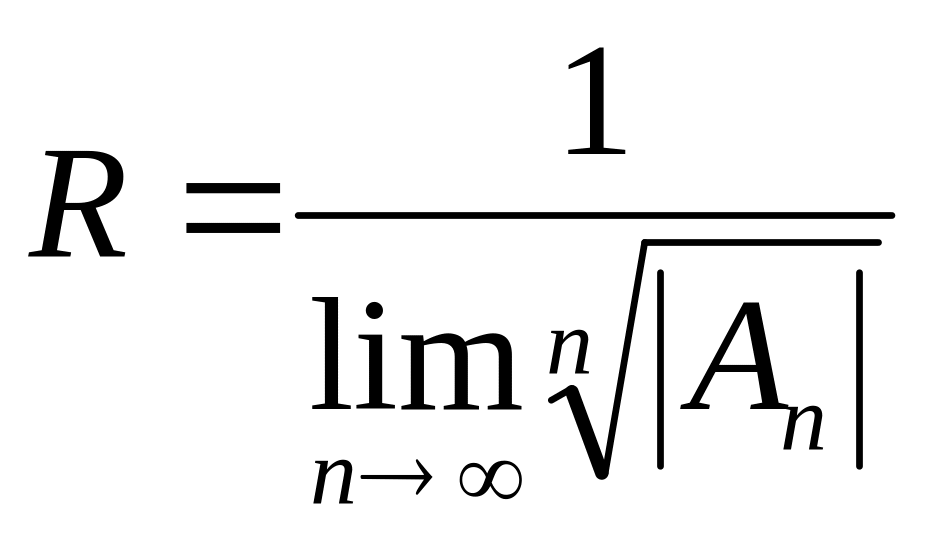(74)

Ряды Тейлора и Маклорена.

Рядом Тейлора для функции называется степенной ряд

(75)

Частным случаем ряда Тейлора при является ряд Маклорена:

(76)

При разложении функций в ряд удобно применять ряды Маклорена для некоторых элементарных функций, представленные ниже:

.

.

. ;

.

.

Последний ряд называется биномиальным, частные случаи которого представлены ниже:

.

.

Приложения степенных рядов для приближенного вычисления функций и определенных интегралов.

Для вычисления значения приближенного функции при данном значении аргумента можно воспользоваться разложением этой функции в степенной ряд, удобно воспользоваться разложениями в ряд Маклорена элементарных функций.

Для приближенного вычисления определенного интеграла нужно разложить в степенной ряд подынтегральную функцию, проинтегрировать степенной ряд почленно и сохранить в ряде достаточное количество его первых членов (для обеспечения заданной точности).