Уравнения с разделяющимися переменными.

Дифференциальное уравнение вида

или (44)

называется дифференциальным уравнением с разделяющимися переменными.

Для того, чтобы решить уравнение (44), нужно разделить переменные x и y, т.е. собрать в левой и правой его частях функции, зависящие только от одной переменной.

Заменим производную на и разделим переменные. Получим:

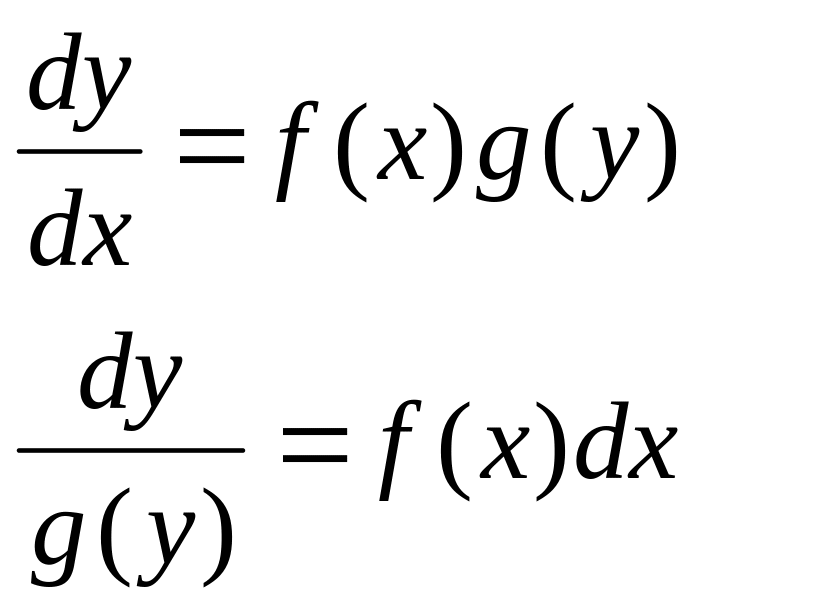
Решение этого уравнения находим почленным интегрированием левой и правой частей:

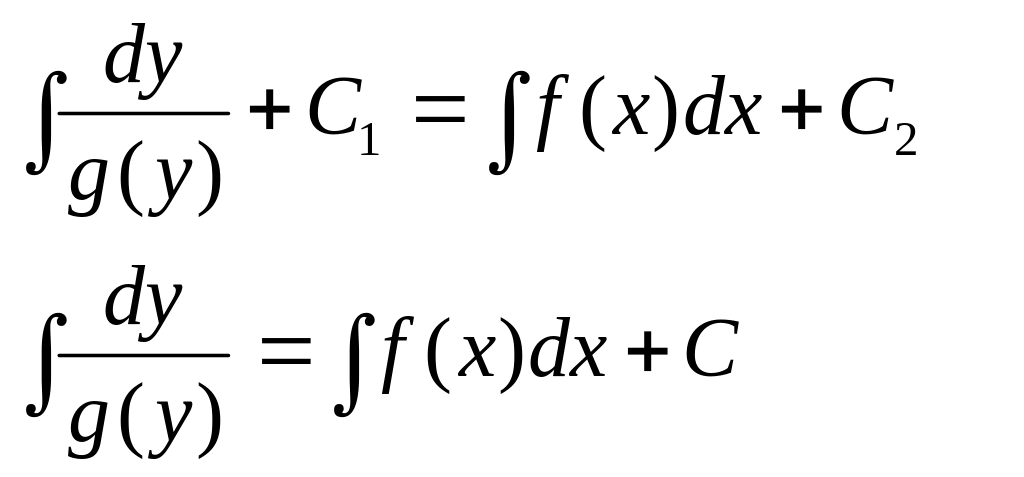
где С = С₂ – С₁.

Линейные дифференциальные уравнения 1-го порядка.

Дифференциальное уравнение вида

(45)

где p(x), q(x) – заданные функции, называется линейным дифференциальным уравнением 1-го порядка.

Для решения уравнения (45) воспользуемся способом подстановки. Будем искать неизвестную функцию y в виде y = u(x)v(x). Тогда Подставим значения y и в уравнение (45):

(46)

Выберем v(x) так, чтобы выражение в скобках обратилось в нуль, т.е.

, (47)

тогда из (46) получится уравнение

(48)

Оба уравнения (47) и (48), являются дифференциальными уравнениями с разделяющимися переменными. Общее решение исходного уравнения запишется как произведение частного решения уравнения (47) и общего решения уравнения (48):

(49)

Уравнение Бернулли.

Дифференциальное уравнение вида

(50)

где n – действительное число, , называется уравнением Бернулли.

Уравнение Бернулли решается тем же способом, что и линейное дифференциальное уравнение 1-го порядка.

Однородные уравнения.

Функция называется однородной функцией m-го порядка, если при умножении каждого ее аргумента на произвольный множитель вся функция умножится на , т.е.

Дифференциальное уравнение вида

P(x,y)dx+Q(x,y)dy = 0 (51)

называется однородным, если P(x,y) и Q(x,y) – однородные функции одного порядка.

Однородное дифференциальное уравнение может быть приведено к виду

(52)

При помощью подстановки , т.е. однородное дифференциальное уравнение приводится к уравнению с разделяющимися переменными относительно новой функции t.

Дифференциальные уравнения 2-го порядка

Дифференциальным уравнением 2-го порядка называется уравнение вида

(53)

где х – независимая переменная, y – неизвестная функция этой переменной, и – ее производные.

Общее решение уравнения 2-го порядка имеет вид:

y = g(x, C₁, C₂), (54)

где С₁ и С₂ – две произвольные постоянные.

Задача Коши для дифференциального уравнения 2-го порядка (53) состоит в нахождении частного решения уравнения, удовлетворяющего двум начальным условиям . Для решения задачи Коши нужно подставить в общее решение (54) и его производную заданные начальные условия, решить полученную систему двух уравнений относительно неизвестных С₁ и С₂ и подставить найденные значения постоянных в общее решение.