Тема Функции многих переменных

Функция f есть функция двух переменных x и y, если каждой паре значений из некоторого множества D соответствует определённое значение величины f. Множество D называется областью определения функции .

Если одной из переменных функции придать приращение, а другую переменную не изменять, то функция получит частное приращение по одной из переменных: и

Частной производной функции нескольких переменных называется предел отношения частного приращения функции к соответствующему приращению переменной при условии, что приращение переменной стремится к нулю:

– частная производная функции z по переменной x;

– частная производная функции z по переменной у.

При вычислении частной производной по одной переменной, все остальные переменные следует считать постоянными и проводить дифференцирование по правилам дифференцирования функции одной переменной.

Полный дифференциал функции выражается формулой:

(42)

Производные фнп высших порядков

Так как и являются функциями переменных x и y, то их можно дифференцировать по x и по y. Эти частные производные от функции называются частными производными второго порядка

Экстремумы фнп

Функция имеет максимум в точке , если существует такая окрестность точки , в которой выполнено неравенство для всех точек из этой окрестности, отличных от .

Функция имеет минимум в точке , если существует такая окрестность точки , в которой выполнено неравенство для всех точек из этой окрестности, отличных от .

Максимум и минимум называют экстремумами ФНП.

Необходимое условие экстремума ФНП: если функция имеет экстремум в точке , то ее частные производные первого порядка в этой точке равны нулю.

Точки, в которых выполняется необходимое условие, называются критическими точками функции.

Достаточное условие экстремума ФНП: Вычислим в критической точке значения , , . Обозначим . Значение показано в таблице 5.

Таблица 5

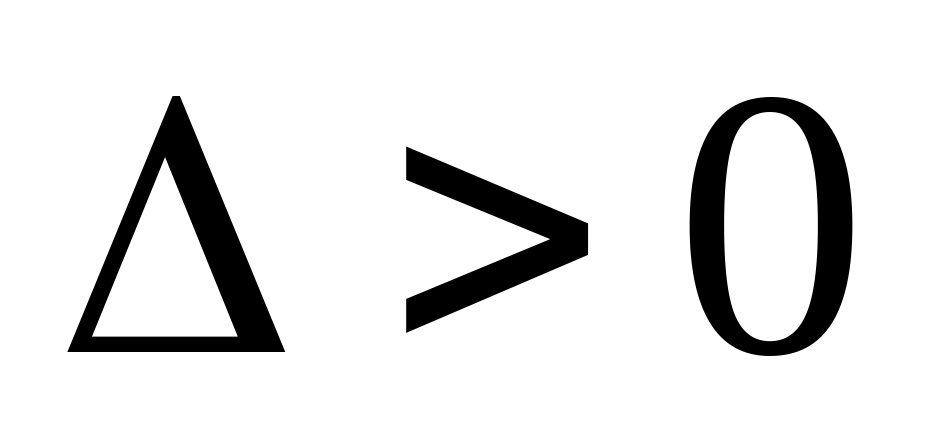
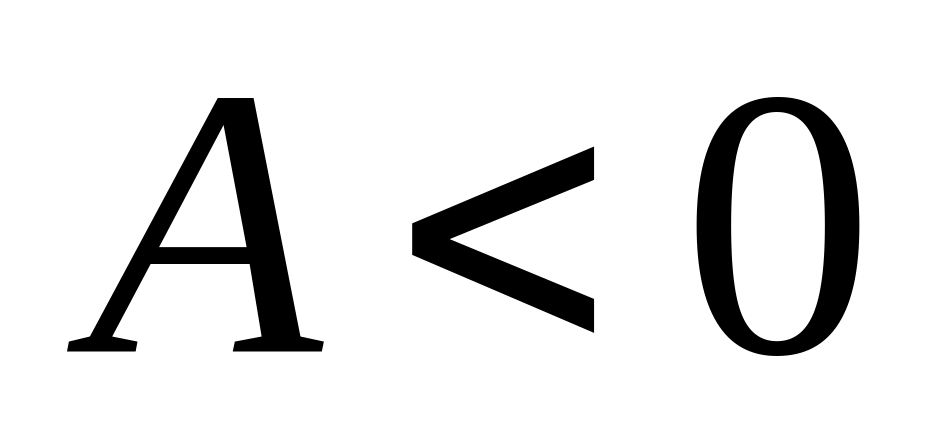
		В точке минимум В точке максимум
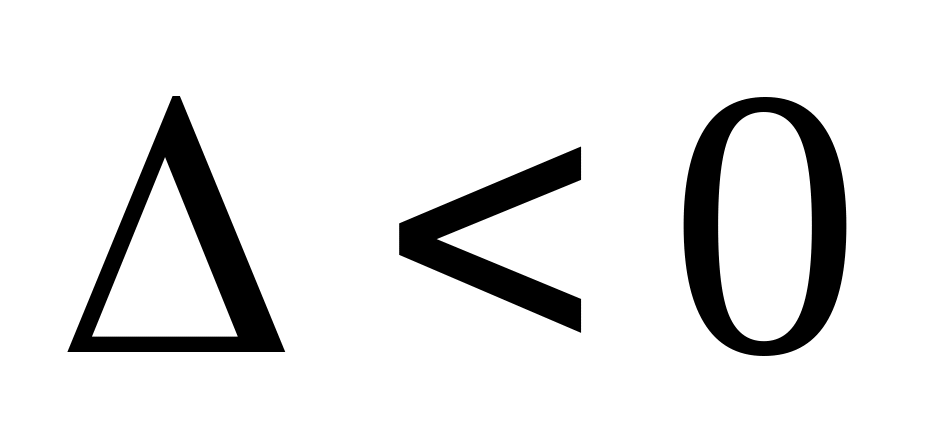
	В точке функция экстремума не имеет
	В точке экстремум может быть, а может не быть. Необходимы дополнительные исследования.

Тема Дифференциальные уравнения

Дифференциальным уравнением 1-го порядка называется уравнение вида

(43)

где x – независимая переменная, y – неизвестная функция этой переменной, – ее первая производная.

Если уравнение можно разрешить относительно , то его записывают .

Решением дифференциального уравнения называется функция - первообразная для функции , которая при подстановке в дифференциальное уравнение обращает его в тождество.

Общее решение дифференциального уравнения 1-го порядка записывается в виде , где С – произвольная постоянная.

Задача нахождения частного решения дифференциального уравнения, удовлетворяющего начальному условию, называется задачей Коши. Чтобы найти частное решение дифференциального уравнения (43), удовлетворяющее начальному условию y(x₀) = y₀, нужно в общее решение уравнения подставить x = x₀, y = y₀ и из полученного уравнения найти C, затем найденное значение C подставить в общее решение.

Общее решение задает на плоскости XOY семейство интегральных кривых данного дифференциального уравнения. Решению задачи Коши соответствует одна интегральная кривая из этого семейства, проходящая через точку (x₀; y₀).