10. Траектория, ағын сызығы мен құйын сызығы және олардың дифференциалдық теңдеулері.

Тұтас орта қозғалысын зерттегенде 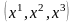немесе координаталарының функциялары болатын скалярлық және векторлық шамаларды ендіру қажет. Осы әрбір координаталар жүйесінен белгілі бір облысты бөліп алып және осы облыстың әрбір нүктесіне сәйкес температураның 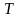, жылдамдықтың немесе одан да күрделі характеристикалардың сан мәнін қоюға болады. Қарастырылып отырған облыстың әрбір нүктесінде берілген шамалар мәндерінің жиынтығы сол шамалардың (скалярлық, векторлық) өрістері деп аталады.

Температура және жылдамдық өрістерінің мысалынан олардың кейбір ортақ характеристикаларын зерттейік. Егер температураның таралуы Лагранж айнымалылары арқылы берілсе, онда тұтас орта бөлшектерінің бірлік уақыттағы температурасының өзгерісін есептеу оңай. Ол температурадан уақыт бойынша алынған туындыға тең.

Егер температураның таралуы Эйлер айнымалылары арқылы берілсе, онда бұл туындыны есептегенде Лагранж айнымалыларына көшіп

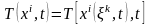
және күрделі функцияны дифференциалдау ережесін пайдалану қажет. Сонда

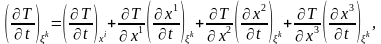
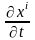туындысы тұрақты болған жағдайда алынады және жылдамдық векторының компоненттері болып табылады. Сондықтан

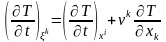
немесе

.

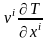туындысы тұтас ортаның берілген нүктесіндегі уақытқа байланысты температураның өзгерісін сипаттайды және уақыт бойынша температураның толық туындысы делінеді. туындысы кеңістіктің берілген нүктесіндегі бірлік уақыттағы температураның өзгерісін сипаттайды және локальдық туынды деп аталады. туындысы кеңістіктің бір нүктесінен белгіленген уақыт мезетінде оған шексіз жақын жатқан нүктеге орын ауыстырғандағы температураның өзгерісін сипаттайды және конвективті туынды деп аталады. Егер процесс стационар болса, онда оларды сипаттайтын барлық шамалардан уақыт бойынша алынған локальдық туынды нольге тең

.

Конвективті туынды қозғалыс болмаған жағдайда немесе температураның градиенті жоқ кезде, яғни температураның скаляр өрісі біртекті болғанда нольге тең

.

Кез келген векторлық өріске мысалы, жылдамдық өрісі үшін енгізуге болатын векторлық сызықтардың мағынасын зерттеуге көшейік. Практикада көбінесе ағын сызықтарын білу қажет. Ағын сызығының қасиеті – берілген уақыт мезетінде жылдамдық векторы ағын сызығының барлық нүктесіне жанама болып келеді. Осы анықтамадан ағын сызықтарының бойынан алынған элемент

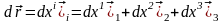
және жылдамдық векторы

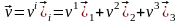
бір-біріне параллель, яғни

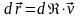
мұндағы –скаляр параметр. Ал енді жылдамдықтың компоненттері арқылы жазсақ

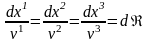
немесе

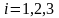. (1)

Бұл ағын сызығының дифференциалдық теңдеуі. Ол орта бөлшектерінің қозғалыс траекториясының дифференциалдық теңдеуінен өзгеше

. (2)

(1) теңдеуін интегралдағанда t тұрақты параметр деп, ал (2) теңдеуіндегі t айнымалы деп есептеу қажет.

Стационар қозғалыс кезінде ағын сызығы мен траектория бір - бірімен беттеседі.

“C” контурдың әрбір нүктесі арқылы ағын сызықтарын жүргізуге болады. Егер “C”-ның өзі ағын сызығы болмаса, онда ағын сызығының беті пайда болады. Егер “C” контуры тұйық болса, онда ағын түтікшесі делінеді. Ағын түтікшесінің ішіндегі сұйықтың шығымы тұрақты болады. Кез келген векторлық өрісте осындай жолмен жасалынған түтікше векторлық түтікше деп аталынады.

Кез келген векторлық өріс сияқты, құйын жылдамдығы векторының өрісі үшін де құйын сызықтары мен түтікшелері ұғымын енгізуге болады. Құйын сызығының барлық нүктесіне құйын векторы 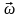жанама болып келеді. Құйын сызығының дифференциалдық теңдеуі

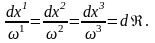(3)

Құйын сызықтарына жоғарыда айтылған ағын сызықтарының барлық қасиеттері сәйкес келеді.

11,12,13. Үзіліссіздік теңдеуі.

Үзіліссіздік теңдеуі

Тұтас орта механикасы курсында негізінен материалдық денелердің қозғалыс заңдары қарастырылады. Материалдық денелер деп, инерция қасиеттеріне ие бола алатын денелерді айтады. Математикалық тұрғыдан инерцияның қасиеті массамен сипатталады. m массаны толық V көлем үшін және сол сияқты оның кез келген бөлшектері үшін де енгізуге болады

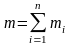
Теориялық механикада көлемсіз материалдық нүктеге белгілі бір m масса тағайындалады. Сонымен материалдық нүкте деген феноменологиялық ұғым енгізіледі. Ал тұтас орта механикасында мұндай ұғым қолданылмайды. Нақты дененің үздіксіз материямен толтырылған көлемінің инерттілік қасиеті ортаның нүктелерімен байланысты емес, себебі нүктенің өлшемі жоқ, яғни массасы да болмайды. Бірақ тұтас орта динамикасының теңдеуі ортаны толтырып тұрған кез келген нүкте үшін орындалатын ортаның қозғалыс заңдылығын өрнектейді. Сондықтан тұтас орта механикасы субстанциялардың (масса, күш, энергия және т.б.) өздерімен емес, олардың берілген ортадағы тығыздығының таралуымен анықталады.

Тұтас орта механикасында массаның орнына төмендегідей жолмен анықталатын ортаның тығыздығы 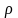ұғымы қолданылады

.

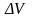көлеміндегі массаның жайғасуын заттардың орташа тығыздығы деп атайды. Берілген нүктедегі ортаның нақты тығыздығы келесі шек арқылы анықталады:

.

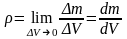Ортаның тығыздығы Лагранж және Эйлер айнымалыларының скаляр функциясы болып табылады

.

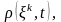
Егер көлемнің әрбір нүктесінде тығыздықтың мәндері белгілі болса, онда тығыздықтың скаляр функциясының өрісі тығыздық өрісі деп аталады. Егер тығыздықтар өрісі 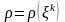немесе уақытқа тәуелсіз болса, онда тығыздықтар өрісі стационар деп аталады. Егер тығыздықтар 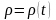өрісі x^k координаталарға тәуелсіз, тек қана уақытқа t тәуелді болса ондай өрісті біртекті өріс дейді.

Шынында да 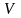көлемді алып жатқан ортаның тығыздықтар өрісі белгілі болса, онда дененің толық массасы төмендегі интеграл арқылы табылады

.

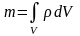Массаның сақталу заңы Ньютон механикасының іргелі заңдарының бірі. «Тұтас ортаның біртекті бөлшектерінен тұратын кез келген жеке көлемінің массасы қозғалыс кезіндегі барлық уақытта тұрақты болады». Бұл анықтама релятивтік жуықтауда орындалатын тәжірибе арқылы тағайындалған табиғат заңы. Кез келген шаманың өзгерісі уақыт бойынша алынған дербес туындымен сипатталатындықтан массаның сақталу заңы математикалық түрде былай жазылады

немесе . (1)

Тұтас ортада тығыздық мен жылдамдықтың таралуына массаның сақталу принципі белгілі бір шектеу жасағанмен, (1) арақатынасы универсал болып табылады. Ол кез келген орта мен қозғалыс үшін және үздікті қозғалыс жағдайында да орындалады. (1) теңдеуі үзіліссіз қозғалыс үшін мен -ны байланыстыратын, үзіліссіздік теңдеуі деп аталынатын теңдеу түрінде де өрнектеледі. Үзіліссіздік теңдеуі тұтас орта механикасындағы ортаның тұтастық шартын өрнектейтін негізгі динамикалық теңдеулердің бірі болып табылады. Оны Лагранж айнымалылары, сол сияқты Эйлер айнымалылары арқылы да жазуға болады.

Лагранж айнымалылары

Егерд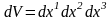е , және 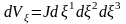екендігін ескерсек, мұндағы – координаталар өзгерісінің якобианы, массаның сақталу принципі (1) мына түрде жазылады

.

Интегралдық формадағы үзіліссіздік теңдеуі, тұтас ортаның жеке көлеміндегі 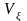массасы өзгермей сақталатындығын көрсетеді. Бұл шартты пайдалану үшін интегралданатын функция болса жеткілікті. Егер тығыздық пен жылдамдық үздіксіз және Лагранж айнымалылары бойынша туындылары үздіксіз мәнге ие болса, онда интегралдық шартты дифференциалдық арақатынаспен ауыстыруға болады. Шынында да, уақыт бойынша алынған туындыны интеграл белгісінің астына енгізсек

.

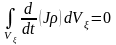Бұдан көлем кез келген мәнге ие бола алатындықтан

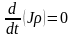. (2)

Бұл дифференциалдық теңдеу Лагранж айнымалылары арқылы жазылған дифференциалдық формадағы үзіліссіздік теңдеуі болып табылады. Интегралдағаннан кейін Лагранж айнымалылары түріндегі үзіліссіздік теңдеуге келеміз

,

мұндағы «0» индексімен уақыт мезгіліне, яғни , 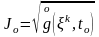сәйкес шамалардың мәндері белгіленген:

.

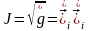Егер кез келген жекеленген көлем уақыт өтуіне байланысты өзгермейтін болса, ондай тұтас орта сығылмайтын орта делінеді, яғни

немесе 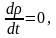бұдан .

Сығылмайтын ортадағы тығыздық тек Лагранж координатасының функциясы болса уақытқа тәуелсіз, яғни сығылмайтын ортадағы белгіленген бөлшектердің тығыздығы қозғалыстың барлық уақытында да өзгермей тұрақты болып қалады. Егер орта біртекті болса, онда тығыздық тұрақты болады.

Эйлер айнымалылары түріндегі үзіліссіздік теңдеуі

Енді үзіліссіздік теңдеуінің түрін Эйлер айнымалылары арқылы табайық. Массаның сақталу заңына (1)-ге сүйенсек, қозғалмалы көлем арқылы алынған интеграл нольге тең

.

Көлемді өз еркімізше таңдап алуға болғандықтан, Эйлер айнымалылары арқылы өрнектелген Эйлердің үзіліссіздік теңдеуіне келеміз

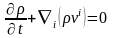. (3)

Бұл теңдеуді тұтас орта механикасының негізгі дифференциалдық теңдеуі деп те атайды. Векторлық анализ ережесін пайдаланып және толық туынды ұғымын ескеріп (3) формуласын мына түрде жазуға болады

.

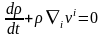(3) теңдеуінің тік бұрышты декарт координаталар жүйесіндегі түрі

.

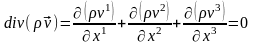Егер орта сығылмайтын болса, онда үзіліссіздік теңдеуі мынаны береді

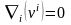. (3)’

Тік бұрышты декарт координаталар жүйесінде жоғарғы теңдеу мына түрде жазылады

.

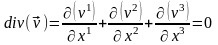Бұл арақатынас сығылмайтын ортаның жылдамдық өрісі соленоидті өріс болып табылатындығын білдіреді.

Үзіліссіздік теңдеуінің (3) түрі ортаның қасиеттеріне тәуелсіз (ауа, су, сұйық металл т.б.) универсалдық сипатта болады және кез келген материалдық ортаның қозғалысында орындалады.

Үзіліссіздік теңдеуіне сығылатын орта жағдайында төрт 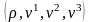, ал сығылмайтын орта жағдайында үш белгісіз функциялар кіреді.

Тұтас орта механикасының есептерін шешу үшін жалғыз үзіліссіздік теңдеуі, яғни массаның сақталу заңы жеткіліксіз. Оны қозғалыс мөлшерінің сақталу заңы, қозғалыс мөлшері моментінің сақталу заңының теңдеулерімен толықтыру қажет. Сол себепті ортаға әсер ететін әртүрлі күштер арқылы анықталатын тұтас орта қозғалысының заңдылықтарын сипаттайтын теңдеулерді қорытуды қарастырайық.