6. Орын ауыстыру векторының компоненттері арқылы деформация тензорын өрнектеу

Евклид метрикасында нақты орындалатын бастапқы 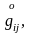күйден күйіне ауысуды қарастырайық. Бұл жағдайда орын ауыстыру векторын енгізуге болады, сонда . Мұндағы 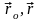- бастапқы және берілген уақыт мезетіне сәйкес, тұтас ортаның бір ғана M нүктесінің 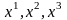-ке қатысты санақ жүйесінің радиус-векторлары. Сонда төмендегі өрнекті алу қиын емес

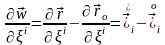
бұдан 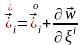немесе

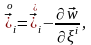
сондықтан

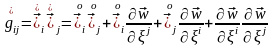
ал

сол себепті деформация тензоры былай өрнектеледі

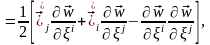(1)

мұндағы -ден координатасы бойынша алынған бірінші туынды тұтас орта нүктесінің салыстырмалы орын ауыстыруын сипаттайды.

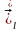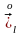орын ауыстыру векторын, актуальді кеңістікте, сол сияқты бастапқы кеңістікте жіктеп, соған сәйкес векторының екі түрлі компоненттерін

,

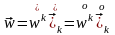сонымен қатар екі түрлі ковариантты туындыны да енгізуге болады

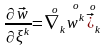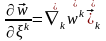және . (2)

(2)- дегі бірінші өрнекті (1)-ге қойып мынаны аламыз

.

Метрикалық тензордың қасиеттерін пайдаланып төмендегідей формулаға келеміз

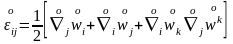. (3)

Сол сияқты (2)- дегі екінші өрнекті (1)-ге қойып, мына өрнекті аламыз

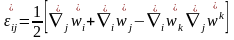(4)

Шексіз аз салыстырмалы орын ауыстыру жағдайында соңғы квадраттық мүшелерді ескермеуге болады

. (5)

Декарт координаталар жүйесінде

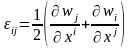. (6)

Соңғы (6) формуладан деформация тензорының симметриялылығы көрініп тұр.

Ескерте кететін жай, деформация тензорының компоненттері үшін (1), (3) және (4) формулалары, қозғалыстағы ортаның барлық нүктелеріне орын ауыстыру векторын енгізуге болатын кезде ғана орындалады. Орын ауыстыру векторының бар-жоқтығы белгісіз жағдайда да деформация тензоры және оның компоненттері 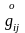, метрикалары арқылы анықталады.

7. Деформация тензорының бас осьтері .Деформация тензорының бас компоненттері. Көлемдік ұлғаю коэффициенті

Әрбір симметриялық тензормен, соның ішінде деформация тензорымен квадраттық форманы 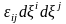байланыстыруға болады. Кез келген нүктеде ортогональ координаталар жүйесін 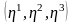табуға мүмкін болса, квадраттық форма мына түрге келеді

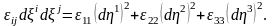
- ден 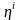-ға түрлендіру компоненттеріне байланысты. Сондықтан әр уақыт мезетіне сәйкес қозғалыстағы ортогональді триэдр жалпы айтқанда әртүрлі болады.

Егер кеңістігінде ортогональ осьтер , , 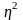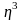табылса және олар қозғалыс нәтижесінде кеңістігіндегі 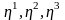осьтердің бағыттарына өткенде базис векторлары ортогональ болып қалса, ондай осьтер деформация тензорының бас осьтері деп аталады. Сонымен қиғаштану бұрышы және

= = =0, .

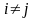Сол себепті бас осьтердің арасындағы бұрыштар қиғаштанбайды және бас осьтердің ортогональ триэдрі абсолют қатты дене сияқты орын ауыстырады, яғни ілгерілемелі ығысады және айналады. Бұл кезде бас осьтердің бойынан алынған элементі, қозғалыс кезінде сығылуы немесе созылуы мүмкін.

Деформация тензорының бас осьтері және 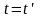уақыт мезгілдерінде ортаның сол баяғы жеке бөлшектері арқылы өтеді.

уақыт мезетінде деформация тензорының бас осьтері бойымен

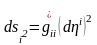
және бас осьтердегі ұзындықтың квадратын төмендегідей түрге келтіруге болады

.

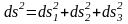Сол сияқты «бастапқы күйде» төмендегі теңдіктер орындалады

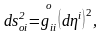
Қарастырылып отырған нүктенің маңында бас осьтер бойынан алынған элементар кесінділер және тап осы күйде және соған сәйкес белгілі «бастапқы күйде» кәдімгі тік бұрышты декарт координатасы ретінде қарастырылады.

Деформация тензорының ковариантты компоненттерінің анықтамасын пайдалансақ

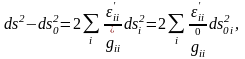
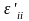-дегі штрих деформация тензорының ковариантты компоненттері бас осьтен алынғандығын көрсетеді. 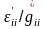және 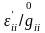қатынастары сәйкес мынаған тең болады , 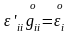және

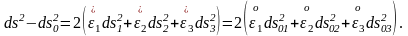
Сондай-ақ, қозғалатын ортаның әрбір нүктесін деформация тензорының бас осінің бойымен бағытталған әдеттегі ортогональді декарт координаталар жүйесімен 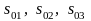байланыстыруға болады, сонда қозғалыс процесінде тағыда дағдылы ортогональ декарт координаталар жүйесіне 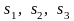көшеді. Бұл жүйедегі деформация тензорына сәйкес 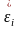және 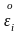тензорлар компоненттері әртүрлі басты компоненттер болып табылады. Жалпы жағдайда  , бірақ олардың арасында белгілі бір байланыс бар.

Бас бағыттарға қатысты мынаны аламыз

,

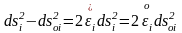бұдан мынадай екі теңдікке келеміз

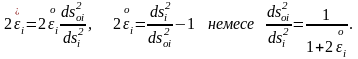
Енді төмендегі теңдіктер орынды болғандықтан

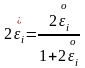, ал (1)

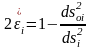өрнектен

,

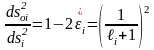бұдан салыстырмалы ұзару коэффициенттері үшін мынадай өрнекті алуға болады, яғни

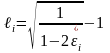немесе (1) ескеріп

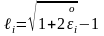. (2)

Шексіз аз деформация жағдайында 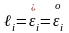бас осьтің бойымен бағытталған салыстырмалы ұзару коэффициенті «бастапқы күйдегі» және актуаль кеңістіктегі деформация тензорының бас компоненттерімен дәл келеді.

Мынадай матрицаны алайық мұндағы 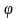- белгілі бір сандық параметр және оны да матрица деп түсінеміз

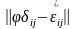, сол сияқты .

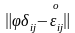Бас осьтегі матрицаның түрі

.

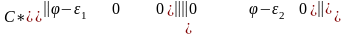Егер детерминантты алып оны нольге теңестірсек, -ға қатысты кубтық теңдеуді аламыз

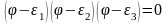
немесе

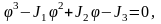
мұндағы

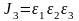
деформация тензорының бірінші, екінші, үшінші инварианттары. Бұл теңдеудің 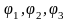түбірлері деформация тензорының сәйкес бас компоненттері болып табылады.

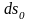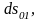
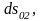
және сызықтық элементтердің актуальді және «бастапқы» күйлердегі сәйкестігін зерттегеннен кейін, осы күйлердегі элементар көлемдердің сәйкестігін табамыз. Деформация тензорының бас осінен бастапқы күйдегі қабырғалары 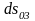, көлемі 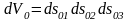формуласымен анықталатын элементар тік бұрышты параллелепипедті алайық. Оның қозғалысына тік бұрышты параллелепипедтің көлемі сәйкес келеді

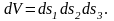
Көлемнің салыстырмалы өзгерісінің шамасын 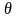көлемдік ұлғаю коэффициенті деп атайды

.

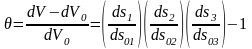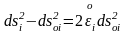болғандықтан, -ны басқаша түрде жазуға болады

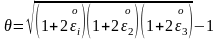(3)

немесе

.

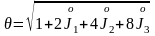Сонымен шамасы инвариантты геометриялық характеристика. Шексіз аз деформация кезінде

. (4)