Математическое программирование

1. Базисные и опорные решения системы линейных уравнений.

2. Постановка задачи линейного программирования (ЗЛП), различные формы записи ЗЛП.

3. Графический метод решения задачи линейного программирования.

4. Симплексный метод решения задачи линейного программирования.

5. Двойственность в линейном программировании. Правила построения двойственной задачи.

6. Основные теоремы двойственности.

7. Постановка и математическая модель транспортной задачи (ТЗ).

8. Открытая и закрытая модели транспортной задачи.

9. Методы северо-западного угла и минимального элемента построения плана ТЗ.

10. Метод потенциалов решения ТЗ.

11. Сетевой график комплекса операций. Временные параметры сетевого графика.

12. Основные понятия теории игр: стратегия игрока, платёжная матрица, седловая точка матричной игры, упрощение матричной игры.

13. Сведение матричной игры к ЗЛП.

14. Статистические игры. Критерии Байеса, Лапласа, Вальда, Сэвиджа, Гурвица решения статистических игр.

15. Задачи нелинейного программирования (ЗНП). Метод множителей Лагранжа.

16. Понятие о градиентных методах решения ЗНП.

17. Элементы финансово - экономических расчетов. Простые проценты. Сложные проценты. Формулы наращения.

Задачи для самостоятельного выполнения

ЗЛП решить графически:

1. 

2. 

3. 

4. 

5. 

ЗЛП решить симплекс-методом:

1. (здесь - номер студента по списку)

Для приведённых ЗЛП написать двойственную:

3. 

4. 

5. 

Составить первоначальный план ТЗ методом северо-западного угла и(или) методом минимального элемента по следующим данным:

1

		1	2	3
		65	158	63
1	175	7	2	3
2	37	4	7	5
3	195	6	5	6

2

		1	2	3
		48	144	175
1	68	3	5	7
2	34	7	5	3
3	141	1	2	3

3

		1		2
		140		184
1	67		3		7
2	48		6		3
3	88		6		3
4	175		4		4

Образцы решения задач

ПРИМЕР 10. Решить задачу линейного программирования графическим методом:

max(min) Z = 3x₁ + 2x₂,

_{x1 ≥ 0, x2 ≥ 0.}

Решение. Построим область допустимых решений Ω. Из теории следует, что это будет выпуклое множество. Для этого запишем уравнения границ области допустимых решений. Заменив в ограничениях знак неравенства знаком равенства

x₁ + 2x₂, = 14, (I)

x₁ – 4x₂, = – 22, (II)

x₁ – x₂, = 2, (III)

построим эти прямые.

Определим полуплоскости, удовлетворяющие неравенствам ограничениям. Пересечение этих полуплоскостей образует треугольник АВС, который и является областью допустимых решений Ω. Покажем ее на рисунке 2 штриховкой.

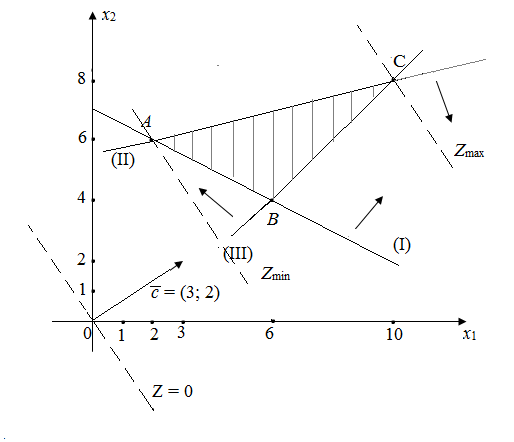
Рисунок 3 – Область допустимых решений Ω

Строим вектор  = (3; 2) – градиент целевой функции Z(х₁; х₂).

Далее проводим линию нулевого уровня 3x₁ + 2x₂, = 0, перпендикулярную вектору  = (3; 2).

Перемещаем линию нулевого уровня в направлении вектора . Первой точкой контакта линии уровня с треугольником АВС является точка А и, следовательно, Z_min = Z(А). Последняя точка контакта – точка С, и следовательно, Z_max = Z(C).

Найдем координаты точек A и С и вычислим экстремальные значения целевой функции.

Точка A – точка пересечения прямых (I) и (II).

А(2; 6), Z_min = Z(А) = Z(2; 6) = 3·2 + 2·6 = 18.

Точка С – точка пересечения прямых (II) и (III).

С(10; 8), Z_max = Z(C) = Z(10; 8) = 3·10 + 2·8 = 46.

Ответ: Z_min = 18, Z_max = 46.

Алгоритм симплексных преобразований (перехода к нехудшему опорному плану)

Рассматривается задача линейного программирования на максимум. Приводим ее к каноническому виду и заносим в симплексную таблицу. Если все , то начальный опорный план оптимален. Если же существуют , то план неоптимален и его нужно улучшить. Среди отрицательных оценок находим максимальную по абсолютной величине:

.

Столбец называется разрешающим.

(Если задача решается на минимум, то разрешающий столбец выбирается из условия ).

Переменную , соответствующую разрешающему столбцу, следует ввести в базис. Для определения переменной, выводимой из базиса, находят отношения для i, у которых (они называются симплексными).

Среди симплексных отношений определяют наименьшее, т.е.

=  = Θ.

Оно и укажет строку, в которой содержится исключаемая из базиса переменная . Строка , соответствующая минимальному симплексному отношению, называется разрешающей. Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки, также называется разрешающим. Чтобы завершить шаг преобразований, ведущий к новому опорному плану, составляем новую симплексную таблицу по следующим правилам:

1. Элементы строки новой таблицы равны соответствующим элементам разрешающей строки старой таблицы, делённым на разрешающий элемент.

2. Все элементы столбца новой таблицы равны нулю, за исключением

= 1/

3. Чтобы получить все остальные элементы (включая элементы индексной строки) новой таблицы, надо из соответствующего элемента прежней таблицы вычесть произведение элемента разрешающей строки на элемент разрешающего столбца, разделенное на разрешающий элемент:

– – – –

׀ ׀

׀ ׀

׀ ׀

– – – – ,

= = .

Для контроля вычислений элементов индексной строки применяют формулы:

, .

ПРИМЕР 11. На предприятии выпускается четыре вида продукции П_j . Для ее изготовления используются три вида ресурсов Р_i ( . Ресурсы ограничены величинами . Расход ресурса i-го вида на единицу продукции j-го вида составляет единиц. Цена за единицу продукции j-го вида равна с_j единиц. Все данные приведены в таблице 7.

Таблица 7

	П1	П2	П3	П4	bi
Р1	3	1	2	2	90
Р2	2	3	4	5	80
Р3	3	6	4	3	100
cj	10	12	14	12	Z

Требуется:

1) составить экономико-математическую модель задачи, пользуясь которой, можно найти план выпуска продукции, при котором общая прибыль будет наибольшей;

2) симплексным методом найти оптимальный план выпуска продукции и максимальную величину прибыли;

3) составить задачу двойственную к исходной, и пояснить ее экономическую суть. Используя теорию двойственности, установить соответствие между переменными прямой и двойственной задач, найти двойственные оценки;

4) с помощью двойственных оценок исследовать:

а) степень полезности отдельных видов ресурсов в условиях производства;

б) величину финансовых потерь в расчете на единицу продукции в случае, если предприятие вынуждено будет производить невыгодные ему виды продукции. При необходимости такого производства обосновать цены на готовую продукцию.

Решение. 1) Составим экономико-математическую модель задачи. Обозначим через х₁, х₂, х_3, х₄ количество весовых единиц четырех видов продукции, которые планируется изготовить. Тогда суммарная прибыль, полученная от реализации выпущенной продукции, будет равна:

.

Переменные х₁, х₂, х₃, х₄ должны удовлетворять ограничениям, накладываемым на расход имеющихся в распоряжении предприятия ресурсов сырья. Эти ограничения выражаются неравенствами:

По смыслу задачи

Итак, математическая модель задачи имеет вид:

Перейдем к канонической форме задачи линейного программирования, введя дополнительные (балансовые) переменные х₅, х₆, х₇, означающие возможные остатки ресурсов сырья:

.

Система ограничений в построенной задаче имеет предпочтительный вид, так как правые части неотрицательные, а левые части каждого равенства содержат переменные с коэффициентом равным единице. Эти переменные называются базисными переменными. В целевую функцию дополнительные переменные входят с коэффициентом, равным нулю. Переменные называются свободными, их значения принимаются равными нулю. Тогда значения базисных переменных будут равны: . Запишем начальный опорный план задачи .

2) Peшим полученную задачу линейного программирования симплексным методом. Составим начальную симплексную таблицу 8.

Таблица 8

БП	СБ		Ао		х1	х2		х3		х4		х5		х6		х7		Θ
					10	12		14		12		0		0		0
х5	0		90		3	1		2		2		1		0		0		45
х6	0		80		2	3		4		5		0		1		0		20
х7	0		100		3	6		4		3		0		0		1		25
Zj – Cj		0		–10		–12	–14		–12		0		0		0

Полученный план (0,0,0,0,90,80,100) является опорным, но не является оптимальным, так как в индексной строке Z_j – C_j все оценки неположительные. Наибольший по модулю отрицательный элемент (– 14) индексной строки указывает, что в новый базис следует ввести переменную х₃. Столбец, соответствующий выбранной переменной, называется разрешающим столбцом. Чтобы определить переменную, выводимую из базиса, составляем симплексные отношения. Для этого нужно элементы столбца А₀ разделить на соответствующие элементы разрешающего столбца и выбрать наименьшее из них:

,

следовательно, из базиса нужно вывести переменную х₆.

Переходим к новому опорному плану, выполнив симплексные преобразования. Вычисления заносим в таблицу 9.

Таблица 9

БП	СБ	Ао	х1	х2	х3	х4	х5	х6	х7	Θ
			10	12	14	12	0	0	0
х5	0	50	2	– 0,5	0	– 0,5	1	– 0,5	0	25
х3	14	20	0,5	0,75	1	1,25	0	0,25	0	40
х7	0	20	1	3	0	– 2	0	– 1	1	20
Zj – Cj		280	– 3	– 1,5	0	5,5	0	3,5	0

План (0; 0; 20; 0; 50; 0; 20) не является оптимальным так, как есть отрицательные индексные оценки, и поэтому переходим к следующему нехудшему опорному плану. Введем в базис х₁, выведем – х₇. Переход к новому опорному плану выполним в таблице 10.

Таблица 10

БП	СБ	Ао	х1	х2	х3	х4	х5	х6	х7	Θ
			10	12	14	12	0	0	0
х5	0	10	0	– 6,5	0	3,5	1	1,5	– 2	2,86
х3	14	10	0	– 0,75	1	2,25	0	0,75	– 0,5	4,44
х1	10	20	1	3	0	– 2	0	– 1	1	–
Zj – Cj		340	0	7,5	0	– 0,5	0	0,5	3

Полученный план (20; 0; 10; 0; 10; 0; 0) не является оптимальным так, как есть отрицательные индексные оценки, и поэтому переходим к следующему нехудшему опорному плану. Введем в базис х₄, выведем – х₅. Переход к новому опорному плану выполним в таблице 11.

Таблица 11

БП	СБ	Ао	х1	х2	х3	х4	х5	х6	х7	Θ
			10	12	14	12	0	0	0
х4	12	2,86	0	– 1,86	0	1	0,29	0,43	– 0,57
х3	14	3,57	0	3,43	1	0	– 0,64	– 0,21	0,79
х1	10	25,71	1	– 0,71	0	0	0,57	– 0,14	– 0,14
Zj – Cj		341,4	0	6,57	0	0	0,14	0,71	2,71

Так как в индексной строке нет отрицательных оценок, то план (25,71; 0; 3,57; 2,86; 0; 0; 0) является оптимальным. Он является единственным, так как все свободные переменные имеют оценки, отличные от нуля.

Максимальная прибыль предприятия составит 341,43 денежные единицы, если оно выпустит 25,71 весовых единиц продукции первого вида, 3,57 весовых единиц третьего вида и 2,86 весовых единиц продукции четвертого вида, а продукцию второго вида вообще выпускать не будет. Так как , то все виды ресурсов при выполнении оптимального плана будут израсходованы полностью.

3) Составим модель двойственной задачи. Обозначим через у_i ≥ 0 цену единицы сырья i-го вида. Модель двойственной задачи имеет вид

;

Из первой теоремы двойственности следует, что если решена одна из пары двойственных задач, то одновременно найдено решение и другой задачи. Компоненты оптимального плана двойственной задачи находятся в индексной строке последней симплексной таблицы уже решенной задачи. Запишем каноническую форму математической модели двойственной задачи, введя дополнительные (балансовые) переменные

;

.

Между переменными двойственных задач устанавливается соответствие

Учитывая это соответствие, выписываем из индексной строки последней симплексной таблицы двойственные оценки. Эти оценки являются компонентами оптимального плана двойственной задачи. Запишем оптимальный план двойственной задачи

 = (0,14; 0,71; 2,71; 0; 6,57; 0; 0).

4) Оценки для первого, второго и третьего видов сырья положительные, что указывает, что эти виды сырья наиболее дефицитные и используются полностью. Увеличение объема сырья первого вида на одну весовую единицу позволило бы получить оптимальный план, для которого доход увеличился бы на 0,14 денежные единицы. Увеличение объема сырья второго и третьего вида на одну весовую единицу позволило бы получить оптимальный план, для которого доход увеличился бы на 0,71 и 2,71 ден. единицы соответственно.

Дополнительные двойственные переменные являются мерой убыточности продукции, которую согласно оптимальному плану нецелесообразно выпускать. Так как  = 6,75, то это говорит о том, что стоимость ресурсов, расходуемых на производство одной единицы продукции второго вида (в прикидочных ценах), превышает стоимость единицы этой продукции (с₂ = 12) на 6,75 ден.ед. Следовательно, в случае необходимости ее производства для рентабельности предприятия, цена на нее должна быть не менее 18,75 ден.ед.

ПРИМЕР 12. Имеется три поставщика и четыре потребителя некоторой продукции. Количество груза а_i, которое может отгрузить поставщик , стоимость (тариф) перевозки из пункта i в пункт j единицы груза c_ij, и потребности потребителей в грузе b_j, j =  , заданы в таблице 12.

Таблица 12

Поставщики и их возможности		Потребители и их потребности
		100		60	150	40
	80	2	5		2	1
	160	4	1		4	2
	110	3	6		3	4

Составить экономико-математическую модель задачи и найти методом потенциалов оптимальный план перевозки груза, при котором общие транспортные затраты будут наименьшими.

Решение. Строим математическую модель задачи. Через х_ij обозначим объем продукции, доставленный от поставщика A_i (i = l,2,3) потребителю B_j ( ). Отметим, что в данном случае сумма количества продукции, которую могут отгрузить все поставщики, совпадает с суммой потребностей потребителей:

100 + 60 + 150+40 = 80 + 160 + 110 = 350.

Значит, задача закрытого типа и имеет решение. Математическая модель задачи принимает вид:

.

Строим начальный опорный план методом «минимального элемента». Распределение груза начинаем с клетки с наименьшим тарифом. Это распределение представлено в таблице 13.

Таблица 13

Bj Ai	В1	В2	Вз	В4	аi
А1	2 + 40	5	2	1 – 40	80	0
А2	4	1 60	4 – 100	2 * +	160	2
A3	3 – 60	6	3 + 50	4	110	1
	100	60	150	40	350
	2	–1	2	1

Число занятых клеток удовлетворяет условию m + n – 1 = 3 + 4 – 1 = 6. Из занятых клеток не образуется замкнутый цикл. Следовательно, план будет опорным. Построенному опорному решению отвечают затраты:

Z₁ = 40∙2 + 40∙1 + 60∙1 + 100∙4 + 60∙3 + 50∙3 = 910.

Проверим полученный опорный план на оптимальность. Для этого i-ой строке и j-ому столбцу ставим в соответствие числа u_i и v_j (потенциалы). Для каждой базисной переменной x_ij потенциалы должны удовлетворять условию u_i + v_j = c_ij. Получаем систему:

u₁ + v₁ = 2, u₁ + v₄ = l, u₂ + v₂ = 1, u₂ + v₃ = 4, u₃ + v₁ = 3, u₃ + v₃ = 3.

Так как система состоит из 6 уравнений, а неизвестных 7,то, чтобы, найти численное решение этой системы, одно из неизвестных зададим произвольно, тогда остальные переменные найдутся из системы однозначно.

Пусть U₁ = 0, тогда v₁ = 2, v₄ = 1, v₂ = – 1, v₃ = 2, u₂ = 2, u₃ = 1.

Теперь для небазисных переменных (свободных клеток) найдем оценки

Sij = cij – (ui + vj):
S12 = 5 – (0 – 1) = 6	S24 = 2 – (1 +2) = – 1 < 0
S13 = 2 – (2 + 0 ) = 0	S32 = 6 – (1 – 1) = 6
S21 = 4 – (2 + 2) = 0	S34 = 4 – (1 +1) = 2

Согласно критерию оптимальности опорного плана (все оценки S_ij неотрицательные) делаем вывод, что построенный план не оптимален, так как среди оценок есть отрицательные.

В базис введем перспективную переменную х₂₄ (отвечающую наибольшей по модулю отрицательной оценке) и строим замкнутый цикл с вершинами в загруженных клетках. Присваиваем клеткам в вершинах цикла поочередно по часовой стрелке знаки "+" и "–", начиная с клетки (2,4), которой присваиваем знак "+".

Выбираем наименьшее значение из клеток со знаком "–", а именно, min (40, 60, 100) = 40 и перераспределим продукцию вдоль замкнутого цикла: прибавляя 40 к значениям в клетках со знаком "+" и вычитая из значений в клетках со знаком "–". В результате приходим к таблице 14

Таблица 14

Bj Ai	В1	В2	Вз	В4	аi	ui
А1	2 80	5	2	1	80	– 2
А2	4	1 60	4 60	2 40	160	0
A3	3 20	6	3 90	4	110	– 1
	100	60	150	40	350
	4	1	4	2

Полученному решению отвечают затраты:

Z₂ = 80∙2 + 60∙1 + 60∙4 +40∙2 + 20∙3 + 90∙3 = 870.

Проверяем полученный план на оптимальность. Для каждой базисной переменной x_ij составим систему уравнений для определения потенциалов:

u₁ + v₁ = 2, u₂ + v₂ = 1, u₂ + v₃ = 4, u₂ + v₄ = 2, u₃ + v₁ = 3, u₃ + v₃ = 3,

Пусть u₂ = 0, тогда v₂ = 1, v₃ = 4, v₄  = 2, u₁ = – 2, u₃ = – 1, v₁ = 4.

Теперь для небазисных переменных найдем оценки

S12 =  5 – (1 – 2) = 6	S14 = 1 – (2 – 2) = 1
S13 = 2 – (4 – 2 ) = 0	S32 = 6  – (1 – 1) = 6
S21 = 4 – (4 + 0) = 0	S34 = 4 – (2 – 1) = 4

Все оценки свободных клеток неотрицательны, следовательно, план

является оптимальным. По этому плану перевозок поставщик А₁ отправляет 80 ед. продукции потребителю В₁ , поставщик А₂ – 60 ед. потребителю В₂, 60 ед. потребителю B₃ и 40 ед. потребителю В₄; поставщик A₃ – 20 ед. потребителю B₁ и 90 ед. потребителю В₃.

Полученному решению отвечают минимальные затраты:

Z₂ = 80∙2 + 60∙1 + 60∙4 + 40∙2 + 20∙3 + 90∙3 = 870.

ПРИМЕР 13. Банк может приобрести на сумму b = 16 денежных единиц акции компании A₁ номинальной стоимости a₁ = 6 денежных единиц, компании A₂ номинальной стоимости a₂ = 5 денежных единиц, компании A₃ номинальной стоимости a₃ = 5 денежных единиц. На конец года рынок ценных бумаг может оказаться в одном из двух состояний: R₁ и R₂.

Специалисты установили, что дивиденды компании A_i для состояния рынка R_j на конец года составят d_ij % от номинальной стоимости ( ): d₁₁= 10; d₁₂= 12; d₂₁= 14; d₂₂= 11; d₃₁= 10; d₃₂= 12.

Требуется:

1) придать описанной ситуации игровую схему, установить характер игры и определить игроков, указав их возможные стратегии;

2) составить платежную матрицу;

3) сформировать портфель акций банка, обеспечивающий как можно большую прибыль.

Учитывать следующие предположения:

а) известны вероятности p₁ и p₂ состояния рынка R₁ и R₂ на конец года;

б) о вероятностях состояния рынка R₁ и R₂ на конец года ничего определенного сказать нельзя.

Указания

1) Оптимальные чистые стратегии следует находить, используя: в п. 3, а) критерий Байеса; в п. 3, б) критерий Лапласа, Вальда, Сэвиджа, Гурвица (величину параметра в критерии Гурвица принимать равной 0,8).

2) Рассмотреть четыре возможные чистые стратегии правления банка.

Решение. 1. В качестве статистика выступает правление банка, которое может принять одно из следующих решений:

– приобрести по одной акции каждой компании (6 + 5 + 5 = 16) – стратегия A₁,

– приобрести одну акцию первой компании и две акции второй (6 + 2∙5 = 16) –стратегия A₂;

– приобрести одну акцию первой компании и две акции третьей (6 + 2∙5 = 16) – стратегия A₃;

– приобрести одну акцию второй компании и две акции третьей (5 + 2∙5 = 15 < 16) – стратегия A₄.

(В указании к условию задачи рекомендуется число способов формирования портфеля акций ограничить четырьмя).

Второй играющей стороной – природой – является возможное состояние рынка ценных бумаг на конец года, которое может быть R₁ и R₂.

Итак, описанная ситуация представляет статистическую игру.

2. Рассчитаем элементы платежной матрицы.

Так, в ситуации (A₁, R₁) элемент а₁₁ вычисляется следующим образом: от одной акции компании A₁ банк получит прибыль 6 0,10 = 0,6 денежных единиц, от одной акции компании А₂ – 5 0,14 = 0,7 денежных единиц и одной акции компании А₃ – 5 0,1=0,5 денежных единиц; в итоге суммарная прибыль банка при его стратегии A₁ и состоянии рынка ценных бумаг в конце года R₁ составит а₁₁ = 0,6 + 0,7 + 0,5 = 1,8. Аналогично определяются и другие элементы платежной матрицы.

Таблица 15

Количество приобретенных акций	Стратегия статистика Ai	Состояние рынка
		R1	R2
1–A1 1–А2 1–А3	A1	1,8	1,87
1–A1 2–А2	A2	2	1,82
1–А1 2–А3	A3	1,6	1,92
1–А2 2–А3	A4	1,7	1,75
	pj	0,6	0,4

3. а) В качестве оптимальной по критерию Байеса, принимается чистая стратегия A₁, при которой максимизируется средняя прибыль т. е. обеспечивается

, ( ).

= 1,8∙0,6 + 1,87∙0,4 = l,828,

= 2∙0,6 + 1,82∙0,4 = 1,928,

= 1,6∙0,6 + 1,92∙0,4 = 1,728,

= 1,7∙0,6 + 1,75∙0,4 = 1,72,

= max{1,828; 1,928; 1,728; 1,72} = 1,928.

Следовательно, правление банка должно приобрести одну акцию компании A₁ и две акции А₂ .

б) Пусть вероятности состояния рынка R₁ и R₂ на конец года равны, т. е. p₁ = p₂ = 0,5. Тогда можно воспользоваться критерием Лапласа, в соответствии с которым оптимальной считается стратегия, обеспечивающая

= max .

= 0,5∙(1,8 + 1,87) = 1,835;

= 0,5∙ (2 + 1,82) = 1,91;

= 0,5∙(1,6 + 1,92) = 1,76;

= 0,5∙(1,7 +1,75) = 1,725;

= mах {1,835; 1,91; 1,76; 1,725} = 1,91.

Следовательно, опять в качестве оптимальной надо взять чистую стратегию A₂, т.е. правление банка должно приобрести одну акцию компании A₁ и две акции компании A₂.

в) Пусть о вероятностях состояния рынка ценных бумаг R₁ и R₂ на конец года ничего определенного сказать нельзя. В этом случае можно воспользоваться критериями Вальда, Сэвиджа и Гурвица.

Максиминный критерий Вальда. Это критерий крайнего пессимизма. В соответствии с этим критерием в качестве оптимальной рекомендуется выбирать ту стратегию, которая гарантирует в наихудших условиях максимальный выигрыш, т. е. максиминную стратегию.

= max min = max , = min ,

i j i j

=1,8; =l,82; =l,6; =l,7;

= max = max (l,8; 1,82; 1,6; 1,7) = 1,82 = .

i

Следовательно, по критерию Вальда оптимальной является также чистая стратегия A₂ (необходимо приобрести одну акцию A₁ и две акции компании А₃).

Критерий Сэвиджа (минимаксного риска). Этот критерий, так же как и критерий Вальда, является критерием крайнего пессимизма. Согласно этому критерию рекомендуется выбирать ту стратегию, при которой в наихудших условиях величина риска принимает наименьшее значение.

= min max .

i j

Построим матрицу рисков , где , где – максимально возможный выигрыш статистика при состоянии R_j (максимальный элемент j-ого столбца платежной матрицы), т. е. = max .

Таблица 16

	R1	R2	max j
A1	0,2	0,05	0,2
A2	0	0,1	0,1
A3	0,4	0	0,4
A4	0,3	0,17	03

=min max =min {0,2; 0,1; 0,4; 0,3} = 0,1.

i j

Следовательно, и по критерию Сэвиджа оптимальной будет чистая стратегия A₂.

Критерий Гурвица. Этот критерий называют критерием обобщенного максимума или пессимизма-оптимизма, он имеет вид:

S=max{ min + (1 – ) mах } = mах ,

i j j i

где : 0 1; в нашем случае = 0,8. Все промежуточные вычисления будем проводить в таблице 17:

Таблица 17

	R1	R2	min j	0,8min j	mах j	0,2 mах j	hi
A1	1,8	1,87	1,8	1,44	1,87	0,37	1,81
A2	2	1,82	1,82	1,46	2	0,4	1,86
A3	1,6	1,92	1,6	1,28	1,92	0,38	1,66
A4	1,7	1,75	1,7	1,36	1,75	0,35	1,71

max h_i = max {1,81; 1,86; 1,66; 1,71} = 1,86.

i

Следовательно, по критерию Гурвица оптимальной чистой стратегией является стратегия A₂ (т. е. наибольшую прибыль получит банк, если правление банка приобретет одну акцию компании A₁ и две акции компании А₂).

Замечание. В платежной матрице (таблица 15) стратегия A₄ является доминируемой по отношению к другим стратегиям, поэтому её можно было сразу исключить из рассмотрения.