Алгоритм симплексных преобразований (перехода к нехудшему опорному плану)

Рассматривается задача линейного программирования на максимум. Приводим ее к каноническому виду и заносим в симплексную таблицу. Если все , то начальный опорный план оптимален. Если же существуют , то план неоптимален и его нужно улучшить. Среди отрицательных оценок находим максимальную по абсолютной величине:

.

Столбец называется разрешающим.

(Если задача решается на минимум, то разрешающий столбец выбирается из условия ).

Переменную , соответствующую разрешающему столбцу, следует ввести в базис. Для определения переменной, выводимой из базиса, находят отношения для i, у которых (они называются симплексными).

Среди симплексных отношений определяют наименьшее, т.е.

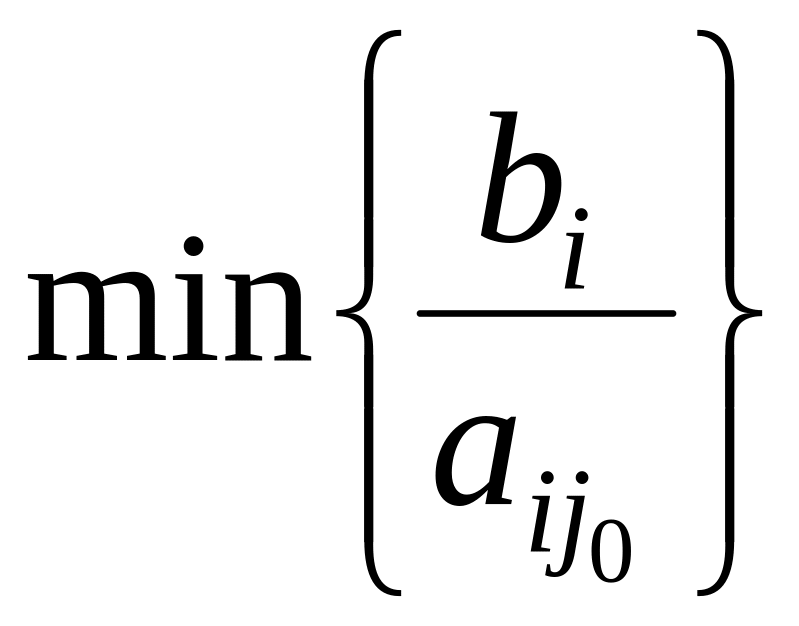=  = Θ.

Оно и укажет строку, в которой содержится исключаемая из базиса переменная . Строка , соответствующая минимальному симплексному отношению, называется разрешающей. Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки, также называется разрешающим. Чтобы завершить шаг преобразований, ведущий к новому опорному плану, составляем новую симплексную таблицу по следующим правилам:

1. Элементы строки новой таблицы равны соответствующим элементам разрешающей строки старой таблицы, делённым на разрешающий элемент.

2. Все элементы столбца новой таблицы равны нулю, за исключением

= 1/

3. Чтобы получить все остальные элементы (включая элементы индексной строки) новой таблицы, надо из соответствующего элемента прежней таблицы вычесть произведение элемента разрешающей строки на элемент разрешающего столбца, разделенное на разрешающий элемент:

– – – –

׀ ׀

׀ ׀

׀ ׀

– – – – ,

= = .

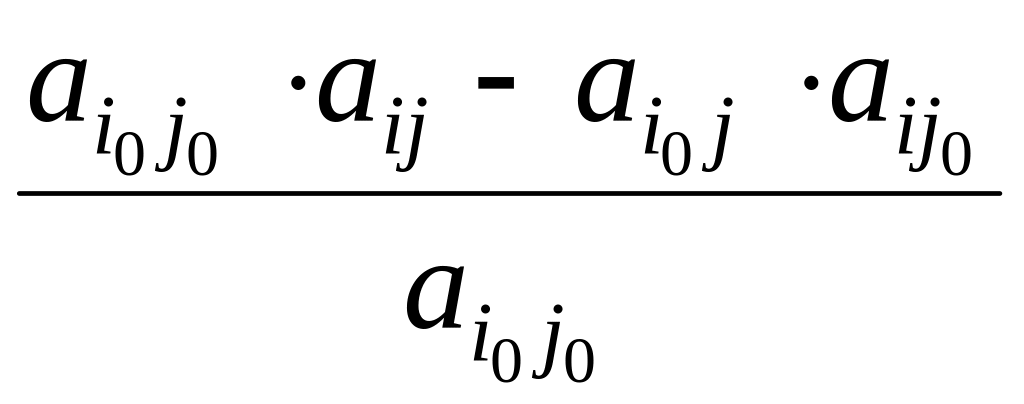Для контроля вычислений элементов индексной строки применяют формулы:

, .

ПРИМЕР 7. На предприятии выпускается четыре вида продукции П_j . Для ее изготовления используются три вида ресурсов Р_i ( . Ресурсы ограничены величинами . Расход ресурса i-го вида на единицу продукции j-го вида составляет единиц. Цена за единицу продукции j-го вида равна с_j единиц. Все данные приведены в таблице 7.

Таблица 7

	П1	П2	П3	П4	bi
Р1	3	1	2	2	90
Р2	2	3	4	5	80
Р3	3	6	4	3	100
cj	10	12	14	12	Z

Требуется:

1) составить экономико-математическую модель задачи, пользуясь которой, можно найти план выпуска продукции, при котором общая прибыль будет наибольшей;

2) симплексным методом найти оптимальный план выпуска продукции и максимальную величину прибыли;

3) составить задачу двойственную к исходной, и пояснить ее экономическую суть. Используя теорию двойственности, установить соответствие между переменными прямой и двойственной задач, найти двойственные оценки;

4) с помощью двойственных оценок исследовать:

а) степень полезности отдельных видов ресурсов в условиях производства;

б) величину финансовых потерь в расчете на единицу продукции в случае, если предприятие вынуждено будет производить невыгодные ему виды продукции. При необходимости такого производства обосновать цены на готовую продукцию.

Решение. 1) Составим экономико-математическую модель задачи. Обозначим через х₁, х₂, х_3, х₄ количество весовых единиц четырех видов продукции, которые планируется изготовить. Тогда суммарная прибыль, полученная от реализации выпущенной продукции, будет равна:

.

Переменные х₁, х₂, х₃, х₄ должны удовлетворять ограничениям, накладываемым на расход имеющихся в распоряжении предприятия ресурсов сырья. Эти ограничения выражаются неравенствами:

По смыслу задачи

Итак, математическая модель задачи имеет вид:

Перейдем к канонической форме задачи линейного программирования, введя дополнительные (балансовые) переменные х₅, х₆, х₇, означающие возможные остатки ресурсов сырья:

.

Система ограничений в построенной задаче имеет предпочтительный вид, так как правые части неотрицательные, а левые части каждого равенства содержат переменные с коэффициентом равным единице. Эти переменные называются базисными переменными. В целевую функцию дополнительные переменные входят с коэффициентом, равным нулю. Переменные называются свободными, их значения принимаются равными нулю. Тогда значения базисных переменных будут равны: . Запишем начальный опорный план задачи .