Задания контрольной работы для студентов специальности эппЗс (5 семестр)
ЗАДАНИЕ 1. Из N акционерных обществ (АО) n являются банкротами. Гражданин приобрел по одной акции каждого из m АО. Какова вероятность того, что среди m купленных акций k окажутся акциями, купленными у АО банкротов?
Значения параметров к условию задания 5 приведены в таблице 5.
Таблица 1
№ вар. |
N |
n |
m |
k |
|
№ вар. |
N |
n |
m |
k |
1 |
20 |
4 |
6 |
2 |
|
2 |
25 |
5 |
4 |
2 |
3 |
20 |
3 |
7 |
2 |
|
4 |
30 |
4 |
8 |
3 |
5 |
30 |
5 |
6 |
3 |
|
6 |
27 |
4 |
5 |
2 |
7 |
30 |
4 |
7 |
2 |
|
8 |
24 |
5 |
7 |
2 |
9 |
26 |
4 |
5 |
3 |
|
10 |
34 |
4 |
8 |
2 |
11 |
24 |
5 |
6 |
2 |
|
12 |
35 |
4 |
7 |
3 |
13 |
28 |
5 |
4 |
2 |
|
14 |
24 |
3 |
6 |
2 |
ЗАДАНИЕ
2. В
некотором городе имеется N
коммерческих
банков, оценка надежности которых равна
.
В связи с определением хозяйственных
перспектив развития города администрацию
интересует вероятность того, что в
течение года обанкротятся (см. таблицу
5):
Таблица 2
№ вар. |
|
1 |
N=3, p1=0,9, p2=0,95, p3=0,8 а) два банка; б) не более одного банка; в) только один банк |
2 |
N=3, p1=0,85, p2=0,95, p3=0,95 а) три банка; б) хотя бы один банк; в) более одного банка |
3 |
N=4, p1=0,9, p2=0,8, p3=0,75, p4= 0,85 а) не менее трех банков; б) хотя бы один банк; в) два банка |
4 |
N=3, p1=0,85, p2=0,9 , p3=0,93 а) хотя бы один банк; б) два банка; в) только один банк |
5 |
N=3, p1=0,78; p2=0,98; p3=0,95 а) три банка; б) не менее двух банков; в) только один банк |
6 |
N=4, p1=0,85; p2=0,98; p3=0,9; p4=0,8 а) все четыре банка; б) более двух банков; в) только один банк |
Продолжение таблицы 2
№ вар. |
|
7 |
N=3, p1=0,9; p2=0,95; p3=0,89 а) два банка; б) хотя бы один банк; в) один банк |
8 |
N=3, p1=0,95; p2=0,85; p3=0,8 а) более двух банков; б) один банк; в) хотя бы один банк |
9 |
N=4, p1=0,8; p2=0,95; p3=0,9; p4= 0,85 а) два банка; б) хотя бы один банк; в) менее двух банков |
10 |
N=3, p1=0,9; p2=0,85; p3=0,75 а) три банка; б) хотя бы один банк; в) не более двух банков |
11 |
N=4, p1=0,85; p2=0,8; p3=0,9; p4= 0,7 а) два банка; б) хотя бы один банк; в) не менее трех банков |
12 |
N=3, p1=0,95; p2=0,85; p3=0,9 а) хотя бы один банк; б) два банка; в) менее двух банков |
13 |
N=3, p1=0,8; p2=0,9; p3=0,96 а) три банка; б) не менее двух банков; в) не более двух банков |
14 |
N=4, p1=0,95; p2=0,9; p3=0,8; p4= 0,85 а) хотя бы один банк; б) менее двух банков; в) три банка |
ЗАДАНИЕ 3. В новом микрорайоне поставлено п единиц кодовых замков на входных дверях домов. Вероятность того, что в течение года замок не потребует ремонта, равна р. Какова вероятность того, что в течение года не потребуют ремонта:
ровно k замков;
не менее k замков?
Значения параметров к условию задания 7 приведены в таблице 7.
Таблица 3
№ вар. |
п |
р |
k |
|
№ вар. |
п |
р |
k |
1 |
99 |
0,8 |
85 |
|
2 |
128 |
0,9 |
112 |
3 |
112 |
0,9 |
98 |
|
4 |
96 |
0,8 |
90 |
5 |
123 |
0,95 |
120 |
|
6 |
87 |
0,85 |
80 |
7 |
134 |
0,96 |
123 |
|
8 |
92 |
0,93 |
87 |
9 |
128 |
0,98 |
120 |
|
10 |
78 |
0,97 |
70 |
11 |
124 |
0,86 |
118 |
|
12 |
85 |
0,89 |
78 |
13 |
115 |
0,88 |
109 |
|
14 |
132 |
0,95 |
124 |
ЗАДАНИЕ 4. Телевизионный канал рекламирует новый вид детского питания. Вероятность того, что телезритель увидит эту рекламу, равна р. В случайном порядке выбраны k телезрителей. Составьте ряд распределения случайной величины Х — числа телезрителей, видевших рекламу. Найдите:
числовые характеристики этого распределения: М(Х), D(X);
функцию распределения F(X) и постройте ее график;
вероятность того, что:
ни один телезритель не увидит эту рекламу;
хотя бы один телезритель увидит эту рекламу;
не более двух телезрителей увидят эту рекламу.
Значения параметров к условию задания 8 приведены в таблице 8.
Таблица 4
№ вар. |
р |
k |
|
№ вар. |
р |
k |
|
№ вар. |
р |
k |
1 |
0,2 |
5 |
|
2 |
0,4 |
4 |
|
3 |
0,9 |
5 |
4 |
0,5 |
4 |
|
5 |
0,7 |
4 |
|
6 |
0,25 |
5 |
7 |
0,3 |
4 |
|
8 |
0,8 |
5 |
|
9 |
0,25 |
4 |
10 |
0,4 |
5 |
|
11 |
0,7 |
5 |
|
12 |
0,75 |
4 |
13 |
0,6 |
5 |
|
14 |
0,8 |
4 |
|
15 |
0,35 |
4 |
ЗАДАНИЕ
5. Администрацию
универсама интересует оптимальный
уровень запасов продуктов в торговом
зале, а также среднемесячный объем
покупок товаров, не являющихся предметом
ежедневного потребления в семье (таких,
например, как сода). Для выяснения этого
вопроса менеджер универсама в течение
двух месяцев регистрировал частоту
покупок стограммовых пакетиков с содой
и собрал следующие данные (
): – (таблица 9).
Требуется:
составить интервальный статистический ряд распределения значений статистических данных;
построить гистограмму и полигон относительных частот;
найти эмпирическую функцию распределения и построить её график;
вычислить числовые характеристики выборки (выборочную среднюю
,
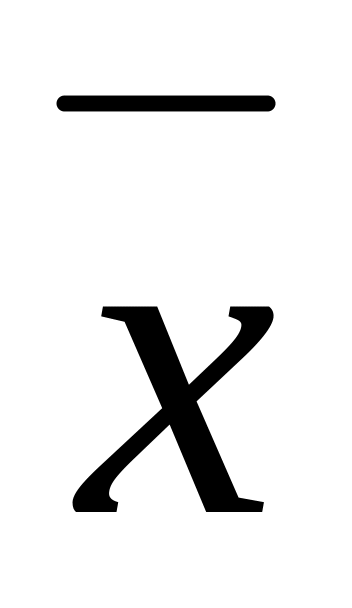выборочное среднее квадратичное
отклонение
).
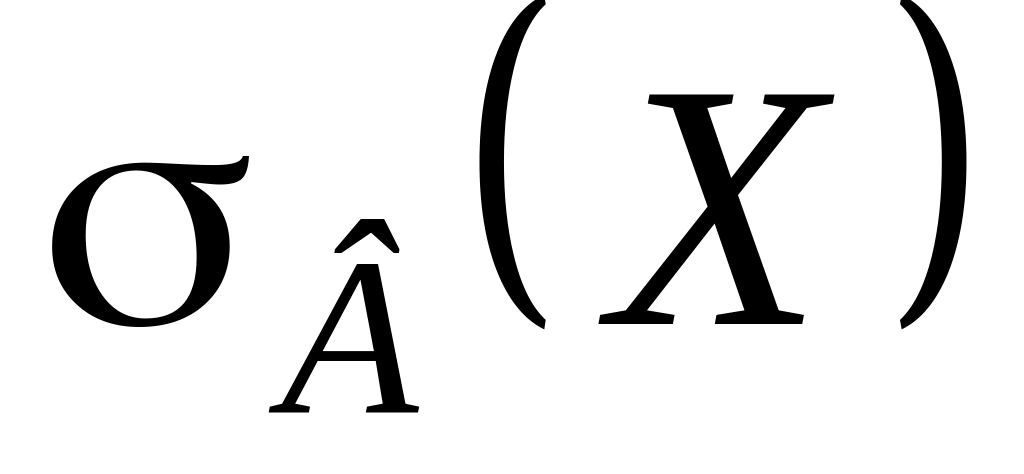Значения параметров к условию задания 9 приведены в таблице 9.
Таблица 5
№№ строк |
Данные
( |
|||||||||
1 |
8 |
4 |
4 |
9 |
3 |
3 |
1 |
2 |
0 |
4 |
2 |
2 |
3 |
5 |
7 |
10 |
6 |
5 |
7 |
3 |
2 |
3 |
9 |
8 |
1 |
4 |
6 |
5 |
4 |
2 |
1 |
0 |
4 |
8 |
5 |
5 |
4 |
7 |
3 |
2 |
9 |
7 |
4 |
5 |
10 |
4 |
5 |
3 |
6 |
6 |
5 |
6 |
4 |
7 |
6 |
7 |
9 |
8 |
5 |
2 |
3 |
6 |
4 |
7 |
8 |
7 |
5 |
6 |
7 |
10 |
3 |
5 |
4 |
3 |
8 |
7 |
8 |
3 |
5 |
6 |
6 |
2 |
9 |
4 |
5 |
7 |
5 |
9 |
4 |
4 |
7 |
4 |
3 |
2 |
3 |
8 |
6 |
4 |
10 |
2 |
2 |
9 |
5 |
8 |
7 |
5 |
7 |
5 |
9 |
)Указание: Рассматривать выборку объёма п = 60. Для каждого конкретного варианта надо выбрать из 10 предложенных строк статистических данных таблицы 9 только 6 строк согласно таблице 10:
Таблица 6
-
№ варианта
№№ строк
№ варианта
№№ строк
1
1,2,3,5,7,4
2
1,2,4,6,8,10
3
1,2,6,5,3,9
4
1,2,5,3,7,9
5
1,3,7,2,8,4
6
1,4,10,2,7,5
7
2,3,8,7,6,9
8
3,4,5,6,8,10
9
3,4,9,1,5,2
10
3,5,7,9,10,2
11
2,4,10,9,8,7
12
1,5,8,6,7,3
13
2,5,6,1,3,10
14
4,5,9,2,3,10
ЗАДАНИЕ 7. Решить задачу линейного программирования графическим методом:
max(min)Z = c1x1 + c2x2,
x1 ≥ 0, x2 ≥ 0.
Задание приведено в таблице11.
Таблица 8
В-т |
|
В-т |
|
В-т |
|
1 |
Z = 2x1 + x2,
|
2 |
Z = x1 + 5x2,
|
3 |
Z = x1 + 5x2,
|
Продолжение таблицы 8
В-т |
|
В-т |
|
В-т |
|
|
4 |
Z = 2x1 + 3x2,
|
5 |
Z = 4x1 + 3x2,
|
6 |
Z = 5x1 + x2,
|
|
7 |
Z = 4x1 + x2,
|
8 |
Z = x1 + 4x2,
|
9 |
Z = x1 + x2,
|
|
10 |
Z = 2x1 + 3x2,
|
11 |
Z = 2x1 + 3x2,
|
12 |
Z = x1 + 2x2,
|
|
13 |
Z = 2x1 + 3x2,
|
14 |
Z = 3x1 + x2,
|
15 |
Z = 2x1 + x2,
|
|
ЗАДАНИЕ
8. На
предприятии выпускается четыре вида
продукции Пj
.
Для ее изготовления используются три
вида ресурсов Рi
(
.
Ресурсы ограничены величинами
.
Расход ресурса i-го
вида на единицу продукции j-го
вида составляет
единиц.
Цена за единицу продукции j-го
вида равна сj
единиц. Все данные приведены в таблице
12.
Таблица 9
|
П1 |
П2 |
П3 |
П4 |
Запасы ресурсов |
Р1 |
|
|
|
|
|
Р2 |
|
|
|
|
|
Р3 |
|
|
|
|
|
сj |
с1 |
с2 |
с3 |
с4 |
|
Требуется:
1) cоставить экономико-математическую модель задачи, пользуясь которой, можно найти план выпуска продукции, при котором общая прибыль Z будет наибольшей;
2) cимплексным методом найти оптимальный план выпуска продукции и максимальную величину прибыли;
3) cоставить задачу, двойственную к исходной, и пояснить ее экономическую суть; используя теорию двойственности, установить соответствие между переменными прямой и двойственной задач, найти двойственные оценки.
4) c помощью двойственных оценок исследовать:
а) степень полезности отдельных видов ресурсов в условиях производства;
б) величину финансовых потерь в расчете на единицу продукции в случае, если предприятие вынуждено будет производить невыгодные ему виды продукции. При необходимости такого производства обосновать цены на готовую продукцию.
Вариант 1 Вариант 2
|
П1 |
П2 |
П3 |
П4 |
bj |
|
|
П1 |
П2 |
П3 |
П4 |
bj |
Р1 |
2 |
2 |
3 |
0 |
20 |
|
Р1 |
2 |
1 |
1 |
3 |
240 |
Р2 |
3 |
1 |
1 |
2 |
37 |
|
Р2 |
1 |
0 |
2 |
1 |
60 |
Р3 |
0 |
1 |
1 |
4 |
30 |
|
Р3 |
1 |
2 |
1 |
0 |
300 |
cj |
11 |
6 |
9 |
2 |
Z |
|
cj |
4 |
2 |
3 |
5 |
Z |
Вариант 3 Вариант 4
|
П1 |
П2 |
П3 |
П4 |
bj |
|
|
П1 |
П2 |
П3 |
П4 |
bj |
Р1 |
2 |
3 |
2 |
0 |
20 |
|
Р1 |
1 |
2 |
1 |
0 |
250 |
Р2 |
3 |
1 |
1 |
2 |
37 |
|
Р2 |
1 |
0 |
1 |
1 |
80 |
Р3 |
0 |
1 |
1 |
4 |
30 |
|
Р3 |
2 |
1 |
1 |
1 |
280 |
cj |
11 |
9 |
6 |
2 |
Z |
|
cj |
4 |
3 |
6 |
7 |
Z |
Вариант 5 Вариант 6
|
П1 |
П2 |
П3 |
П4 |
bj |
|
|
П1 |
П2 |
П3 |
П4 |
bj |
Р1 |
2 |
1 |
1 |
3 |
240 |
|
Р1 |
2 |
0 |
3 |
2 |
20 |
Р2 |
1 |
2 |
1 |
0 |
300 |
|
Р2 |
3 |
2 |
1 |
1 |
37 |
Р3 |
1 |
0 |
2 |
1 |
60 |
|
Р3 |
0 |
4 |
1 |
1 |
30 |
cj |
4 |
2 |
3 |
5 |
Z |
|
cj |
11 |
2 |
9 |
6 |
Z |
Вариант 7 Вариант 8
|
П1 |
П2 |
П3 |
П4 |
bj |
|
|
П1 |
П2 |
П3 |
П4 |
bj |
Р1 |
2 |
2 |
0 |
3 |
20 |
|
Р1 |
1 |
2 |
1 |
0 |
300 |
Р2 |
3 |
1 |
2 |
1 |
37 |
|
Р2 |
1 |
0 |
2 |
1 |
60 |
Р3 |
0 |
1 |
4 |
1 |
30 |
|
Р3 |
2 |
1 |
1 |
3 |
240 |
cj |
11 |
6 |
2 |
9 |
Z |
|
cj |
4 |
2 |
3 |
5 |
Z |
Вариант 9 Вариант 10
|
П1 |
П2 |
П3 |
П4 |
bj |
|
|
П1 |
П2 |
П3 |
П4 |
bj |
Р1 |
2 |
1 |
1 |
1 |
280 |
|
Р1 |
1 |
1 |
1 |
2 |
280 |
Р2 |
1 |
2 |
1 |
0 |
250 |
|
Р2 |
1 |
0 |
1 |
1 |
80 |
Р3 |
1 |
0 |
1 |
1 |
80 |
|
Р3 |
0 |
2 |
1 |
1 |
250 |
cj |
4 |
3 |
6 |
7 |
Z |
|
cj |
7 |
3 |
6 |
4 |
Z |
Вариант 11 Вариант 12
|
П1 |
П2 |
П3 |
П4 |
bj |
|
|
П1 |
П2 |
П3 |
П4 |
bj |
Р1 |
3 |
1 |
1 |
2 |
27 |
|
Р1 |
3 |
1 |
1 |
2 |
240 |
Р2 |
2 |
2 |
3 |
0 |
20 |
|
Р2 |
1 |
0 |
2 |
1 |
60 |
Р3 |
0 |
1 |
1 |
4 |
30 |
|
Р3 |
0 |
2 |
1 |
1 |
300 |
cj |
11 |
6 |
9 |
2 |
Z |
|
cj |
5 |
2 |
3 |
4 |
Z |
Вариант 13 Вариант 14
|
П1 |
П2 |
П3 |
П4 |
bj |
|
|
П1 |
П2 |
П3 |
П4 |
bj |
Р1 |
2 |
1 |
1 |
3 |
240 |
|
Р1 |
2 |
1 |
1 |
1 |
280 |
Р2 |
1 |
2 |
0 |
1 |
60 |
|
Р2 |
1 |
0 |
1 |
1 |
80 |
Р3 |
1 |
1 |
2 |
0 |
300 |
|
Р3 |
1 |
2 |
1 |
0 |
250 |
cj |
4 |
3 |
2 |
5 |
Z |
|
cj |
4 |
3 |
6 |
7 |
Z |
ЗАДАНИЕ
9. Требуется
спланировать перевозку строительного
материала с заводов
к строительным площадкам
в вагонах, используя железнодорожную
сеть. В течение каждого квартала на
четырех площадках требуется соответственно
вагонов в квартал. Возможности заводов
равны
вагонов в квартал соответственно.
Стоимость перегона одного вагона с
завода
на
площадку
составляет
единиц.
Данные к задаче представлены в таблице
13.
Таблица 10
Завод и его возможности |
Потребность строительных площадок |
||||
|
|
|
|
||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Требуется:
1) составить экономико – математическую модель задачи;
2) найти оптимальный план перегона вагонов со станций на строительные площадки, минимизирующий общие затраты.
Вариант 1 Вариант 2
Завод и его возможности |
Потребности строительных площадок |
|
|
Завод и его возможности |
Потребности строительных площадок |
||||||||
В1 |
В2 |
В3 |
В4 |
|
|
В1 |
В2 |
В3 |
В4 |
||||
5 |
12 |
18 |
15 |
|
|
100 |
40 |
90 |
120 |
||||
А1 |
10 |
8 |
3 |
5 |
2 |
|
|
А1 |
180 |
12 |
8 |
6 |
5 |
А2 |
15 |
4 |
1 |
6 |
4 |
|
|
А2 |
60 |
15 |
10 |
7 |
8 |
А3 |
25 |
1 |
9 |
4 |
3 |
|
|
А3 |
110 |
3 |
16 |
20 |
15 |
Вариант 3 Вариант 4
Завод и его возможности |
Потребности строительных площадок |
|
|
Завод и его возможности |
Потребности строительных площадок |
||||||||
В1 |
В2 |
В3 |
В4 |
|
|
В1 |
В2 |
В3 |
В4 |
||||
50 |
45 |
60 |
65 |
|
|
100 |
40 |
90 |
120 |
||||
А1 |
60 |
3 |
1 |
4 |
2 |
|
|
А1 |
60 |
15 |
10 |
7 |
8 |
А2 |
70 |
5 |
2 |
3 |
1 |
|
|
А2 |
180 |
12 |
8 |
6 |
5 |
А3 |
90 |
2 |
4 |
5 |
3 |
|
|
А3 |
110 |
3 |
16 |
20 |
15 |
Вариант 5 Вариант 6
Завод и его возможности |
Потребности строительных площадок |
|
|
Завод и его возможности |
Потребности строительных площадок |
||||||||
В1 |
В2 |
В3 |
В4 |
|
|
В1 |
В2 |
В3 |
В4 |
||||
50 |
45 |
65 |
60 |
|
|
50 |
45 |
60 |
65 |
||||
А1 |
60 |
3 |
1 |
2 |
4 |
|
|
А1 |
70 |
5 |
2 |
3 |
1 |
А2 |
70 |
5 |
2 |
1 |
3 |
|
|
А2 |
60 |
3 |
1 |
4 |
2 |
А3 |
90 |
2 |
4 |
3 |
5 |
|
|
А3 |
90 |
2 |
4 |
5 |
3 |
Вариант 7 Вариант 8
Завод и его возможности |
Потребности строительных площадок |
|
|
Завод и его возможности |
Потребности строительных площадок |
||||||||
В1 |
В2 |
В3 |
В4 |
|
|
В1 |
В2 |
В3 |
В4 |
||||
100 |
40 |
90 |
120 |
|
|
45 |
50 |
60 |
65 |
||||
А1 |
110 |
3 |
16 |
20 |
15 |
|
|
А1 |
60 |
1 |
3 |
4 |
2 |
А2 |
60 |
15 |
10 |
7 |
8 |
|
|
А2 |
70 |
2 |
5 |
3 |
1 |
А3 |
180 |
12 |
8 |
6 |
5 |
|
|
А3 |
90 |
4 |
2 |
5 |
3 |
Вариант 9 Вариант 10
Завод и его возможности |
Потребности строительных площадок |
|
|
Завод и его возможности |
Потребности строительных площадок |
||||||||
В1 |
В2 |
В3 |
В4 |
|
|
В1 |
В2 |
В3 |
В4 |
||||
5 |
12 |
18 |
15 |
|
|
50 |
45 |
60 |
65 |
||||
А1 |
15 |
4 |
1 |
6 |
4 |
|
|
А1 |
90 |
2 |
4 |
5 |
3 |
А2 |
10 |
8 |
3 |
5 |
2 |
|
|
А2 |
70 |
5 |
2 |
3 |
1 |
А3 |
25 |
1 |
9 |
4 |
3 |
|
|
А3 |
60 |
3 |
1 |
4 |
2 |
Вариант 11 Вариант 12
Завод и его возможности |
Потребности строительных площадок |
|
|
Завод и его возможности |
Потребности строительных площадок |
||||||||
В1 |
В2 |
В3 |
В4 |
|
|
В1 |
В2 |
В3 |
В4 |
||||
60 |
45 |
50 |
65 |
|
|
100 |
40 |
90 |
120 |
||||
А1 |
60 |
4 |
1 |
3 |
2 |
|
|
А1 |
180 |
12 |
8 |
6 |
5 |
А2 |
70 |
3 |
2 |
5 |
1 |
|
|
А2 |
110 |
3 |
16 |
20 |
15 |
А3 |
90 |
5 |
4 |
2 |
3 |
|
|
А3 |
60 |
15 |
10 |
7 |
8 |
Вариант 13 Вариант 14
Завод и его возможности |
Потребности строительных площадок |
|
|
Завод и его возможности |
Потребности строительных площадок |
||||||||
В1 |
В2 |
В3 |
В4 |
|
|
В1 |
В2 |
В3 |
В4 |
||||
5 |
12 |
18 |
15 |
|
|
65 |
45 |
60 |
50 |
||||
А1 |
25 |
1 |
9 |
4 |
3 |
|
|
А1 |
60 |
2 |
1 |
4 |
3 |
А2 |
15 |
4 |
1 |
6 |
4 |
|
|
А2 |
70 |
1 |
2 |
3 |
5 |
А3 |
10 |
8 |
3 |
5 |
2 |
|
|
А3 |
90 |
3 |
4 |
5 |
2 |
ЗАДАНИЕ 13. Банк может приобрести на сумму b денежных единиц акции компании А1 номинальной стоимости а1 денежных единиц, компании А2 номинальной стоимости а2 денежных единиц, компании А3 номинальной стоимости а3 денежных единиц. На конец года рынок ценных бумаг может оказаться в одном из двух состояний R1 и R2.
Специалисты
установили, что дивиденды компании Аi
для состояния рынка Rj
на конец года составят dij
% от номинальной стоимости (
).
Требуется:
придать описанной ситуации игровую схему, установить характер игры и определить игроков, указав их возможные стратегии;
составить платежную матрицу;
сформировать портфель акций банка, обеспечивающий как можно большую прибыль.
Учитывать следующие предположения:
а)
известны вероятности
и
состояния рынка
и
на конец года;
б) о вероятностях состояния рынка и на конец года ничего определенного сказать нельзя.