15. Как заряжены земная поверхность и атмосфера? Какие процессы поддерживают заряд Земли?

Хотя обычно атмосфера не считается электропроводной средой, она все же обладает небольшой проводимостью. Поэтому оставленное на воздухе заряженное тело медленно утрачивает свой заряд. Проводимость атмосферы возрастает с высотой из-за увеличения интенсивности космического излучения, уменьшения потерь ионов в условиях более низкого давления (и, следовательно, при большем среднем свободном пробеге), а также из-за меньшего количества тяжелых ядер. Проводимость атмосферы достигает максимальной величины на высоте ок. 50 км, т.н. "уровне компенсации". Известно, что между поверхностью Земли и "уровнем компенсации" постоянно существует разность потенциалов в несколько сотен киловольт, т.е. постоянное электрическое поле. Выяснилось, что разность потенциалов между некоторой точкой, находящейся в воздухе на высоте нескольких метров, и поверхностью Земли очень велика - более 100 В. Атмосфера имеет положительный заряд, а земная поверхность заряжена отрицательно. Поскольку электрическое поле - область, в каждой точке которой имеется некоторое значение потенциала, можно говорить о градиенте потенциала. В ясную погоду в пределах нижних нескольких метров напряженность электрического поля атмосферы почти постоянна. Из-за различий электропроводности воздуха в приземном слое градиент потенциала подвержен суточным колебаниям, ход которых существенно меняется от места к месту. При отсутствии локальных источников загрязнения воздуха - над океанами, высоко в горах или в полярных районах - суточный ход градиента потенциала в ясную погоду одинаков. Величина градиента зависит от всемирного, или среднего гринвичского, времени (UТ) и достигает максимума в 19 ч. Э. Эплтон предположил, что этот максимум электропроводности, вероятно, совпадает с наибольшей грозовой активностью в планетарном масштабе.

16. Напишите уравнение статики атмосферы. Каков его физический смысл?

Уравнение, описывающее изменение атмосферного давления с высотой в предположении статического равновесия, т. е. при равновесии силы тяжести и вертикальной составляющей барического градиента:

или

От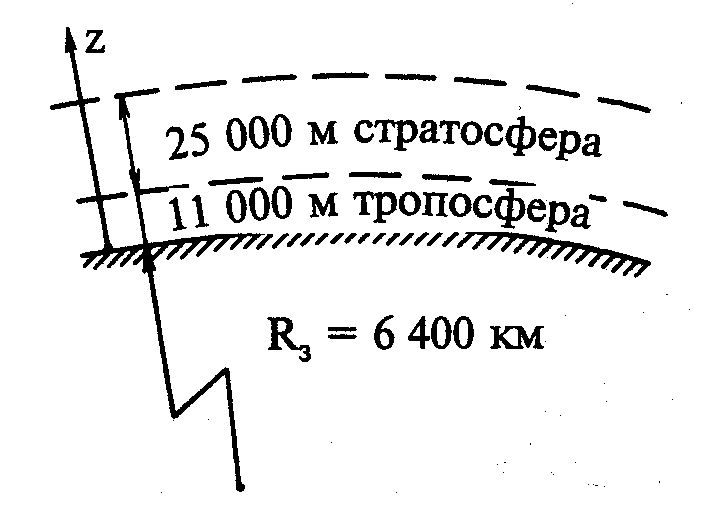 сюда следует, что распределение давления по вертикали в атмосфере определено полностью, если известен вертикальный профиль температуры и давление на каком-либо одном уровне. Физически правильно было бы использовать значениние давления на самых верхних уровнях, но в силу малой точности наблюдений, применяют давление на уровне подстилающей поверхности.

Интеграл этого уравнения называется барометрической формулой.

17. Что такое вертикальный барический градиент?

18. Напишите барометрическую формулу. Какие задачи решаются с помощью барометрической формулы?

 Барометрическая формула определяет зависимость давления или плотности газа от высоты в поле тяжести. Для идеального газа, имеющего постоянную температуру Т и находящегося в однородном поле тяжести (во всех точках его объёма ускорение свободного падения g одинаково), Б. ф. имеет следующий вид: р = p0exp [-gm.(h - h0)/RT] (1), где р — давление газа в слое, расположенном на высоте h, p0 — давление на нулевом уровне (h = h0), m — молекулярная масса газа, R — газовая постоянная, Т — абсолютная температура. Графически зависимость (1) представлена на рис. Из Б. ф. (1) следует, что концентрация молекул n (или плотность газа) убывает с высотой по тому же закону: n =n0exp [-mg (h-h0)/kT], где m — масса молекулы, k — Больцмана постоянная. Б. ф. лежит в основе барометрического нивелирования — метода определения разности высот Dh между двумя точками по измеряемому в этих точках давлению (p1 и p2). Поскольку атмосферное давление зависит от погоды, интервал времени между измерениями должен быть возможно меньшим, а пункты измерения располагаться не слишком далеко друг от друга. Б. ф. записывается в этом случае в виде: Dh = 18400· (1+at) lg (p1/p2) (в м), где t — средняя температура слоя воздуха между точками измерения, a — температурный коэффициент объёмного расширения воздуха. Погрешность при расчётах по этой формуле не превышает 0,1—0,5% от измеряемой высоты. Более точна формула Лапласа, учитывающая влияние влажности воздуха и изменение ускорения свободного падения.