Алгоритмы. Часть 2.
Пример решения
ПЕРЕМНОЖЕНИЯ 8-ми-значных чисел алгоритмом
Анатолия Карацубы.
Создать нормальный
алгоритм Маркова,
Распознающий
Язык Дика Правильных СКОБОЧНЫХ
выражений. Скобочные выражения
получаются из первых 3х уникальных
чисел в последовательности
 (если есть повтор, добавить
(если есть повтор, добавить
 ,
при 2-кратном повторе применить ТИПОВОЕ
правило создание уникальной комбинации)
переводом
,
при 2-кратном повторе применить ТИПОВОЕ
правило создание уникальной комбинации)
переводом
 .
.
Провести операции
над числами. Числа берутся в 1-ричной
записи: 3=111, 7=1111111
Вычесть
Сравнить
Умножить на 3
Умножить
(Универсальным алгоритмом)
Сложить (только
методом перегонки * на край)
Часть универсального
умножения стоит как все остальные(несколько
зависит от сложности расчёта). В каждом
случае нужно провести
(за 4 задачи)(Теорема
Кука и одноименная презентация).
Рассмотреть машину Тьюринга С языком
a,b,c,d
mod8(трехсимвольные
цепочки). Свести к КНФ. Требуемая
 ,
где
,
где
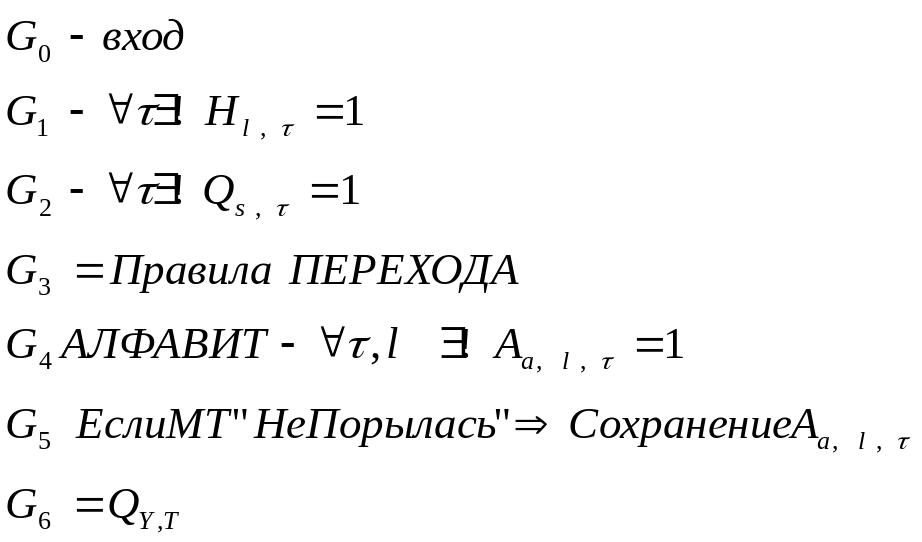 Указания:
Переменные
Указания:
Переменные
 ,
s-
состояния,
,
s-
состояния,
 - координата,
- координата,
 - время (
всегда последний индекс), конкретно,
- время (
всегда последний индекс), конкретно,
 ,
,
 где
где
 переменные координаты,
переменные координаты,
 переменные
состояния зависят от ВАШЕЙ машины
Тьюринга – пример для двух промежуточных
состояний, переменные алфавита,
переменные
состояния зависят от ВАШЕЙ машины
Тьюринга – пример для двух промежуточных
состояний, переменные алфавита,
 .
.

Наиболее сложная
под-коньюнкция
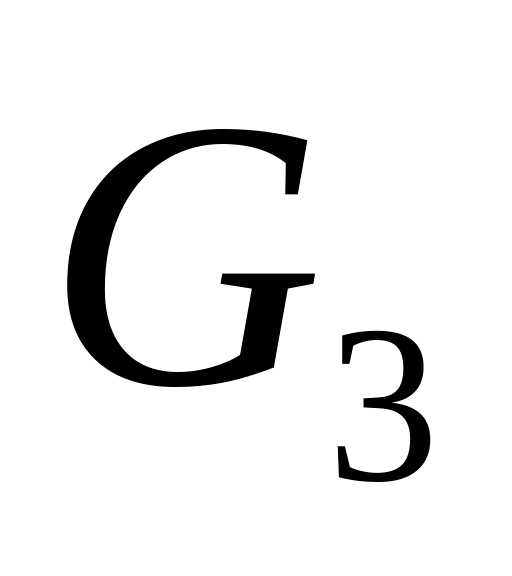 отражает специфику машины Тьюринга
отражает специфику машины Тьюринга
 ,
в том числе в тупиковых ситуациях
,
в том числе в тупиковых ситуациях
 (тупиковая
ситуация означает невыполнение
Коньюнкции). Остальные формулы базируются
на конструкции типа
(тупиковая
ситуация означает невыполнение
Коньюнкции). Остальные формулы базируются
на конструкции типа
 :
:
 или
или
 - одно единственное значение истины для
всех
.
- одно единственное значение истины для
всех
.


 - аналогично,
- аналогично,
 ,
,
 - контролирует неизменность символа в
отсутствии Каретки,
- контролирует неизменность символа в
отсутствии Каретки,
 - переход в принимающее состояние.
- переход в принимающее состояние.
т



1
Со студентом пришлось бы встречаться,
чтобы в условиях нехватки вариантов
последовательно раздать номера
персонально записывая номера, (при
большом количестве больших потоков
это очень обременительно), и это помимо
печати документа более 1000 страниц.
28


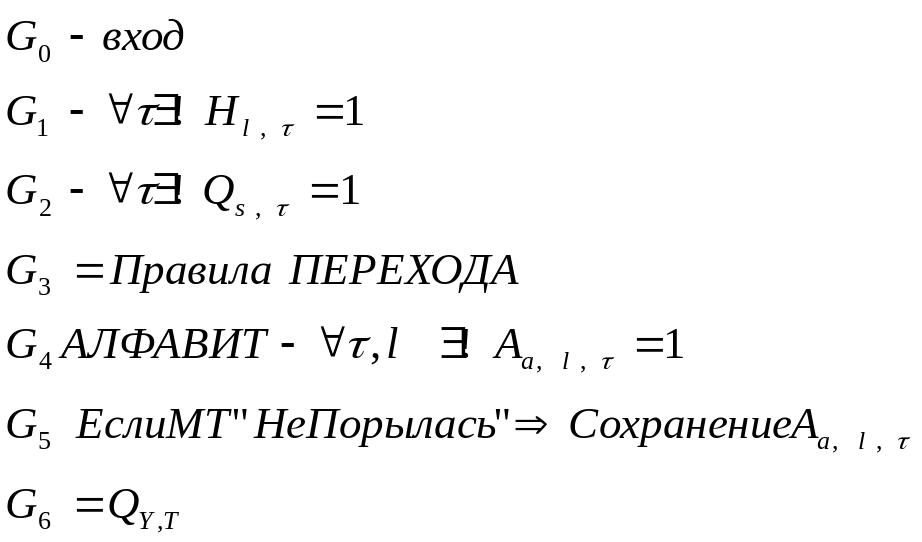 Указания:
Переменные
Указания:
Переменные
 ,
,
 где
где

 ,
в том числе в тупиковых ситуациях
,
в том числе в тупиковых ситуациях

 ,
,


