Моделирование Часть1.

67. Задача повышенной сложности.

Найти оптимум в модели использования вмещающего ландшафта. Сформировать двойственную задачу.

Рассчитать цены (труда продовольствия), реальную зарплату - долю зарплаты в ВВП, указать долю доходов от Земли в ВВП.

, где площади под поля и пастбища, соответствующая биопродуктивность и трудозатраты, - население. Территория Т, для определенности равна 50 единицам площади.

Рассмотреть ситуацию

(в предположении, что ) , (разрешается округлить до целого в большую сторону), а , .

Таким образом, получится ситуация когда . Она характерна для России. В этой ситуации цена рабочей силы отлична от 0. Доп. вопрос - рассчитать эту цену в единицах (насколько сократится население, если отвлечь 1 человека на непроизводительные работы).

Указание: чтобы задача имела решение графическим методом, ограничение рассматривать как точное равенство: вся доступная территория введена в хозяйственный оборот - . Графический метод следует применять в вертикальной полосе на плоскости этого равенства. Построить график в масштабе(т.е. с соблюдением пропорций), считая, или (на выбор) .

1. Исследовать уравнение а) 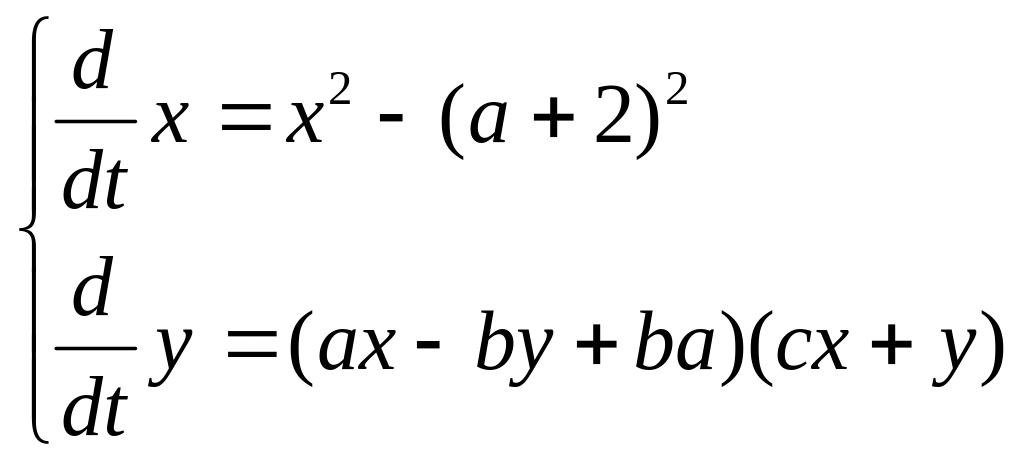б)

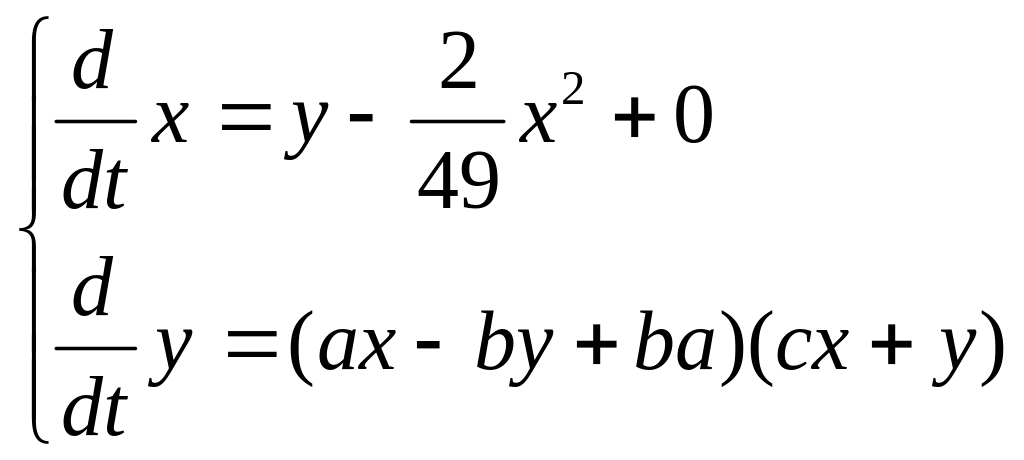
   1. Найти и построить главные изоклины

   2. Отметить равновесия

   3. Найти собственные вектора и собственные значения, классифицировать и изобразить фазовые портреты в окрестности равновесия, отметить устойчивые и неустойчивые.

   4. Вертикальные и горизонтальные изоклины отметить соответствующей вертикальной и горизонтальной штриховкой

Указание.

1. Изобразить разным цветом и стилем главные изоклины

   1. Приравнять все правые части 0

   2. Построить изоклины

2. Решить систему уравнений приравняв правые части к нулю – найти точки равновесия (а геометрически – это точки пересечения изоклин).

3. Найти коэффициенты линеаризованной системы – для этого (в аналитической форма) вычислить матрицу частных производных от вектор-функции правых частей О.Д.У.

Примечание: получившаяся матрица – это матрица функций.

4. Т.к. в точках равновесия за отсутствием постоянного слагаемого система приблизительно определяется линейной частью, вычислить записать линеаризованную систему исследовать её на тип равновесия и устойчивость в каждой из найденных точек равновесия.

5. С этой целью решив в каждой точке характеристические уравнения для матрицы системы найти собственные вектора и с. Значения. Собственные значения помогут классифицировать фазовый потрет. (а собственные вектора, в случае их нахождения, помогут уточнить основные направляющие на нём).

1. Исследовать на устойчивость

   1. ДО

   2. ОДУ

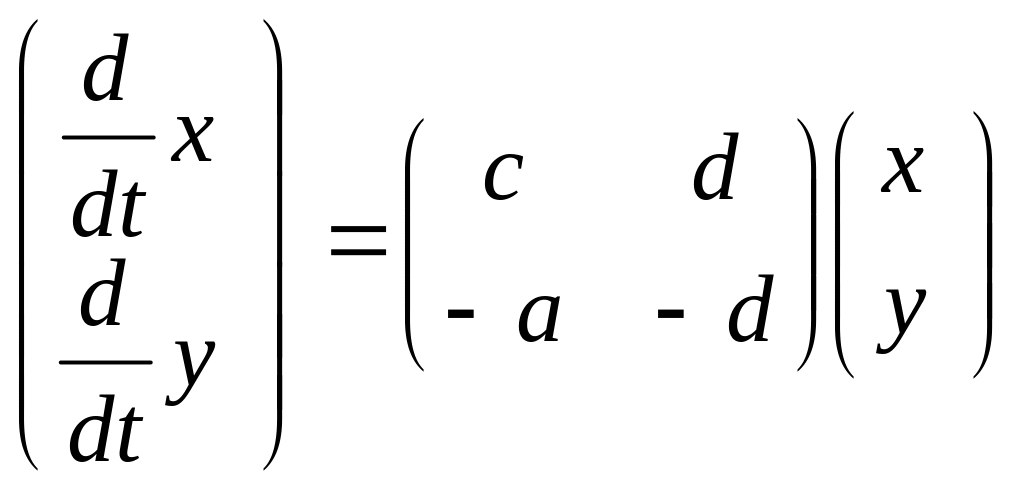
2. Исследовать на устойчивость при разных значениях параметра .

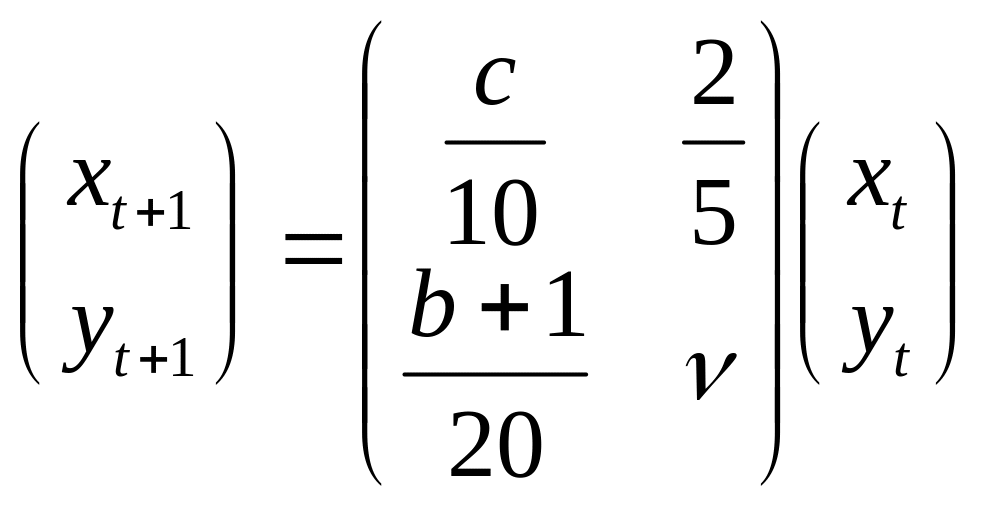3. Решить уравнение 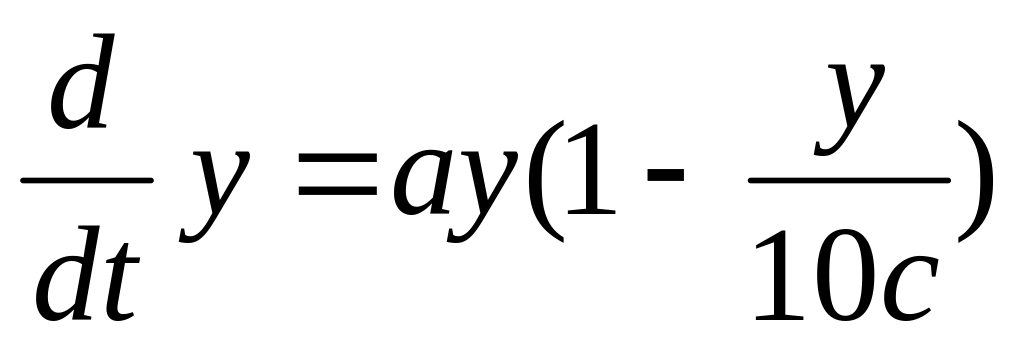, положив 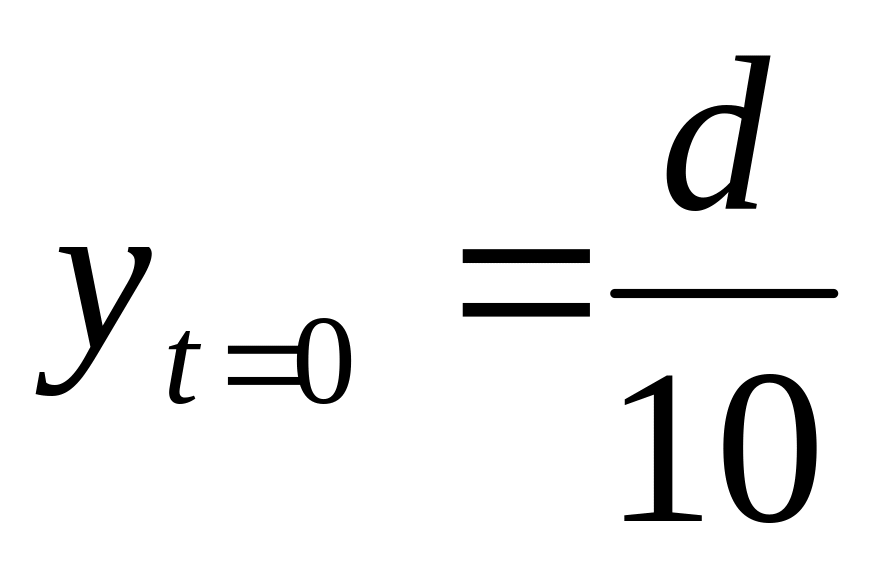указать решение для данных начальных условий. Указание разделение переменных + разложение дробей должны дать дробнолинейные функции. при интегрировании это даст (в будущем экспоненты) логарифмы

4. Для системы Чернавского найти все равновесия исследовать на устойчивость и определить тип ) 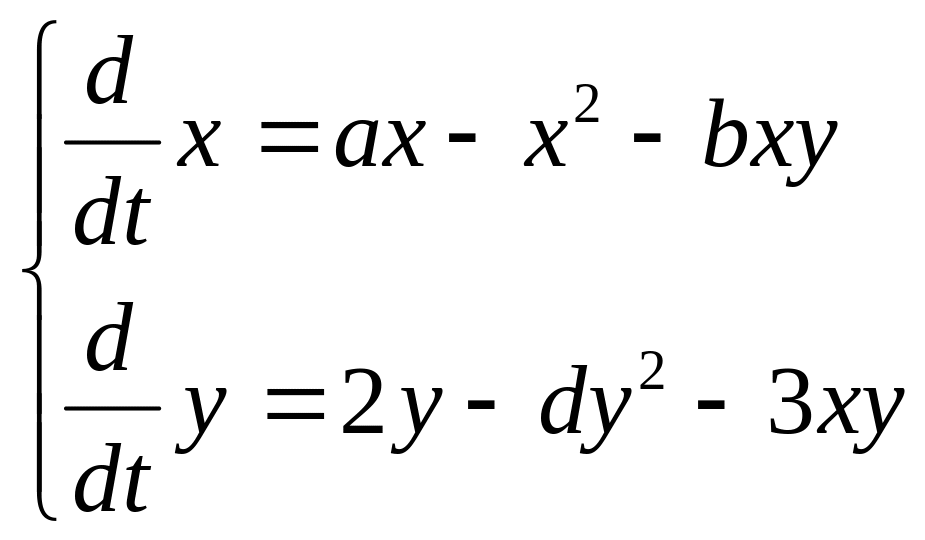. Построить портрет (использовать изоклины – см. 1е задание).

5. В модели обучения Капустина . 1)Численно найти границу областей притяжения 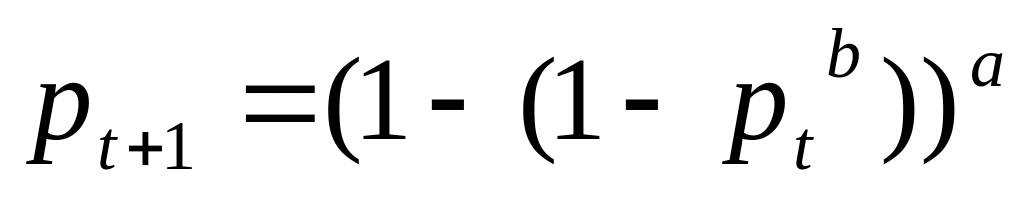и 2) бифуркацию слияния нижнего среднего равновесия в более общей модели