Теория и методы принятия решений

20. (2 у.з.) Методом ЗАПРОС (книга Ларичева) сравнить(попарно)5альтернатив a1=A2Б1B3, a2= A1Б2В1, a3= A2Б2В2, a4=A3Б1В2, a5=А1Б3В2 (без вариантов). Предпочтения задаются графами частичного порядка Паре AБ ( ) – остаток от деления на 6,АВ ( ), БВ ( ) (см.число в скобках на рисунке), 216 вариантов. По результатам попарного сравнения альтернатив на плоскости построить граф их сравнения (10 пар). в случае если при построении ЕПШ выяснится противоречие –цикл -, надлежит его исправить с момента его обнаружения произвольным образом пересмотрев предпочтения в цепочках.

21. АИ3 (За 3 задачи). Методичка Дмитриев. Презентация Анализ иерархий. Решить методом анализа иерархий

n	1	2	3	4	5	6	7	8	9	10	11
Mnxn	0	0	0,58	0,90	1,12	1,24	1,32	1,41	1,45	1,49	1,51

22. (1 условная задача)Р ассчитать 10 критериев для 4 альтернатив. Обвести кружком победителей по каждому критерию

23. Методом анализа иерархий решить задачу

24. (б)отчасти используя численные результаты предыдущего решения:

а). Сравнить две (а1,а2)-альтернативы по 3м критериям. Матрица важности критериев 1го уровня ЛПР у второго уровня М1 , М2 . Матрицы сравнения альтернатив по критериям нижнего (3^го) уровня: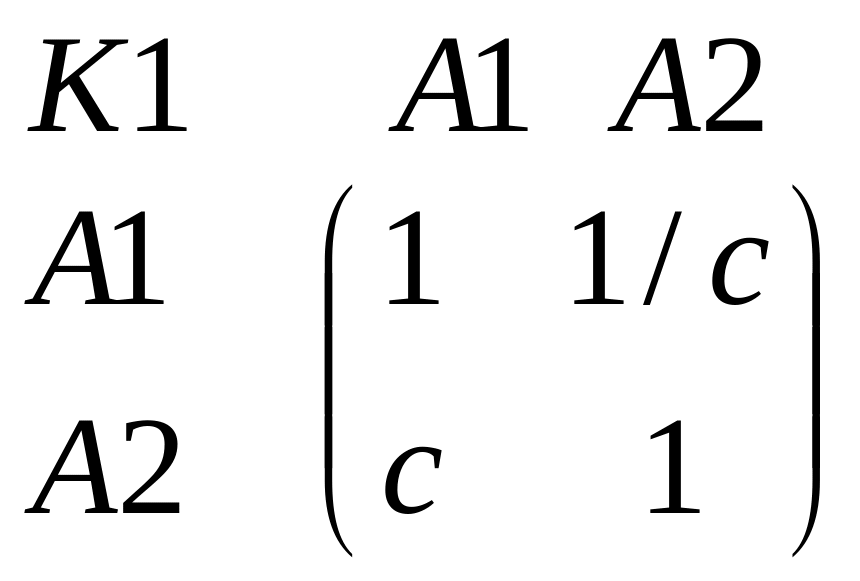 , , . Рассчитать погрешность метода с помощью индекса согласованности ( ). *Если параметр в обратносимметрической матрице оказывается нулевой заменить его на 1.

б) Рассчитать ошибку метода по формуле

**Указание: Главные собственные вектора приближенно вычислить как сумму элементов в строках . Затем отнормировать, так чтобы сумма координат составляла 1. Расчет приоритета альтернатив (в данной постановке) сведётся к сложению (нормироанных) собственных векторов последних трех матриц с коэффициентами равными координатам нормированного главного собственного вектора первой матрицы, а расчет СЗ , где А – матрица парных сравнений.

25. (2 условные задачи)Сравнить методом ELECTRE 4 альтернативы по критериям

При весах критериев .

Чтобы устранить неопределённость сумму коэффициентов согласия α и несогласия β можно держать 1: β=1-α.

26. Пример двухуровневый анализ иерархий (классический ВАРИАНТ)

Исследование Операций

27. Простейшая задача (1 условная задача)http://video.yandex.ru/users/o-krivosheev/view/302/# Жадный алгоритм (Крускалла) Построить минимальное остовное дерево.

Указание ПРЕПОДАВАТЕЛЯМ – с этой задачи рекомендуется начинать СЕМЕСТР.

Указание: Ответ должен содержать все шаги алгоритма (включаемые в сеть дорог отрезки) в правильной последовательности их выбора. В алгоритме построения минимального остовного дерева последовательно выбираются ребра (отрезки возможных путей) минимальные из оставшихся. (Презентация ИССЛЕДОВАНЕ ОПЕРАЦИЙ)

28. Комм5х5 (Засчитывается за 4 условные задачи) 2 пары) (Презентация КОММИВОЯЖЁР) Самая сложная задача исследования операций . Методом ветвей и границ требуется найти Кратчайший маршрут объезда 5 городов с возвратом в исходный, при КОТОРОМ КАЖДЫЙ ГОРОД ПОСЕЩАЕТСЯ в ТОЧНОСТИ 1 раз(в матрице даны цены проезда из «левого» города в «верхний»).

29. Ком4х4, (3 задачи – засчитывается только 1 из двух задач) Сокращённая задача Коммивояжера 4х4 Презентация КОММИВОЯЖЁР

Проверяется по дереву ветвления, в вершинах дерева отобразить нижние оценки целевых функций, на рёбрах дерева д.б. обязательно отображены все θ(правый поворот), все ΔZ(сумма констант редуцирования). В ответе дается цепочка Рёбер вида (1,k)(k,l)(l,m)..(r,1)(по размеру задачи), стоимость маршрута состоит из начальной нижней оценки и её приращений ΔZ(если были только ВЫЧЁРКИВАНИЯ – левые ПОВОРОТЫ) и – что бывает очень редко - ΔZ и θ, если КРОМЕ левых ПОВОРОТОВ присутствовали один или несколько правых поворотов. Провести проверку стоимости ПОЛУЧЕНОГО решения по исходной матрице, объяснить причины несовпадения – если имелись (не совпадений быть не должно).

30. 1. (irr)(1 задача) (45 мин) Рассчитать рентабельность проекта на рисунке. Время между платежами 1,5 года.

Сравнить IRR cо ставкой банка, взятой на память (или же из Яндекса), принять решение, целесообразны ли инвестиции в данный проект. Ответ (равно решение) данные без размерности не засчитываются.

31. (2 задачи, пара 90 мин). Алгоритмом Форда-Фалкерсона найти максимальный поток в сети

(Презентация ИССЛЕДОВАНЕ ОПЕРАЦИЙ) При решении условие (только САМ граф перерисовывается 5-6 раз). В ответе дать СУММУ потоков, матрицу потоков (по матрице проверить, что сума потоков равна сумме вытекающих из S и приходящих в F) и построить граф потоков (до заполнения матрицы).

32. (2 задачи, почти пара)Решить задачу поиска кратчайших путей. (Презентация ИССЛЕДОВАНЕ ОПЕРАЦИЙ)

Образец оформления

Алгоритм.

Начало.

В стартовой вершине S ставим (0,-) –ВЕЧНАЯ МЕТКА (Она читается 0 «из ниоткуда»).

Из стартовой вершины мы рассылаем ВО все соседние ВЕРШИНЫ ВРЕМЕННЫЕ МЕТКИ «метастазы» - в них ставится сумма 0 (из позиции (0,-)) и расстояния до стартовой вершины S

33. (СПУ1) Рассчитать минимальное время выполнения проекта.

34. (СПУ2): чтобы не производить сложных расчетов – заменим в предыдущем условии ВСЕ веса на их разности с 10, взятые по модулю(таким образом все веса положительны). Перейдём в представление УЗЕЛ-РАБОТА. (построить граф на весь лист, предварительно повернув его альбомно) Пользуясь 10ти компонентным представлением отразить сведения о работе (название, центр-длительность, времена начала-окончания в углах. Запасы в серединах сторон. По одной из этих задач построить график Ганта. Задача обязательна по дисциплине управление проектами.

35. (1 условная задача)Рассчитать методом динамического программирования (решения полученные другими способами не принимаются) кратчайший путь по системе дорог.

Ответ:

37. Решить задачу линейного программирования (прямая задача 2 условные задачи, двойственная 1 условная задача, все вместе -3 у.з.)

Условие:

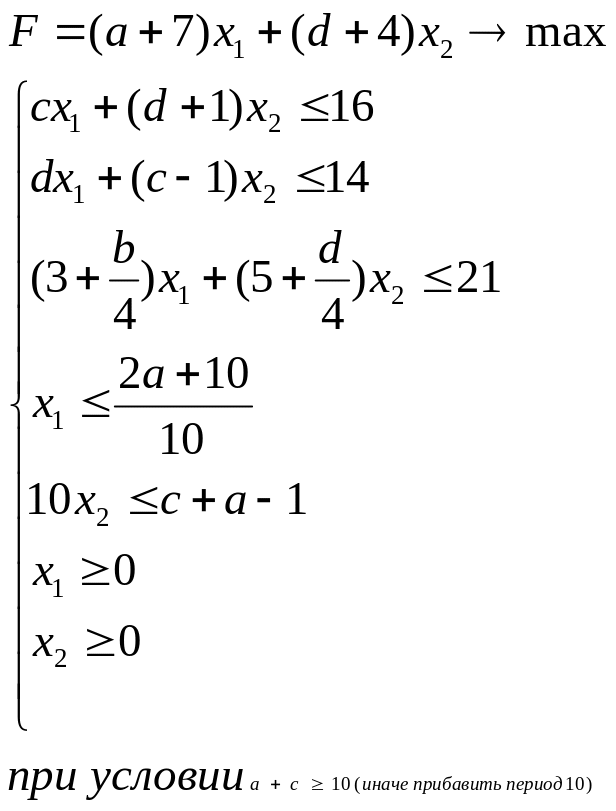
38. Решить задачу двойственную к предыдущей. Сравнить ответ. (задачи решаются комплектом).

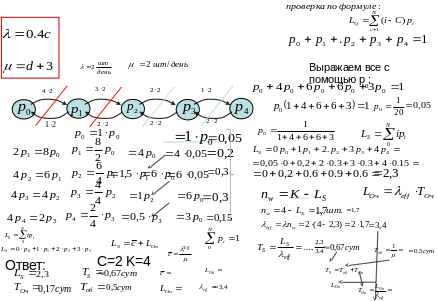
39. (2 условных задачи)Решить задачу теории массового обслуживания

2. Дано , интенсивность поломок оборудования (где (условие оптимизировано под данные из Ф.И.О.), если не так ПРИБАВИТЬ ровно 10: ) –

3. - скорость(интенсивность) ремонта. Ремонтом занимаются два человека, обслуживающих К=4 автомата (См. Хемеди А Таха Исследование операций).

4. 

40. (устаревшая задача) Решить графическим методом. В решении должны фигурировать для каждого ограничения пары точек(1 точка это две координаты, их порядок важен) удовлетворяющие соответствующему равенству, тестовая точка - (0,0) или другая, и то, отвечает она неравенству или нет. На графике: градиент, отложенный от начала координат, прямые, соответствующие ограничениям, штриховка по одну из сторон каждой прямой, включая координатные оси, обозначающая полупространство определяемое соответствующим неравенством и их пересечение - область допустимых решений должна быть обведена специальным цветом. В ответе должны быть даны координаты точки пересечения активных ограничений

(задача оптимизации производства: - объёмы выпуска на конвейерах, коэффициенты при них в неравенствах – объёмы ресурсных затрат, числа в правой части – наличествующий ресурс каждого типа, - прибыль, коэффициенты при переменных (компоненты вектора градиента) – цены продукции ).