- •Вопрос 1.
- •Вопрос 2: Виды движений мт и атт: -поступательное; -вращательное вокруг неподвижной оси; - плоское; -движение вокруг неподвижной точки; -свободное движение.
- •Вопрос 3: движ под углом к горизонту
- •Вопрос 4: Траектория движения. Криволинейное движение. Нормальное и тангенциальное ускорения при криволинейном движении.
- •Вопрос 5: Вращательное движение. Угловая скорость и угловое ускорение. Кинематические уравнения для вращательного движения.
- •Вопрос 6: Связь между линейными и угловыми характеристиками мт и атт при их вращении вокруг точки или оси
- •Вопрос 7 Понятия динамики. Три закона Ньютона. Сила, импульс. Основное уравнение динамики поступательного движения. Силы в механике.
- •4)Гравитац. Сила
- •Вопрос 8: Инерциальные системы отсчета. Собственная и лабораторные исо. Механический принцип относительности Галилея. Преобразования Галилея.
- •Вопрос 9:Система материальных точек. Закон сохранения импульса. Абсолютно упругий и неупругие удары.
- •13. Силы упругости. Упругие деформации. Закон Гука. Потенциальная энергия в поле упругих сил
- •14. Силы трения. Уравнение динамики поступательного движения при наличии трения- на примере
- •15. Гравитационное взаимодействие. Сила всемирного тяготения. Сила тяжести и невесомостью. Фундаментальный физический закон Галилея
- •16.Работа гравитационных сил. Потенциал и напряженность гравитационного поля. Космические скорости.
- •17.Основные динамические характеристики движения
- •18.Вращательное движение. Момент импульса Lr и момент силы м мт относительно точки. Главный момент системы сил.
- •20. Уравнение моментов. Законы изменения и сохранения момента импульса при вращении мт вокруг точки и атт, закрепленного в одной точке
- •21. Пара сил. Центр тяжести (цт) механической системы
- •23. Закон изменения и сохранения момента импульса мт и атт. Скамья Жуковского.
- •24. Момент инерции мт и атт. Теорема Штейнера. Расчет момента инерции тонкого стержня.
- •Теорема Штейнера:
- •Вопрос 26 : Свободные гармонические механические колебания и их характеристики. Математический и физический маятники.
- •Вопрос 27: Векторная диаграмма и сложение одинаково направленных гармонических колебаний
- •28) Сложение взаимно перпендикулярных гармонических колебаний.
- •29) Дифференциальное уравнение свободных гармонических механических колебаний и его решение. Энергия колебаний. Физический маятник.
- •30) Затухающие гармонические колебания. Коэффициент затухания и логарифмический декремент затухания. Время релаксации.
- •31.Вынужденные колебания. Расчёт амплитуды и фазы
- •32. Резонанс механических колебаний
- •33. Уравнения упругих волн, плоской и сферической. Принцип суперпозиции волн. Фазовая и групповая скорости
- •34. Волновое уравнение и его решение. Физический смысл волнового уравнения. Скорость распространения волн в различных средах.
- •35. Звук. Распространение упругих волн в упругой среде. Характеристики упругих волн.
- •36. Волновой перенос энергии и его характеристики: поток, плотность потока, интенсивность. Вектор Пойтинга.
- •37. Границы применимости классической механики. Теория относительности. Постулаты Эйнштейна. Преобразования Лоренца.
- •39. Теорема сложения скоростей в сто.
- •40. Импульс в релятивистской механике.
- •41. Релятивистские законы Ньютона. Связь между энергией и импульсом частицы
- •43. Корпускулярно-волновой дуализм. Длина волны де Бройля. Квантование электронных орбит атома в модели де Бройля. Соотношения неопределенностей.
- •44. Предмет квантовой механики. Волновая функция, ее свойства и статистический смысл.
- •45. Временное и стационарное уравнение Шредингера. Решения.
- •46. Решение уравнения Шредингера для свободной частицы.
- •Вопрос 47: Уровни энергии и волновая функция частицы, находящейся в прямоугольной потенциальной яме.
- •48. Квантовый гармонический осциллятор.
- •50. Молекулярная физика, макросистемы и положения мкт. Идеальный газ. Эргодическая гипотеза. Постоянные в молекулярной физике. Основное уравнение молекулярно-кинетической теории – вывод.
- •51.Степени свободы молекул. Закон Больцмана о равномерном распределении энергии по степеням свободы. Внутренняя энергия идеального газа.
- •52. Эффективный диаметр, средние длина и время свободного пробега, число столкновений в единицу времени для молекул идеального газа.
- •53. Законы идеального газа, адиабатический процесс – вывод уравнения Пуассона.
- •54. Политропический процесс – вывод уравнения состояния.
- •55. Термодинамика. Термодинамические система и параметры, термодинамическое равновесие. Равновесный процесс. Внутренняя энергия – функция состояния.
- •56. Пути изменения внутренней энергии. Теплота и работа. Первое начало термодинамики. Работа расширяющегося газа.
- •58.Теплоёмкость идеального газа
- •Вопрос 59: Работа – функция процесса. Работа, совершаемая газом при изотермическом и изохорном процессах. Изохорический процесс
- •Вопрос 60:Работа – функция процесса. Работа, совершаемая газом при изобарическом процессе.
- •63. Второе начало термодинамики. Самопроизвольные и несамопроизвольные процессы. Равенство и неравенство Клаузиуса.
- •66. Третье начало термодинамики (теорема Нернста).
- •71.Эффект Джоуля- Томсона отрицательный
- •72. Эффект Джоуля-Томсона – положительный и интегральный.
- •75. Явления переноса: внутреннее трение.
- •76 Явления переноса: диффузия и теплопроводность
45. Временное и стационарное уравнение Шредингера. Решения.
Общее уравнение Шредингера называют также уравнением Шредингера, зависящим от времени. Оно является основным уравнением нерелятивистской квантовой механики. уравнение должно быть уравнением относительно волновой функцией Ψ(х, у, z, t). Также это уравнение должно обладать некоторыми чертами, присущими волновому уравнению для упругих волн, поскольку оно призвано учитывать волновые свойства микрочастиц.
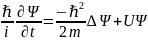
Стационарное
уравнение Шредингера.

Функции
 ,
являющиеся решениями уравнения,
называются собственными функциями.
Уравнения в ряде случаев имеют решения
не при всех значениях энергии Е, а лишь
при определенных ее значениях. Значения
энергии Е, при которых имеет место
решение уравнения Шредингера, называют
собственными значениями энергии.
Собственные значения энергии Е могут
образовывать как не-прерывный, так и
дискретный ряд значений энергии. В
первом случае говорят о непрерывном,
во втором − о дискретном спектре энергии.
,
являющиеся решениями уравнения,
называются собственными функциями.
Уравнения в ряде случаев имеют решения
не при всех значениях энергии Е, а лишь
при определенных ее значениях. Значения
энергии Е, при которых имеет место
решение уравнения Шредингера, называют
собственными значениями энергии.
Собственные значения энергии Е могут
образовывать как не-прерывный, так и
дискретный ряд значений энергии. В
первом случае говорят о непрерывном,
во втором − о дискретном спектре энергии.
46. Решение уравнения Шредингера для свободной частицы.
Рассмотрим волновую функцию свободной микрочастицы, которая имеет определенные значения импульса р и энергии Е, т. е. движется со скоростью υ, например, вдоль оси Ох (ру = рz = 0). Так как из опытов следует, что параллельный пучок элементарных частиц обладает свойствами плоской волны распространяющейся в направлении скорости частиц, то рассмотрим в общем виде плоскую волну распространяющуюся вдоль Ох. Запишем волновую функцию свободной частицы в комплексном виде по аналогии с уравнением плоской волны.
Ψ=
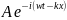 =Acos(wt-kx)
– isin(wt-kx) (8.6.1)
=Acos(wt-kx)
– isin(wt-kx) (8.6.1)
Преобразуем выражение (8.6.1), используя формулы взаимосвязи импульса р и энергии Е частицы (корпускулярных характеристик) с волновым числом k и циклической частотой ω (с волновыми характеристиками частицы)
E=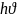 =
=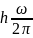 ⇒
ω=
⇒
ω=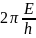 =
=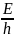 (8.6.2)
(8.6.2)
 (8.6.3)
(8.6.3)
Подставим (8.6.2−8.6.3) в уравнение (8.6.1) и получим
 (8.6.5)
(8.6.5)
Применим к ψ оператор Лапласа и получим уравнение Шредингера для свободной частицы
Δψ+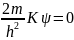
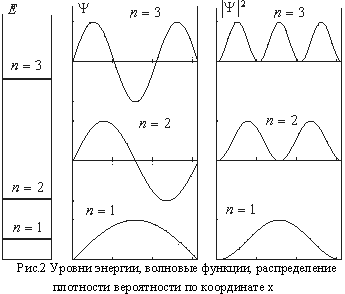
Вопрос 47: Уровни энергии и волновая функция частицы, находящейся в прямоугольной потенциальной яме.
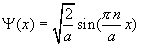
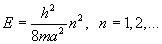
Волновая функция и энергия.
48. Квантовый гармонический осциллятор.
Квант. Гарм.
Осциллятор - определяется как повед.
частиц m
с пот. энергией U(x)=
Потенциальная энергия такого осциллятора имеет вид
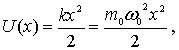
|
(4.77) |
где 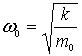 -
собственная частота классического
гармонического осциллятора. Таким
образом, квантово-механическая задача
о гармоническом осцилляторе сводится
к задаче о движении частицы в параболической
потенциальной яме.
-
собственная частота классического
гармонического осциллятора. Таким
образом, квантово-механическая задача
о гармоническом осцилляторе сводится
к задаче о движении частицы в параболической
потенциальной яме.
В квантовой механике для решения задачи о гармоническом осцилляторе нужно решить уравнение Шредингера с потенциальной энергией
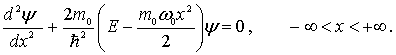
|
(4.78) |
Выражая, согласно,
энергию осциллятора ![]() через
через ![]() ,
получаем
,
получаем
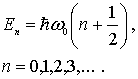
49. Прохождение частицы через барьер. Туннельный эффект.
Туннельный эффект (туннелирование) – преодоление частицей потенциального барьера, когда её энергия Е меньше высоты барьера U0.
При Е > U0 есть вероятность того, что частица отразится от барьера и будет двигаться в другую сторону.
При Е < U0 частица окажется в области x > l, где l – ширина барьера.
Вероятность проникновения электрона через потенциальный барьер зависит от высоты барьера U0, его ширины l, где m – масса частицы, E – ее энергия, h – постоянная Планка (ћ = h/2π).
Коэффициент прозрачности потенциального барьера: