3.2. Перевод из одной системы счисления в другую и простейшие арифметические операции. Перевод целых чисел

Пусть Aц- целое десятичное число. Тогда в его разложении отсутствуют коэффициенты с отрицательными индексами, и его можно представить в виде:

Aц=an-1*2n-1+an-2*2n-2+...+a0*20

Разделим число Aц на 2. Частное будет равно

an-1*2n-2+...+a1

а остаток равен a0

Полученное неполное частное опять разделим на 2, остаток от деления будет равен a1

Если продолжить процесс деления, то на n-м шаге получим набор цифр

a0, a1, a2..., an-1

которые входят в двоичное представление числа Aц и совпадают с остатками при последовательном делении данного числа на 2. Но мы их получили в порядке, обратном порядку расположения числа Aц:

Aц=an-1an-2...a1a0

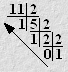
Пример: Перевести десятичное число 11 в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) удобнее изобразить так.

Записывая остатки от деления в направлении, указанном стрелкой, получим:1110=10112.

3.4.Перевод дробных чисел

1) Основание новой системы счисления выразить в десятичной системе и все последующие действия производить в десятичной системе счисления;

2) последовательно умножать данное число и получаемые дробные части произведений на основе новой системы до тех пор, пока дробная часть произведения не станет равной нулю или не будет достигнута требуемая точность представления числа в новой системе счисления;

3) полученные целые части произведений, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;

4) составить дробную часть числа в новой системе счисления, начиная с целой части первого произведения.

Пример: Перевести десятичную дробь 0,1875 в двоичную, восьмеричную и шестнадцатеричную системы.

Здесь вертикальная черта отделяет целые части чисел от дробных частей.

Отсюда: 0.187510=0.00112=0.148=0.316

Перевод из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно.

При переводе в восьмеричную систему счисления двоичное число разбиваем на группы по 3 цифры справа налево начиная с младшего разряда.

Затем каждую тройку цифр заменяем соответственно цифрой восьмеричной системы счисления.

Дробную часть разбиваем от запятой вправо на группы по 3 цифры.

Обратный переход - от восьмеричной системы счисления к двоичной - осуществляется заменой каждой восьмеричной цифры ее двоичным эквивалентом (тремя двоичными цифрами).

Для шестнадцатеричной системы счисления - четырьмя двоичными цифрами.

Таблицы переводов. Двоичная – восьмеричная