Как найти объем тела вращения, если фигура ограничена параметрически заданной линией?
Актуализируем формулу, выведенную в
начале урока: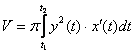 
.
Общая методика решения точно такая же,
как и при нахождении площади. Выдерну
немногочисленные задачи из своей
копилки:
Пример 8
Найти объем тела, образованного вращением
вокруг оси
криволинейной
трапеции, ограниченной линией 
,
если 
.
Решение: всё подано в лучшем
виде, осталось не оплошать в вычислениях:
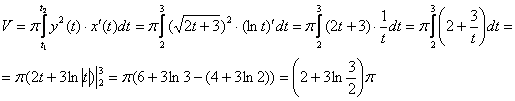
Ответ: 
Теперь ваш черёд:
Пример 9
Найти объем тела, образованного вращением вокруг оси эллипса
Данная поверхность вращения
называется эллипсоидом
вращения или сфероидом.
А
в случае равенства 
получится
в точности сфера и,
соответственно, объём ограниченного
ей шара. Кстати, объём данного тела
вращения довольно легко вычислить и в
декартовых координатах, поскольку
подынтегральная функция в
формуле
ликвидирует
квадратный корень. Желающие могут
выразить «игрек» из уравнения
и
решить задание вторым способом.
Помимо простейших примеров вполне могут
встретиться задачи, где придётся
выполнить чертёж и находить объём тела
вращения как разность объемов тел
вращения (или наоборот, сумму), то есть
использовать уже знакомые из статьи Объем
тела вращения приёмы.
Кроме того, по аналогии с предыдущим
параграфом, легко вывести вторую
формулу: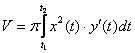 
,
с помощью которой рассчитывается объём
тела вращения вокруг оси ординат. Но
вероятность встретить такие вещи крайне
мала, по крайне мере, лично я не припоминаю,
что решал такие задания – вся надежда
на вас =)
Желаю успехов!
Решения и ответы:
Пример 3: Решение:
вычислим площадь первой арки циклоиды.
Значение параметра изменяется в
пределах
.
Найдём
производную: 
.
По
формуле:
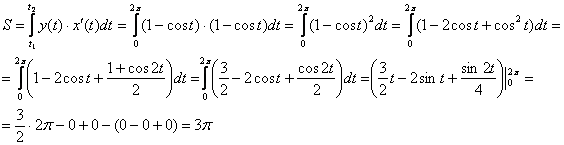Ответ: 
Пример 5: Решение:
уравнения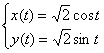 
задают
окружность с центром в начале координат,
радиуса 
.
Уравнение
определяет
прямую, параллельную оси ординат.
Поскольку 
,
то необходимо вычислить площадь
заштрихованной на чертеже фигуры:
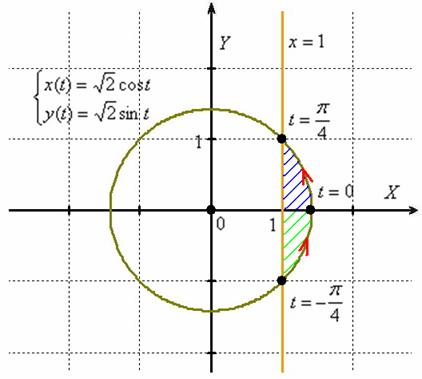Найдём
пределы изменения параметра, для этого
подставим
в
параметрическое уравнение 
:
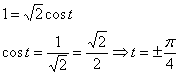Нижней
точке соответствует значение 
,
верхней точке – значение 
.
Так
как фигура симметрична относительно
оси
,
то вычислим площадь в верхней полуплоскости
(синяя штриховка), а результат
удвоим.
Функция 
убывает
на промежутке 
,
поэтому:
Ответ: 
Пример 7: Решение:
выполним чертёж:
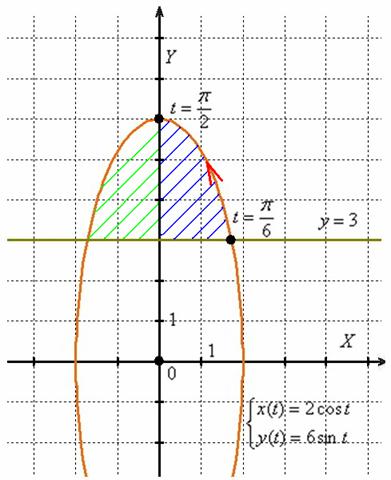Фигура
симметрична относительно оси ординат,
вычислим часть площади в правой
полуплоскости, результат удвоим. Найдём
значения параметра, при которых эллипс
пересекается с прямой 
.
Для этого подставим
в
параметрическое уравнение 
:
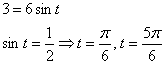(решения
быстро отыскиваются по графику
синуса либо тригонометрической
таблице).
Подставим 
в
параметрическое уравнение 
:
–
таким образом, значение 
задаёт
правую (нужную нам) точку (поскольку
получена именно её «иксовая»
координата).
Проверим, что
очевидное значение 
задаёт
верхнюю точку:
,
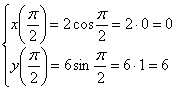что и требовалось проверить.
По
формуле:
Примечание:
в данном случае при изменении параметра
от 
до 
направление
«прорисовки» дуги совпадает с
направлением оси ординат (так как
растёт),
поэтому дополнительного вопроса с
модификацией формулы не возникло.
Ответ: 
Пример 9: Решение:
в силу симметрии эллипса, вычислим объём
тела вращения в правой полуплоскости,
результат удвоим. При изменении параметра
в пределах 
функция 
убывает,
поэтому:
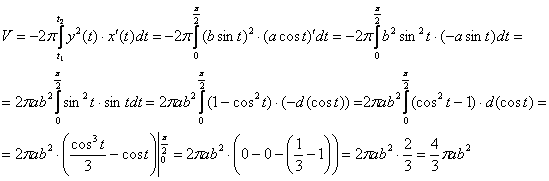Ответ: 
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)