Найти площадь эллипса

Очевидно, что параметрические функции периодичны, и  . Казалось бы, можно заряжать формулу, однако не всё так прозрачно. Выясним направление, в котором параметрические уравнения «вычерчивают» эллипс. В качестве ориентира найдём несколько точек, которые соответствуют наиболее простым значениям параметра:

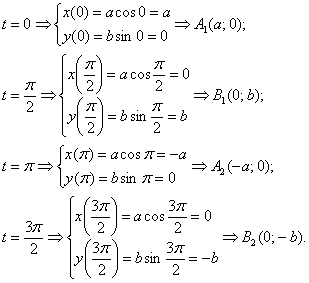
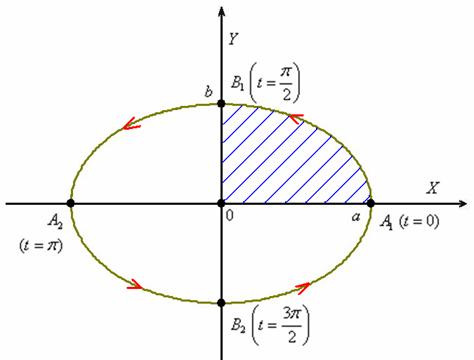
Легко уловить, что при изменении параметра «тэ» от нуля до «двух пи» параметрические уравнения «вычерчивают» эллипс против часовой стрелки: В силу симметричности фигуры, вычислим часть площади в 1-ой координатной четверти, а результат умножим на 4. Здесь мы наблюдаем принципиально такую же картину, которую я комментировал чуть выше: параметрические уравнения «прорисовывают» дугу эллипса «в противоход» оси  , но площадь фигуры считается слева направо! Поэтому  нижнемупределу интегрирования соответствует значение  , а верхнему пределу – значение  .

Как я уже советовал на уроке Площадь в полярных координатах, учетверить результат лучше сразу же:

Интеграл   (если у кого-то вдруг обнаружился такой невероятный пробел) разобран на уроке Интегралы от тригонометрических функций.

Ответ: 

По сути, мы вывели формулу для нахождения площади эллипса. И если на практике вам встретится задача с конкретными значениями «а» и «бэ», то вы легко сможете выполнить сверку/проверку, поскольку задача решена в общем виде.

Площадь эллипса рассчитывается и в прямоугольных координатах, для этого из уравнения   необходимо выразить «игрек» и решить задачу точь-в-точь по образцу Примера №4 статьи Эффективные методы решения определённых интегралов. Обязательно посмотрите на этот пример и сравните, насколько проще вычислить площадь эллипса, если он задан параметрически.

И, конечно же, чуть не забыл, параметрические уравнения   могут задавать окружность либо эллипс в неканоническом положении.

Пример 3

Вычислить площадь одной арки циклоиды 

Чтобы решить задачу, нужно знать, что такое циклоида или хотя бы чисто формально выполнить чертеж. Примерный образец оформления в конце урока. Впрочем, не буду вас отправлять за тридевять земель, на график этой линии можно посмотреть в следующей задаче:

Пример 4

Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями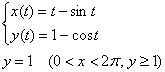 

Решение: параметрические уравнения   задают циклоиду, и ограничение   указывает на тот факт, что речь идёт о её первой арке, которая «прорисовывается», когда значение параметра изменяется в пределах  . Заметьте, что здесь «правильное» направление этой «прорисовки» (слева направо), а значит, не возникнет заморочек с пределами интегрирования. Но зато появится куча других прикольных вещей =) Уравнение   задаёт прямую, параллельную оси абсцисс и дополнительное условие   (см. линейные неравенства) сообщает нам о том, что нужно вычислить площадь следующей фигуры:

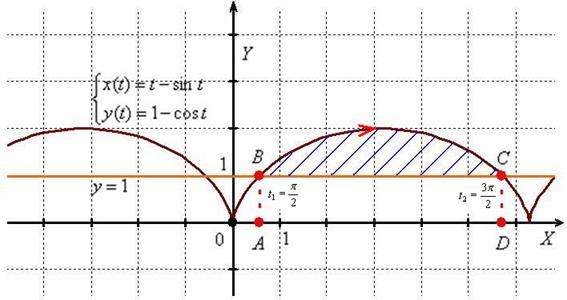
Искомую заштрихованную фигуру я буду ассоциативно называть «крышей дома», прямоугольник   – «стеной дома», а всю конструкцию (стена + крыша) – «фасадом дома». Хотя это сооружение больше напоминает какой-то коровник =)

Чтобы найти площадь «крыши» необходимо из площади «фасада» вычесть площадь «стены».

Сначала займёмся «фасадом». Для нахождения его площади нужно выяснить значения  , которые задают точки пересечения прямой   с первой аркой циклоиды (точки   и  ). В параметрическое уравнение   подставим  :

Тригонометрическое уравнение   легко решить, банально взглянув на график косинуса: на промежутке   равенству   удовлетворяют два корня:  . В принципе, всё понятно, но, тем не менее, перестрахуемся и подставим их в уравнение  :

 – это «иксовая» координата точки  ;

 – а это «иксовая» координата точки  .

Таким образом, мы убедились в том, что значение параметра   соответствует точке  , а значение   – точке  .

Вычислим площадь «фасада». Для более компактной записи функция   часто дифференцируется прямо под интегралом:

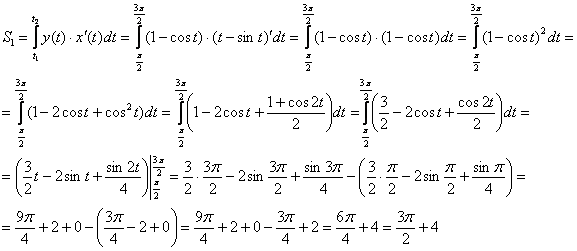
Площадь «стены» можно вычислить «школьным» методом, перемножив длины смежных сторон прямоугольника. Длина   очевидна, осталось найти  . Она рассчитывается как разность «иксовых» координат точек «цэ» и «бэ» (найдены ранее):

Площадь «стены»: 

Разумеется, её не стыдно найти и с помощь простейшего определённого интеграла от функции    на отрезке  :

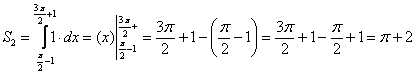
В результате, площадь «крыши»:

Ответ: 

И, конечно же, при наличии чертежа прикидываем по клеточкам, похож ли полученный результат на правду. Похож.

Следующая задача для самостоятельного решения:

Пример 5

Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями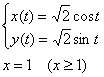 

Кратко систематизируем алгоритм решения:

– В большинстве случаев придётся выполнить чертёж и определить фигуру, площадь которой требуется найти.

– На втором шаге следует понять, каким образом рассчитывается искомая площадь: это может быть одиночная криволинейная трапеция, может быть разность площадей, может быть сумма площадей – короче говоря, все те фишки, которые мы рассматривали на урокеВычисление площади с помощью определённого интеграла.

– На третьем шаге надо проанализировать, целесообразно ли пользоваться симметрией фигуры (если она симметрична), после чего узнать пределы интегрирования (начальное и конечное значение параметра). Обычно для этого необходимо решить простейшее тригонометрическое уравнение – здесь можно использовать аналитический метод, графический метод или бесхитростный подбор нужных корней по тригонометрической таблице.

! Не забываем, что параметрические уравнения могут «прорисовывать» линию и справа налево, в этом случае делаем соответствующую оговорку и поправку в рабочей формуле.

– И на завершающем этапе проводятся технические вычисления. Правдоподобность полученного ответа всегда приятно оценить по чертежу.

А сейчас долгожданная встреча со звёздой:

Пример 6

Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями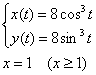 

Решение: кривая, заданная уравнениями 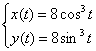  является астроидой, и линейное неравенство   однозначно определяет заштрихованную на чертеже фигуру:

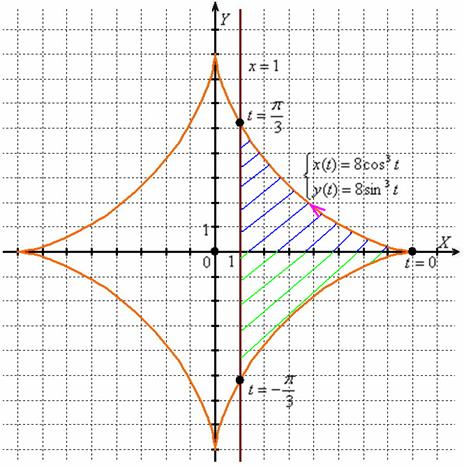
Найдём  значения параметра, которые определяют точки пересечения прямой и астроиды. Для этого подставим   в параметрическое уравнение  :

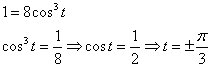Способы решения подобного уравнения уже перечислены выше, в частности, эти корни легко подбираются по тригонометрической таблице.

Фигура симметрична относительно оси абсцисс, поэтому вычислим верхнюю половинку площади (синяя штриховка), а результат удвоим.

Подставим значение   в параметрическое уравнение  :  В результате получена «игрековая» координата верхней (нужной нам) точки пересечения астроиды и прямой.

Правой вершине астроиды, очевидно, соответствует значение  . Выполним на всякий случай проверку: 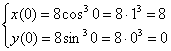, что и требовалось проверить.

Как и в случае с эллипсом, параметрические уравнения «прорисовывают» дугу астроиды справа налево. Для разнообразия оформлю концовку вторым способом: при изменении параметра в пределах   функция   убывает, следовательно (не забываем удвоить!!):

Интеграл получился довольно громоздкий, и чтобы «не таскать всё за собой» тут лучше прервать решение и преобразовать подынтегральную функцию отдельно. Стандартнопонижаем степень с помощью тригонометрических формул:

Годится, в последнем слагаемом подведём функцию под знак дифференциала:

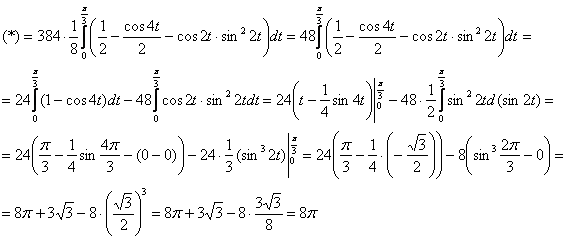
Ответ: 

Да, тяжеловато приходится со звёздами =)

Следующее задание для продвинутых студентов:

Пример 7

Вычислить площадь фигуры, ограниченной линиями, заданными уравнениями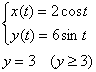 

Для его решения будет достаточно материалов, которые мы уже рассмотрели, но привычный путь весьма долог, и сейчас я расскажу ещё об одном эффективном методе. Идея на самом деле знакома из урока Вычисление площади с помощью определённого интеграла – это интегрирование по переменной «игрек» и использование формулы 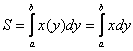 . Подставляя в неё параметрические функции  , получаем зеркальную рабочую формулу:

 

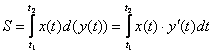
Действительно, ну а чем она хуже «стандартной»? В этом состоит ещё одно преимущество параметрической формы – уравнения   способны исполнять роль не только «обычной»  , но одновременно и обратной функции  .

В данном случае предполагается, что функции   непрерывны на промежутке интегрирования и функция   монотонна на нём. Причём, если   убывает на промежутке интегрирования (параметрические уравнения «прорисовывают» график «в противоход» (внимание!!) оси  ), то следует по уже рассмотренной технологии переставить пределы интегрирования либо изначально поставить «минус» перед интегралом.

Решение и ответ Примера №7 в конце урока.

Заключительный мини-раздел посвящен более редкой задаче: