Вычисление объема тела, образованного вращением плоской фигуры вокруг оси

Второй параграф будет еще интереснее, чем первый. Задание на вычисление объема тела вращения вокруг оси ординат – тоже достаточно частый гость в контрольных работах. Попутно будет рассмотрена задача о нахождении площади фигуры вторым способом – интегрированием по оси  , это позволит вам не только улучшить свои навыки, но и научит находить наиболее выгодный путь решения. В этом есть и практический жизненный смысл! Как с улыбкой вспоминала мой преподаватель по методике преподавания математики, многие выпускники благодарили её словами: «Нам очень помог Ваш предмет, теперь мы эффективные менеджеры и оптимально руководим персоналом». Пользуясь случаем, я тоже выражаю ей свою большую благодарность, тем более, что использую полученные знания по прямому назначению =).

Рекомендую для прочтения всем, даже полным чайникам. Более того, усвоенный материал второго параграфа окажет неоценимую помощь при вычислении двойных интегралов.

Пример 5

Дана плоская фигура, ограниченная линиями  ,  ,  .

1) Найти площадь плоской фигуры, ограниченной данными линиями. 2) Найти объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси  .

Внимание! Даже если вы хотите ознакомиться только со вторым пунктом, сначалаобязательно прочитайте первый!

Решение: Задача состоит из двух частей. Начнем с площади.

1) Выполним чертёж:

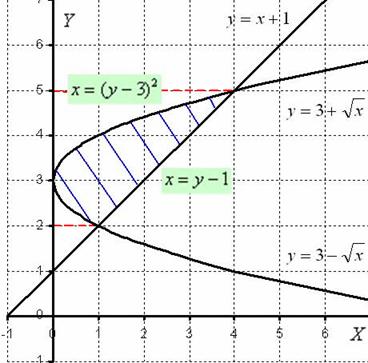
Легко заметить, что функция   задает верхнюю ветку параболы, а функция   – нижнюю ветку параболы. Перед нами тривиальная парабола, которая «лежит на боку».

Нужная фигура, площадь которой предстоит найти, заштрихована синим цветом.

Как найти площадь фигуры? Её можно найти «обычным» способом, который рассматривался на уроке Определенный интеграл. Как вычислить площадь фигуры. Причем, площадь фигуры находится как сумма площадей: – на отрезке    ; – на отрезке    .

Поэтому: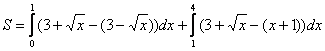 

Чем в данном случае плох обычный путь решения? Во-первых, получилось два интеграла. Во-вторых, под интегралами корни, а корни в интегралах – не подарок, к тому же можно запутаться в подстановке пределов интегрирования. На самом деле, интегралы, конечно, не убийственные, но на практике всё бывает значительно печальнее, просто я подобрал для задачи функции «получше».

Есть более рациональный путь решения: он состоит в переходе к обратным функциям и интегрированию по оси  .

Как перейти к обратным функциям? Грубо говоря, нужно выразить «икс» через «игрек». Сначала разберемся с параболой:

Этого достаточно, но убедимся, что такую же  функцию можно вывести из нижней ветки:

Для самопроверки рекомендую устно или на черновике подставить координаты  2-3-х точек параболы в уравнение  , они обязательно должны удовлетворять данному уравнению.

С прямой всё проще: 

Теперь смотрим на ось  : пожалуйста, периодически наклоняйте голову вправо на 90 градусов по ходу объяснений (это не прикол!). Нужная нам фигура лежит на отрезке  , который обозначен красным пунктиром. При этом на отрезке   прямая   расположена выше параболы  , а значит, площадь фигуры следует найти по уже знакомой вам формуле: 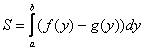 . Что поменялось в формуле? Только буква, и не более того.

! Примечание: Пределы интегрирования по оси   следует расставлять строго снизу вверх!

Находим площадь:

На отрезке    , поэтому:

Обратите внимание, как я осуществил интегрирование, это самый  рациональный способ, и в следующем пункте задания будет понятно – почему.

Для читателей, сомневающихся в корректности интегрирования, найду производные:

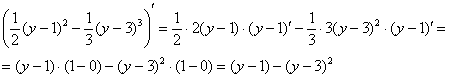
Получена исходная подынтегральная функция, значит интегрирование выполнено правильно.

Ответ: 

2) Вычислим объем тела, образованного вращением данной фигуры, вокруг оси  .

Перерисую чертеж немного в другом оформлении:

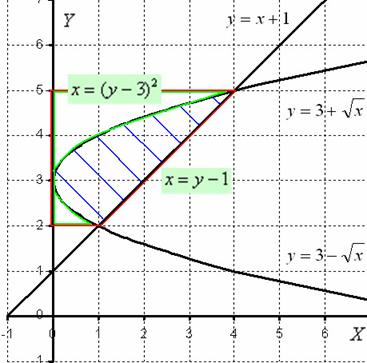
Итак, фигура, заштрихованная синим цветом, вращается вокруг оси  . В результате получается «зависшая бабочка», которая вертится вокруг своей оси.

Для нахождения объема тела вращения будем интегрировать по оси  . Сначала нужно перейти к обратным функциям. Это уже сделано и подробно расписано в предыдущем пункте.

Теперь снова наклоняем голову вправо и изучаем нашу фигуру. Очевидно, что объем тела вращения, следует найти как разность объемов.

Вращаем фигуру, обведенную красным цветом, вокруг оси  , в результате получается усеченный конус. Обозначим этот объем через  .

Вращаем фигуру, обведенную зеленым цветом, вокруг оси   и обозначаем через   объем полученного тела вращения.

Объем нашей бабочки равен разности объемов  .

Используем  формулу для нахождения объема тела вращения: 

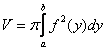
В чем отличие от формулы предыдущего параграфа? Только в букве.

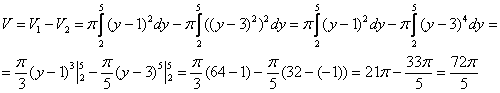
А вот и преимущество интегрирования, о котором я недавно говорил, гораздо легче найти  , чем предварительно возводить подынтегральную функцию в 4-ую степень.

Ответ: 

Однако нехилая бабочка.

Заметьте, что если эту же плоскую фигуру вращать вокруг оси  , то получится совершенно другое тело вращения, другого, естественно, объема.

Пример 6

Дана плоская фигура, ограниченная линиями  ,   и осью  .

1) Перейти к обратным функциям и найти площадь плоской фигуры, ограниченной данными линиями, интегрированием по переменной  . 2) Вычислить объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси  .

Это пример для самостоятельного решения. Желающие также могут найти площадь фигуры «обычным» способом, выполнив тем самым проверку пункта 1). А вот если, повторюсь, будете вращать плоскую фигуру вокруг оси  , то получится совершенно другое тело вращения с другим объемом, кстати, правильный ответ   (тоже для любителей порешать).

Полное же решение двух предложенных пунктов задания в конце урока.

Да, и не забывайте наклонять голову направо, чтобы разобраться в телах вращения и в пределах интегрирования!

Хотел, было уже, закончить статью, но сегодня принесли интересный пример как раз на нахождение объема тела вращения вокруг оси ординат. Свежачок:

Пример 7

Вычислить объем тела, образованного вращением вокруг оси   фигуры, ограниченной кривыми   и  .

Решение: Выполним чертеж:

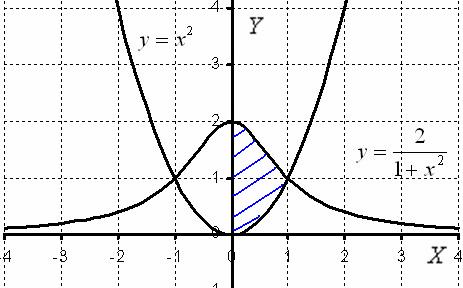
Попутно знакомимся с графиками некоторых других функций. Такой вот интересный график чётной функции  ….

Для цели нахождения объема тела вращения достаточно использовать правую половину фигуры, которую я заштриховал синим цветом. Обе функции являются четными, их графики симметричны относительно оси  , симметрична и наша фигура. Таким образом, заштрихованная правая часть, вращаясь вокруг оси  , непременно совпадёт с левой нештрихованной частью.

Перейдем к обратным функциям, то есть, выразим «иксы» через «игреки»: 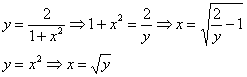Обратите внимание, что правой ветке параболы   соответствует обратная функция  . Левой неиспользуемой ветке параболы соответствует обратная функция   . В таких случаях нередко возникают сомнения, какую же функцию выбрать? Сомнения легко, развеиваются, возьмите любую точку правой ветки и подставьте ее координаты в функцию  . Координаты подошли, значит, функция   задает именно правую ветку, а не левую.

К слову, та же история и с функций  . Чайнику, не всегда бывает сразу понятно, какую обратную функцию выбрать:   или  . В действительности я и сам всегда страхуюсь, подставляя в найденную обратную функцию пару точек графика.

Теперь наклоняем голову вправо и замечаем следующую вещь:

– на отрезке   над осью   расположен график функции  ; – на отрезке   над осью   расположен график функции  ;

Логично предположить, что объем тела вращения нужно искать уже как сумму объемов тел вращений!

Используем формулу:

В данном случае:

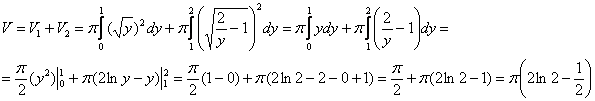
Ответ: 

В задаче нахождения площади фигуры суммирование площадей используется часто, а суммирование объемов тел вращения, видимо, редкость, раз такая разновидность чуть было не  выпала из моего поля зрения. Все-таки хорошо, что своевременно подвернулся рассмотренный пример – удалось вытащить немало полезного.

Кроме всего перечисленного, иногда линии могут быть заданы параметрически, и такие задачи тоже рассмотрены на сайте!

Успешной раскрутки фигур!

И на посошок: как найти объём тела, если оно не является телом вращения? Используемобщий принцип интегрирования.

Решения и ответы:

Пример 2: Решение: Выполним чертеж: 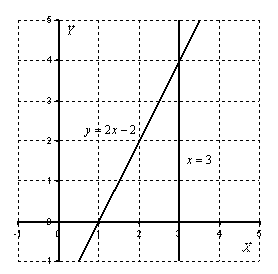Объем тела вращения: 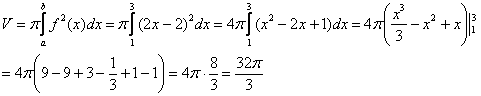Ответ: 

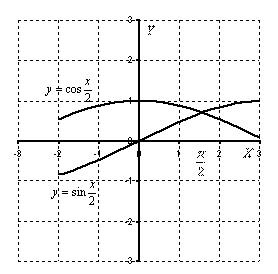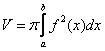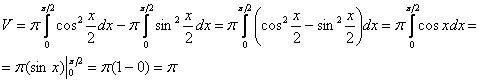Пример 4: Решение: Выполним чертеж: Объем тела вращения вычислим как разность объемов при помощи формулы: В данном случае: Ответ:  Примечание: обратите внимание на использование свойства линейности интеграла – в данном случае при интегрировании выгодно превратить два интеграла в один (это можно сделать, поскольку константы перед интегралами и пределы интегрирования одинаковы), а затем использовать формулу косинуса двойного угла.

Пример 6: Решение: 1) Выполним чертёж: 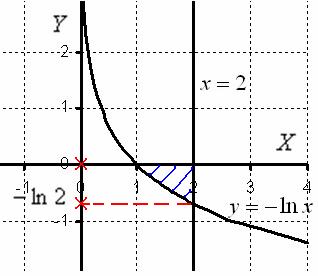Перейдем к обратной функции: На отрезке    , поэтому: 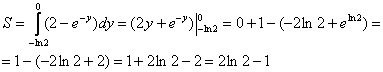Ответ: 

2) Вычислим объем тела, образованного вращением данной фигуры, вокруг оси  . Объем тела вращения найдем как разность объемов тел вращения при помощи формулы  : Ответ: 

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)