Как можно отблагодарить автора?

Числовая последовательность. Как найти предел последовательности?

На данном уроке мы узнаем много интересного из жизни участников большого сообщества под названием Вконтакте числовые последовательности. Рассматриваемая тема относится не только к курсу математического анализа, но и затрагивает основы дискретной математики. Кроме того, материал потребуется для освоения других разделов вышки, в частности, в ходе изучения числовых рядов и функциональных рядов. Можно банально сказать, что это важно, можно ободряюще сказать, что это просто, можно сказать ещё много дежурных фраз, однако сегодня первая, необыкновенно ленивая учебная неделя, поэтому меня жутко ломает сочинять первый абзац =) Уже в сердцАх сохранил файл и собрался спать, как вдруг… голову озарила идея чистосердечного признания, которое невероятно облегчило душу и подтолкнуло к дальнейшему стуку пальцами по клавиатуре.

Отвлечёмся от летних воспоминаний, и заглянем в этот увлекательный и позитивный мир новой социальной сети:

Понятие числовой последовательности

Сначала задумаемся над самим словом: а что такое последовательность? Последовательность – это когда что-то расположено за чем-то. Например, последовательность действий, последовательность времён года. Или когда кто-то расположен за кем-то. Например, последовательность людей в очереди, последовательность слонов на тропе к водопою.

Немедленно проясним характерные признаки последовательности. Во-первых, члены последовательности располагаются строго в определённом порядке. Так, если  двух человек в очереди поменять местами, то это уже будет другая последовательность. Во-вторых, каждому члену последовательности можно присвоить порядковый номер:

С числами всё аналогично. Пусть каждому натуральному значению   по некоторому правилу поставлено в соответствие действительное число  . Тогда говорят, что задана числовая последовательность  .

Да, в математических задачах в отличие от жизненных ситуаций последовательность почти всегда содержит бесконечно много чисел.

При этом:  называют первым членом последовательности;  – вторым членом последовательности;  – третьим членом последовательности; …  – энным или общим членом последовательности; …

На практике последовательность обычно задаётся формулой общего члена, например:   – последовательность положительных чётных чисел:

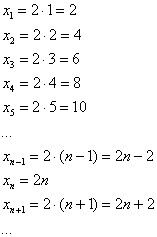
Таким образом, запись   однозначно определяет все члены последовательности – это и есть то правило (формула), по которому натуральным значениям   в соответствие ставятся числа  . Поэтому последовательность часто коротко обозначают общим членом, причём вместо «икс» могут использоваться другие латинские буквы, например:

Последовательность положительных нечётных чисел  :

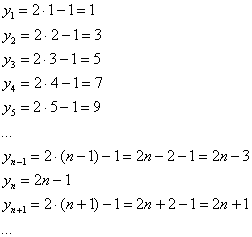
Ещё одна распространённая последовательность  :

Как, наверное, многие подметили, переменная «эн» играет роль своеобразного счётчика.

На самом деле с числовыми последовательностями мы имели дело ещё в средних классах школы. Вспомним арифметическую прогрессию. Определение переписывать не буду, коснёмся самой сути на конкретном примере. Пусть   – первый член, а   – шагарифметической прогрессии. Тогда:  – второй член данной прогрессии;  – третий член данной прогрессии;  – четвертый;  – пятый; … И, очевидно, энный член задаётся рекуррентной формулой   

Примечание: в рекуррентной формуле каждый следующий член выражается через предыдущий член или даже через целое множество предыдущих членов.

Полученная формула малопригодна на практике – чтобы добраться, скажем, до  , нужно перебрать все предыдущие члены. И в математике выведено более удобное выражение энного члена арифметической прогрессии:  . В нашем случае:

Подставьте в формулу   натуральные номера   и проверьте правильность построенной выше числовой последовательности.

Аналогичные выкладки можно провести для геометрической прогрессии, энный член которой задаётся формулой  , где   – первый член  , а   – знаменательпрогрессии  . В заданиях по матану первый член частенько равен единице.

Примеры:

прогрессия   задаёт последовательность  ; прогрессия   задаёт последовательность  ; прогрессия   задаёт последовательность  ; прогрессия   задаёт последовательность  .

Надеюсь, все знают, что –1 в нечётной степени равно  –1, а в чётной – единице.

Прогрессию называют бесконечно убывающей, если   (последние два случая).

Давайте добавим в свой список двух новых друзей, один из которых только что постучался в матрицу монитора:

Последовательность   на математическом жаргоне называют «мигалкой»: 

Таким образом, члены последовательности могут повторяться. Так, в рассмотренном примере последовательность состоит из двух бесконечно чередующихся чисел.

А бывает ли так, что последовательность состоит из одинаковых чисел? Конечно. Например,   задаёт бесконечное количество «троек». Для эстетов есть случай, когда в формуле всё же формально фигурирует «эн»: 

Факториал:    Всего лишь свёрнутая запись произведения:

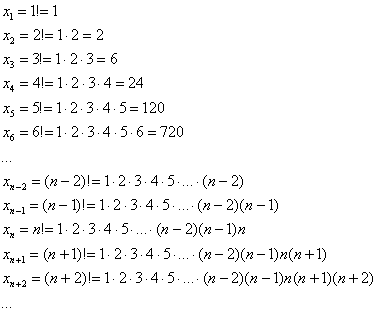
Отнюдь не графомания, пригодится для задач ;-) Рекомендую осмыслить-запомнить и даже переписать в тетрадь. …Пришёл тут в голову один вопрос: а почему никто не создаёт такие полезные граффити? Едет себе человек в поезде, смотрит в окно и изучает факториалы. Панки отдыхают =)

Возможно, некоторым читателям всё-таки ещё не до конца понятно, как расписать члены последовательности, зная общий член. Тот редкий случай, когда контрольный выстрел возвращает к жизни:

Разберёмся с последовательностью  .

Сначала подставим в энный член значение   и внимательно проведём вычисления:

Далее подставим в общий член  :

Потом подставим следующий номер  :

Четвёрку:

Чего уж, теперь и отличную отметку не зазорно заработать:

и так далее… пока разогреется самый последний чайник!