
- •Пределы функций. Примеры решений
- •1. Понять, что такое предел. 2. Научиться решать основные типы пределов.
- •1) Когда дан любой предел, сначала просто пытаемся подставить число в функцию.
- •2) Вы должны понимать и сразу решать простейшие пределы, такие как , , и т.Д.
- •Как можно отблагодарить автора?
- •Замечательные пределы. Примеры решений
- •Первый замечательный предел
- •Второй замечательный предел
- •Как можно отблагодарить автора?
- •Методы решения пределов. Неопределённости. Порядок роста функции. Метод замены
- •Что необходимо знать и уметь на данный момент?
- •Что в пределах функций является неопределённостью и не является неопределённостью
- •Порядок роста функции
- •Сравнение бесконечно больших функций
- •Если «икс» стремится к «минус бесконечности»
- •Неопределённость «бесконечность минус бесконечность»
- •Метод замены переменной в пределе
- •Устранение неопределённости «единица в степени бесконечность»
- •Как можно отблагодарить автора?
- •Бесконечно малые функции. Замечательные эквивалентности в пределах
- •Бесконечно малые функции. Сравнение бесконечно малых
- •Сравнение бесконечно малых функций
- •Что принципиально важно во всех рассмотренных примерах?
- •Систематизируем информацию о сравнении бесконечно малых функций:
- •Замечательные эквивалентности в пределах
- •Как можно отблагодарить автора?
- •Правила Лопиталя. Примеры решений
- •Первое правило Лопиталя
- •Второе правило Лопиталя
- •Вычислить предел, используя правило Лопиталя
- •Как можно отблагодарить автора?
- •Сложные пределы
- •Как можно отблагодарить автора?
- •Числовая последовательность. Как найти предел последовательности?
- •Понятие числовой последовательности
- •Понятие предела последовательности. Простейшие примеры
- •Как найти предел последовательности?
- •Как найти предел знакочередующейся последовательности?
- •Как можно отблагодарить автора?
Устранение неопределённости «единица в степени бесконечность»
Данную неопределённость «обслуживает» второй замечательный предел, и во второй части того урока мы очень подробно рассмотрели стандартные примеры решений, которые в большинстве случаев встречаются на практике. Сейчас картина с экспонентами будет завершена, кроме того, заключительные задания урока будут посвящены пределам-«обманкам», в которых КАЖЕТСЯ, что необходимо применить 2-ой замечательный предел, хотя это вовсе не так.
Недостаток двух рабочих формул 2-го замечательного предела состоит в том, что аргумент должен стремиться к «плюс бесконечности» либо к нулю. Но что делать, если аргумент стремится к другому числу?
На помощь приходит универсальная формула (которая на самом деле является следствием второго замечательного предела):
Неопределённость можно устранить по формуле:
![]()
Где-то вроде уже пояснял, что обозначают квадратные скобки. Ничего особенного, скобки как скобки. Обычно их используют, чтобы чётче выделить математическую запись.
Выделим существенные моменты формулы:
1) Речь идёт только об определённости и никакой другой.
2) Аргумент «икс» может стремиться к произвольному значению (а не только к нулю или ), в частности, к «минус бесконечности» либо к любому конечному числу.
С помощью данной формулы можно решить
все примеры урока Замечательные
пределы, которые относятся
ко 2-му замечательному пределу. Например,
вычислим предел ![]() :
:
В данном случае ![]() ,
и по формуле
,
и по формуле ![]() :
:
![]()
Правда, делать так не советую, в традициях всё-таки применять «обычное» оформление решения, если его можно применить. Однако с помощью формулы очень удобно выполнять проверку «классических» примеров на 2-ой замечательный предел.
Всё это хорошо, правильно, но сейчас в кадре более любопытные кадры:
Пример 18
Вычислить предел
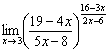
На первом шаге, не устану повторять,
подставляем значение «икс» в выражение
под знаком предела. А вдруг никакой
неопределённости вообще нет? Так бывает!
Но не в этот раз. Подставляя «тройку»,
приходим к выводу, что здесь
неопределённость ![]()
Используем формулу
Чтобы не таскать за собой букву «е» и
не мельчить, показатель ![]() удобнее
вычислить отдельно:
удобнее
вычислить отдельно:
В данном случае: ![]()
Таким образом:
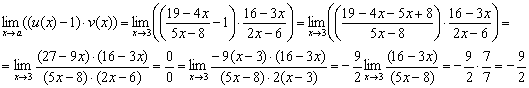
С точки зрения техники вычислений всё рутинно: сначала приводим первое слагаемое к общему знаменателю, затем выносим константы и проводим сокращения, избавляясь от неопределённости 0:0.
В результате:
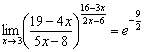
Готово.
Обещанный подарок с разностью логарифмов и неопределённостью :
Пример 19
Вычислить предел
![]()
Сначала полное решение, потом комменты:
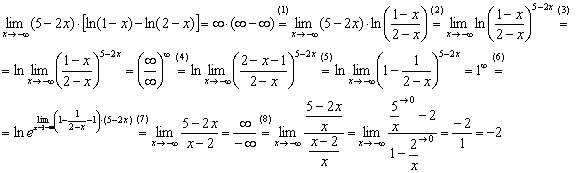
(1)-(2) На первых двух шагах используем
формулы ![]() .
У сложных
производных мы
«разваливаем» логарифмы, а здесь,
наоборот – их нужно «собрать».
.
У сложных
производных мы
«разваливаем» логарифмы, а здесь,
наоборот – их нужно «собрать».
(3) Значок предела перемещаем под логарифм. Это можно сделать, поскольку данный логарифм непрерывен на «минус бесконечности». Кроме того, предел же относится к «начинке» логарифма.
(4)-(5) Стандартным приёмом, рассмотренным
на базовом уроке про замечательные
пределы, преобразуем
неопределённость ![]() к
виду
.
к
виду
.
(6) Используем формулу .
(7) Экспоненциальная и логарифмическая
функция – взаимно обратные функции,
поэтому и «е» и логарифм можно убрать.
Действительно, согласно свойству
логарифма: ![]() .
Минус перед дробью вносим в знаменатель:
.
Минус перед дробью вносим в знаменатель: ![]()
(8) Без комментариев =) Рассмотренный тип предела не такой редкий, примеров 30-40 у себя нашёл.
Пример 20
Вычислить предел
![]()
Это пример для самостоятельного решения.
Помимо использования формулы, можно
представить предел в виде ![]() и
заменой
и
заменой ![]() свести
решение к случаю
.
свести
решение к случаю
.
В заключение рассмотрим пределы-«фальшивки».
Вернёмся к неопределённости
.
Данную неопределённость далеко
не всегда можно свести к
неопределённости
и
воспользоваться 2-ым замечательным
пределом либо формулой-следствием.
Преобразование осуществимо в том случае,
если числитель и знаменатель
основания степени – эквивалентные бесконечно
большие функции. На пример: ![]() .
.
Отвлечёмся от показателя и вычислим
предел основания:
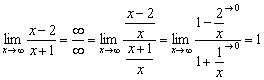
В пределе получена единица, значит, числитель и знаменатель не просто одного порядка роста, а ещё и эквивалентны. На уроке Замечательные пределы. Примеры решениймы без проблем свели данный пример к неопределённости и получили ответ.
Аналогичных пределов можно придумать
очень много:
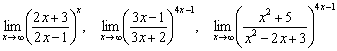 и
т.д.
и
т.д.
Дроби данных примеров объединяет
вышеуказанная особенность: ![]() .
В других случаях при
неопределённости
2-ой
замечательный предел не применим.
.
В других случаях при
неопределённости
2-ой
замечательный предел не применим.
Пример 21
Найти пределы
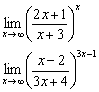
Как ни старайся, а неопределённость не удастся преобразовать в неопределённость
Здесь числители и знаменатели
оснований одного порядка роста,
но не эквиваленты: ![]() .
.
Таким образом, 2-ой замечательный предел и, тем более формулу, ПРИМЕНИТЬ НЕЛЬЗЯ.
! Примечание: не путайте с Примером №18, в котором числитель и знаменатель основания не эквивалентны. Там готовая неопределённость , здесь же речь идёт о неопределённости .
Метод решения пределов-«подделок» прост и знакОм: нужно числитель и знаменательоснования разделить на «икс» в старшей степени (невзирая на показатель):
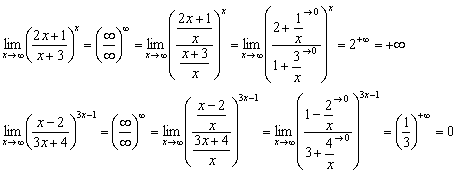
Если числитель и знаменатель основания разного порядка роста, то приём решения точно такой же:
Пример 22
Найти пределы
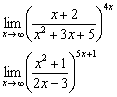
Это короткие примеры для самостоятельного изучения
Иногда неопределённости может
не быть вообще:
![]()
Подобные фокусы особенно любимы составителями сборника Кузнецова. Вот почему очень важно ВСЕГДА на первом шаге выполнять подстановку «икса» в выражение под знаком предела!
Завершая тотальное разоблачение пределов, я хочу поздравить всех посетителей сайта с новым 2013 годом! С подарком я успел, и постинг данной статьи осуществлен 31-го декабря 2012 года. Вы спросите, а как же моя личная подготовка к празднику? Давно готов =) На протяжении многих лет я занимаюсь стратегическим планированием – чтобы не толкаться в очередях до и не пересекаться с краснокожими после =)
Берегите печень!
Решения и ответы:
Пример 2
![]() Старшая
степень числителя: 2; старшая степень
знаменателя: 3.
Разделим числитель
и знаменатель на
:
Старшая
степень числителя: 2; старшая степень
знаменателя: 3.
Разделим числитель
и знаменатель на
:
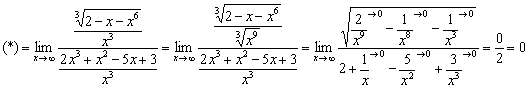
Пример 4
![]() Разделим
числитель и знаменатель на
:
Разделим
числитель и знаменатель на
:
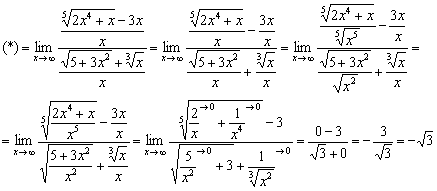 Примечание:
самым последним действием умножили
числитель и знаменатель на
Примечание:
самым последним действием умножили
числитель и знаменатель на ![]() ,
чтобы избавиться от иррациональности
в знаменателе.
,
чтобы избавиться от иррациональности
в знаменателе.
Пример 6
![]() Разделим
числитель и знаменатель на
:
Разделим
числитель и знаменатель на
:
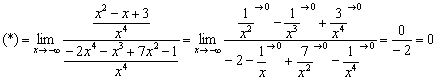
Пример 8
![]() Разделим
числитель и знаменатель на
Разделим
числитель и знаменатель на ![]() :
:
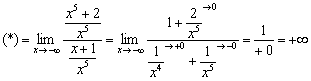 Примечание:
слагаемое
Примечание:
слагаемое ![]() стремиться
к нулю медленнее, чем
стремиться
к нулю медленнее, чем ![]() ,
поэтому
является
«главным» нулём знаменателя.
,
поэтому
является
«главным» нулём знаменателя.
Пример 10
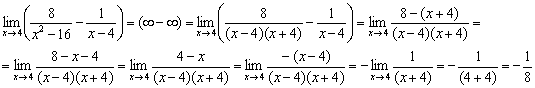
Пример 12
![]() Умножим
и разделим на сопряженное выражение:
Умножим
и разделим на сопряженное выражение:
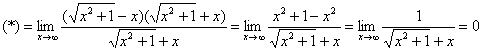
Пример 13
![]() Умножим
и разделим на сопряженное выражение:
Умножим
и разделим на сопряженное выражение:
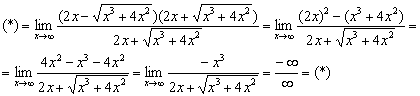 Разделим
числитель и знаменатель на
:
Разделим
числитель и знаменатель на
:
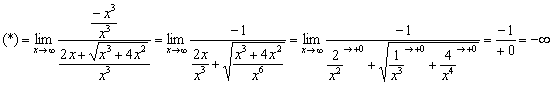
Пример 15
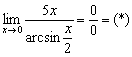 Проведём
замену:
Проведём
замену: ![]() Если
,
то
.
Если
,
то
.
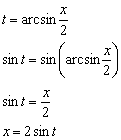
![]()
Пример 17
![]() Проведём
замену:
Проведём
замену: ![]() Если
Если ![]() ,
то
,
то ![]() .
Далее
используем формулу приведения
.
Далее
используем формулу приведения ![]() ,
тригонометрическую формулу
и
первый замечательный предел:
,
тригонометрическую формулу
и
первый замечательный предел:
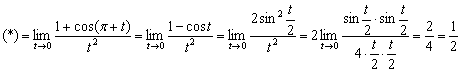
Пример 20
![]() Используем
формулу
Используем
формулу
![]()
Пример 22
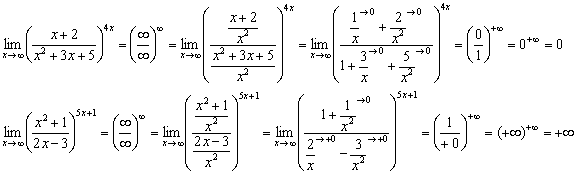 Примечание:
бесконечно малая функция
Примечание:
бесконечно малая функция ![]() стремится
к нулю медленнее, чем
стремится
к нулю медленнее, чем ![]() ,
поэтому «более большой» ноль знаменателя
играет определяющую роль:
,
поэтому «более большой» ноль знаменателя
играет определяющую роль: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)
