11. Методика вивчення письмових прийомів множення та ділення у межах тисячі.

Як відомо, до письмових прийомів відносять ті, які виконуються всіма за певним алгоритмом, із записом проміжних результатів і розпочинаються з нижчих розрядів. Характерною особливістю усних прийомів є те, що вони виконуються з вищих розрядів, без запису проміжних результатів і можуть виконуватися по-різному кожним обчислювачем.

Порядок розгляду письмових прийомів множення і ділення такий: 1) випадки множення трицифрового числа на одноцифрове без переходу через розряд, наприклад 1323, 2014; 2) прийоми письмового множення дво- або трицифрового числа на одноцифрове з одним переходом через розряд, наприклад 376, 1273, 1823; 3) випадки множення на одноцифрове число, коли у добутку з’являється один нуль, наприклад: 1415; 4) випадки множення на одноцифрове число, коли у добутку з’являється два нулі,наприклад: 1254; 5) випадки письмового ділення трицифрового числа на одноцифрове число, коли всі неповні ділені одноцифрові, та частка містить три цифри, наприклад: 936:3; 6) випадки ділення трицифрового числа на одноцифрове, коли одне з неповних ділених двоцифрове, та у частці отримуємо трицифрове число, наприклад: 864:4; 7) прийоми письмового ділення трицифрового числа на одноцифрове, коли всі неповні ділені двоцифрові, та у частці одержуємо двоцифрове число, наприклад: 276:4; 8) випадки ділення трицифрового числа на одноцифрове, коли є одноцифрові та двоцифрові неповні ділені, та частка трицифрове число, наприклад 875:5; 9) випадки ділення трицифрового числа на одноцифрове, коли ділене містить нулі, наприклад 370:2, 804:3.

Випадки множення трицифрового числа на одноцифрове без переходу через розряд, наприклад 1323. Спочатку пропонуємо учням усно обчислити цей приклад, користуючись правилом множення суми на число, розкладаючи перший множник на розрядні доданки:

1323=(100+30+2) 3=1003+303+23=300+90+6=396

1323=132+132+132=396

З’ясувавши, що так не зручно обчислювати кажемо, що в математиці існує письмове множення і пояснюємо, як правильно записувати числа при письмовому множенні. Записуємо множники один під одним, але другий множник записуємо під одиницями першого.

1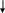 32

3

396

Алгоритм детального пояснення для випадку множення:

2од. помножити на 3 дорівнює 6од. Цифру 6 підписуємо під одиницями.

3 дес. помножити на 3 дорівнює 9дес. Цифру 9 підписуємо під десятками.

1сот. Помножити на 3 дорівнює 3сот. Цифру 3 підписуємо під сотнями.

У добутку дістали 396.

127

3

381

Випадки множення трицифрового числа на одноцифрове з одним переходом через розряд.

Алгоритм детального пояснення для випадку множення:

7од. помножити на 3 дорівнює 21од. Це 2дес і 1 од. Цифру 1 підписуємо під одиницями, а 2дес. додамо до добутку десятків.

2дес. помножити на 3 дорівнює 6дес. та ще 2 дес. буде 8дес. Цифру 8 підписуємо під десятками.

1сот. помножити на 3 дорівнює 3сот. Цифру 3 підписуємо під сотнями.

У добутку дістали 381.

Коли учні засвоять алгоритми детального пояснення, вчитель подає алгоритм короткого пояснення:

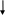237

4

948

7 на 4 буде 28. 8 пишемо під одиницями, 2 додамо до добутку десятків.

3 на 4 буде 12, та ще 2 буде 14. 4 пишемо під десятками, 1 додамо до наступного добутку.

2 на 4 буде 8, та ще 1 буде 9. 9 пишемо під сотнями.

У добутку дістали 948.

Найскладнішим у школі є алгоритм письмового ділення.

Підготовчими вправами до розгляду випадків письмового ділення багатоцифрових чисел на одноцифрове вважають: 1) розв'язування прикладів на ділення однозначного числа на однозначне з остачею; 2) двозначного на однозначне з остачею. У кожному з названих випадків учні повинні говорити не остача не ділиться на дільник, а остача менша ніж дільник. 3) ґрунтовне повторення нумерації багатоцифрових чисел (класи та розряди); 4) розв'язування прикладів на округлення числа до бажаного розряду, але для округлення до десятків краще брати двозначні числа.

Випадки письмового ділення трицифрового числа на одноцифрове число, коли всі неповні ділені одноцифрові, якщо частка містить три цифри, наприклад: 936.

Спочатку пропонуємо учням усно обчислити цей приклад, користуючись правилом ділення суми на число, розкладаючи ділене на розрядні доданки:

936:3=(900+30+6):3=900:3+30:3+6:3=300+10+2=312

З’ясувавши, що так не зручно обчислювати кажемо, що в математиці існує письмове ділення і пояснюємо, як правильно записувати числа при письмовому діленні.

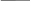_ 936|3

9 312

_3

3

_6

6

0

Алгоритм детального пояснення для випадку ділення:

Утворюємо перше неповне ділене. Перше неповне ділене 9сот.

Визначаємо скільки цифр буде у частці .Отже, у частці буде 3 цифри: сотні, десятки, одиниці (ставлю три точки у частку).

Знаходимо першу цифру частки: 9сот. : 3 = 3сот. Записуємо в частку на місці сотень цифру 3.

Перевіряємо скільки сотень поділилось: 3сот.3=9сот. Підписую 9 під першим неповним діленим і віднімаю: 9сот.-9сот.=0сот. Всі сотні поділились. Цифра підібрана правильно.

Утворюємо друге неповне ділене: це 3дес.

Знаходимо другу цифру в частці: 3дес.:3=1дес. Записуємо в частку на місці десятків цифру1.

Перевіряємо скільки десятків поділилось: 1дес.3 =3дес. Підписую 3 під другим неповним діленим і віднімаю: 3дес.-3дес.=0дес. Всі десятки поділились. Цифра підібрана правильно.

Утворюємо третє неповне ділене: це 6од.

Знаходимо третю цифру частки: 6од.: 3 =2од. Записуємо в частку на місці одиниць цифру 2.

Перевіряємо скільки одиниць поділилось:2од.3=6од. Підписую 6 під третім неповним діленим і віднімаю: 6од.-6од.=0од. Всі одиниці поділились. Цифра підібрана правильно.

У частці отримали 312.

Прийоми письмового ділення трицифрового числа на одноцифрове, коли всі неповні ділені двоцифрові, та у частці одержуємо двоцифрове число, наприклад: 276:4.

276|4

24 69

36

36

0

Алгоритм скороченого пояснення для випадку ділення:

Утворюємо перше неповне ділене. 2сот. не можна поділити на 4, щоб одержати сотні. 2сот. та ще 7дес. – буде 27дес. Тому перше неповне ділене – 27 дес. Отже, у частці буде 2 цифри (ставлю 2 точки). Знаходимо першу цифру в частці, для цього потрібно: 27:4, беремо по 6. Перевіряємо скільки десятків поділилось. Для цього 64=24. Записуємо 24 під першим неповним діленим ( або під десятками) і віднімаю: 27-24=3. 3дес. – не поділилось. 3 менше, ніж 4. Отже, перша цифра частки підібрана правильно.

Утворюємо друге неповне ділене: 3дес. – це 30од. та ще 6од. буде 36од. Знаходимо другу цифру в частці, для цього потрібно: 36:4, беремо по 9. Перевіряємо скільки одиниць поділилось. Для цього 94=36.Записую 36 під другим неповним діленим і віднімаю: 36-36=0. Всі одиниці поділились.

У частці отримали 69.

Зазначимо, що скорочення пояснень слід проводити поступово у відповідності з індивідуальними особливостями сприймання і засвоєння алгоритму. Основна робота з формування прийому письмового алгоритму ділення на одноцифрове число відбуватиметься у наступному концентрі, що є одним з недоліків програми і підручника, адже за літо діти ґрунтовно забудуть алгоритм.