
- •2 . Двоичная система счисления — это позиционная система счисления с основанием 2. Для записи чисел в двоичной системе используются всего две цифры (0 и 1).
- •Основные сведения[править | править исходный текст]
- •Основные параметры интегральных схем
- •Разновидности
- •Принцип действия
- •Ключевой с широтно-импульсной модуляцией
- •Ключевой с триггером Шмитта
- •Достоинства вторичных источников питания с импульсной стабилизацией
- •Недостатки
- •Комбинационные цифровые устройства
- •Мультиплексоры и демультиплексоры.
- •Последовательностные цифровые устройства (пцу)
- •Триггеры
- •Принцип работы и разновидности триггеров
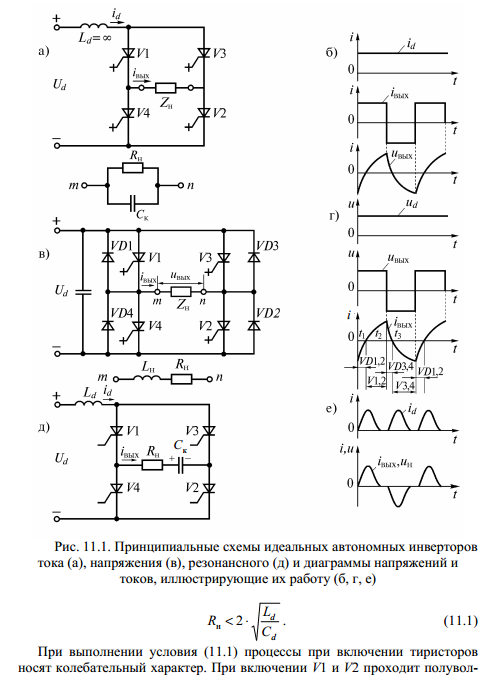
- •19. Управляемые выпрямители
- •Коэффициент сглаживания[править | править исходный текст]
- •Виды сглаживающих фильтров[править | править исходный текст] Индуктивный сглаживающий фильтр[править | править исходный текст]
- •Емкостной сглаживающий фильтр[править | править исходный текст]
- •Трехфазная мостовая схема выпрямителя
Оглавление
1. 2
2 . Двоичная система счисления — это позиционная система счисления с основанием 2. Для записи чисел в двоичной системе используются всего две цифры (0 и 1). 4
Определение[править | править исходный текст] 4
Основные сведения[править | править исходный текст] 5
Таблицы истинности[править | править исходный текст] 6
Аксиомы[править | править исходный текст] 6
Логические операции 7
Свойства логических операций[ 7
3. 9
4. 11
Основные параметры интегральных схем 14
5 18
6. 25
7. 28
8. 30
9. 32
10. 34
11. 35
Разновидности 36
Принцип действия 36
Ключевой с широтно-импульсной модуляцией 37
Ключевой с триггером Шмитта 38
Достоинства вторичных источников питания с импульсной стабилизацией 38
Недостатки 39
12. 40
Комбинационные цифровые устройства 40
Сумматоры 40
Сумматоры — это комбинационные устройства, предназначенные для сложения двух входных двоичных кодов. Например, арифметическая сумма кодов 0111 (число 7) и 0101 (число 5) равна 1100 (число 12). Арифметическая сумма кодов 1101 (число 13) и 0110 (число 6) равна 10011 (число 19), т. е. сумма двух двоичных чисел с числом разрядов n может иметь результат с числом разрядов n + 1. Этот дополнительный (старший) разряд называется выходом переноса (Р). На схемах сумматоры обозначаются буквами SM. Микросхемы сумматоров кодируются буквами ИМ. Рассмотрим таблицу истинности сложения двух одноразрядных двоичных чисел без учёта переноса: 40
13. 45
14. 47
Мультиплексоры и демультиплексоры. 48
15. Параметрический стабилизатор напряжения - это устройство, в котором стабилизация выходного напряжения достигается за счет сильной нелинейности вольт-амперной характеристики электронных компонентов, использованных для построения стабилизатора (т.е. за счет внутренних свойств электронных компонентов, без построения специальной системы регулирования напряжения). 52
Основные характеристики стабилитрона 54
Токи и напряжения стабилизации, Дифференциальное сопротивление, Температурный коэффициент напряжения, Дрейф и шум, Динамические характеристики, Область безопасной работы, Характер и причины отказов 54
16. 54
Последовательностные цифровые устройства (ПЦУ) 54
Триггеры 54
17. 57
18. 59
19. Управляемые выпрямители 62
20. 64
21. 68
Коэффициент сглаживания[править | править исходный текст] 69
Виды сглаживающих фильтров[править | править исходный текст] 69
Индуктивный сглаживающий фильтр[править | править исходный текст] 69
Емкостной сглаживающий фильтр[править | править исходный текст] 70
22. D-триггер (от английского DELAY) называют информационным триггером, также триггером задержки. D - триггер бывает только синхронным. Он может управляться (переключаться) как уровнем тактирующего импульса, так и его фронтом. Для триггера типа D, состояние в интервале времени между сигналом на входной линии и следующим состоянием триггера формируется проще, чем для любого другого типа. 71
23. 76
Трехфазная мостовая схема выпрямителя 76
24. 79
25. 83
1.


2 . Двоичная система счисления — это позиционная система счисления с основанием 2. Для записи чисел в двоичной системе используются всего две цифры (0 и 1).
Такие сигналы легко задать определенными уровнями напряжения в электронных схемах. Например 0 вольт — отсутствие напряжения можно считать логическим нулём, а напряжение в 5 вольт принять за единицу.
Выставляя различные уровни, можно осуществлять передачу данных в виде последовательностей нулей и единиц, а также реализовать ее обработку и хранение. На графике процесс передачи таких данных по одной линии (проводу) можно изобразить так:
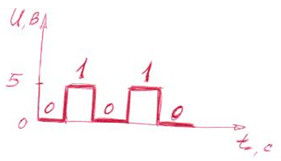
Именно так выглядят протоколы предачи данных различных цифровых устройств, разумеется в действительности они более сложны, поскольку содержат не одну линию
Алгебра логики (алгебра высказываний) — раздел математической логики, в котором изучаются логические операции над высказываниями[1]. Чаще всего предполагается, что высказывания могут быть только истинными или ложными, то есть используется так называемая бинарная или двоичная логика, в отличие от, например, троичной логики
Определение[править | править исходный текст]
Базовыми элементами, которыми оперирует алгебра логики, являются высказывания.
Высказывания
строятся над множеством {B, ![]() ,
, ![]() ,
, ![]() ,
0, 1}, где B — непустое множество, над
элементами которого определены
три операции:
,
0, 1}, где B — непустое множество, над
элементами которого определены
три операции:
отрицание (унарная операция),
конъюнкция (бинарная),
дизъюнкция (бинарная),
а логический ноль 0 и логическая единица 1 — константы.
Так же используются названия
Дизъю́нкт — пропозициональная формула, являющаяся дизъюнкцией одного или более литералов (например
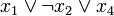 ).
).Конъюнкт — пропозициональная формула, являющаяся конъюнкцией одного или более литералов (например
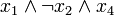 ).
).
Унарная
операция отрицания в тексте формул
оформляется либо в виде значка перед
операндом (![]() )
либо в виде черты над операндом (
)
либо в виде черты над операндом (![]() ),
что компактнее, но в целом менее заметно.
),
что компактнее, но в целом менее заметно.
Бу́лева фу́нкция (или логи́ческая функция, или функция а́лгебры ло́гики)[1] от n аргументов — в дискретной математике — отображение Bn → B, где B = {0,1} — булево множество. Элементы булева множества {1, 0} обычно интерпретируют как логические значения «истинно» и «ложно», хотя в общем случае они рассматриваются как формальные символы, не несущие определённого смысла. Неотрицательное целое число n называют арностью или местностью функции, в случае n = 0 булева функция превращается в булеву константу. Элементы декартова произведения (n-я прямая степень) Bn называют булевыми векторами. Множество всех булевых функций от любого числа аргументов часто обозначается P2, а от n аргументов — P2(n). Переменные, принимающие значения из булева множества называются булевыми переменными[2]. Булевы функции названы по фамилии математика Джорджа Буля.
При работе с булевыми функциями происходит полное абстрагирование от содержательного смысла, который имелся в виду в алгебре высказываний[2]. Тем не менее, между булевыми функциями и формулами алгебры высказываний можно установить взаимно-однозначное соответствие, если[3]:
установить взаимно-однозначное соответствие между булевыми переменными и пропозициональными переменными,
установить связь между булевыми функциями и логическими связками,
оставить расстановку скобок без изменений
